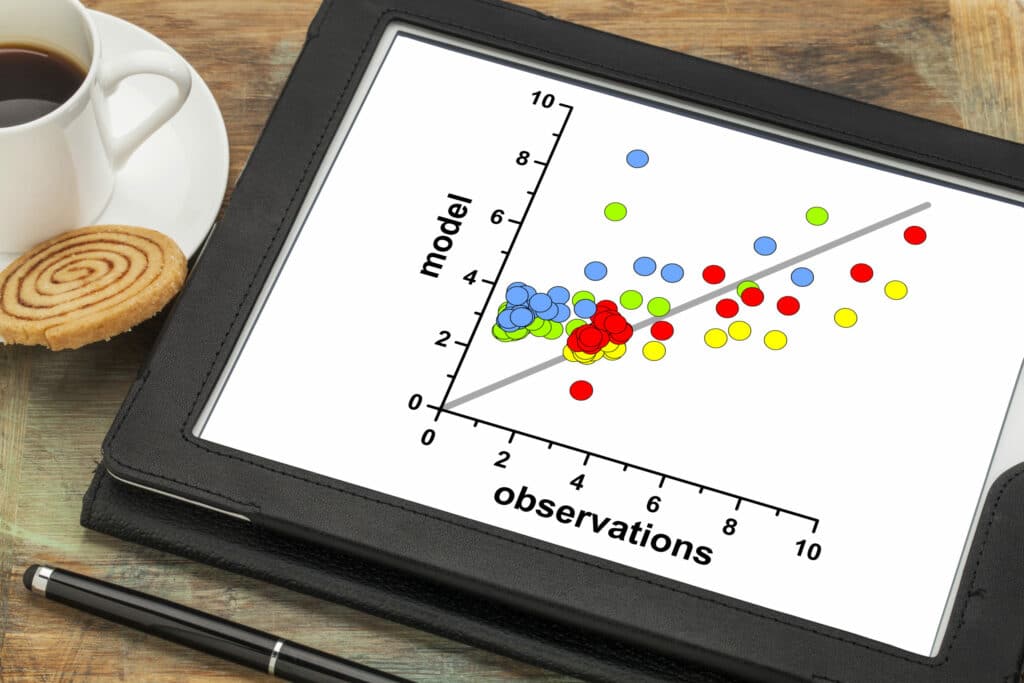
La visualisation des données dans le monde de la data science est de nos jours au cœur de la pipeline du machine learning. La data visualization est ainsi l'une des étapes de la science des données, qui intervient juste après la collecte, le nettoyage et la normalisation des données. De nos jours, l’un des graphiques les plus utilisés est le scatter plot. Ce dernier nous permet d'analyser les données et voir les interactions entre les variables.
Un Scatter Plot, c’est quoi ?
Nommé également scattergram, scatter graph ou aussi scatter chart, les scatter plots sont un type de graphique sous forme d’un nuage de points montrant ainsi comment une variable est affectée par une autre. L’axe vertical, ou l’axe des ordonnées est utilisé pour afficher l’une des variables et un axe horizontal, ou l’axe des abscisses pour l’autre variable.
Contrairement aux pie charts qui sont plutôt adaptés pour les variables catégorielles, les scatter plots sont souvent utilisés pour représenter une corrélation entre variables quantitatives qui semblent être liées. Par exemple, la température moyenne d’une journée peut affecter le nombre de bouteilles d’eau fraîche vendues dans un supermarché.
Ainsi, en représentant ces points, on pourra déduire si la relation entre la température moyenne d’une journée et le nombre de bouteilles d’eau fraîche vendues est plutôt linéaire ou non-linéaire, forte ou faible, ou encore positive ou négative.
Quelles sont les applications du Scatter Plot ?
1. Analyser les relationships between variables
- Relation forte / faible
On évalue la force d’un scatter plot par la dispersion de ses points. En effet, si les points sont très dispersés, la relation entre les variables est faible. Si les points sont concentrés autour d’une droite, la relation entre les variables est forte.
- Relation positive / négative
Une composante importante d’un nuage de points est la direction de la relation entre les variables. On appelle une corrélation positive, lorsque les coordonnées x et y augmentent en même temps. Si vous regardez l’âge d’un enfant et sa taille, vous constaterez que plus l’enfant vieillit, plus il grandit aussi. Il s’agit d’une relation positive entre les variables.
Dans le cas contraire, si les valeurs de l’axe x augmentent et les valeurs de l’axe y diminuent (ou inversement), on pourra alors déduire que la relation est négative. Par exemple, si vous regardez l’âge d’une voiture et sa valeur, vous constaterez que plus la voiture vieillit, moins elle a de valeur. Il s’agit d’une corrélation négative.
- Relation Linéaire / non-linéaire
La forme du nuage des points nous permet de déduire la linéarité des données. Ainsi, si le nuage des points ressemble étroitement à une ligne droite, la relation est linéaire. On peut alors en déduire qu’une variable augmente à peu près au même rythme lorsque l’autre variable change d’une unité. Dans le cas où le scatter plot est sous la forme d’une courbe ou autre, la relation se dit non linéaire entre les variables.
2. Identifier des clusters et des outliers
Avant toute chose, définissons les clusters et les outliers.
- Cluster
Un cluster en data science est une sous-population d’un ensemble de données plus large dans lequel chaque point de données est plus proche d’un centroïde (centre d’un cluster) que des centroïdes dans l’ensemble de données. Le clustering reste l’une des méthodes les plus utilisées dans l’apprentissage non supervisé. Il peut être utilisé pour plusieurs applications, y compris la segmentation de clients, l’analyse des réseaux sociaux ou encore les systèmes de recommandation.
- Outlier
Un outlier en science des données est une observation qui diffère des autres observations. Lors de la collecte des données, il arrive parfois que l’ensemble de données peut contenir des valeurs extrêmes qui se situent en dehors de l’intervalle de données attendues. Ces valeurs sont appelées valeurs aberrantes.
Contrairement aux pie charts qui ne nous permettent pas d’identifier les clusters et outliers, les scatter plots nous permettent de mieux analyser nos données en vue de lancer le preprocessing adapté, et choisir l’algorithme de machine learning le plus convenable à notre problème.
3. Appliquer une Regression Linear
Les modèles de régression étudient la relation entre une variable dépendante (cible) et une ou plusieurs variables indépendantes (prédicteur). Voici quelques modèles de régression les plus courants:
- Régression linéar: Ayant la forme d’une ligne droite, la régression linéaire permet d’établir une relation linéaire entre la cible (Y) et le prédicteur (X)
- Régression Polynomial: Ayant la forme d’une courbe, la régression polynomiale permet d’établir une relation non linéaire entre la cible (Y) et le prédicteur (X)
Malgré sa simplicité, la régression linéaire est un outil incroyablement puissant pour analyser des données ayant une forme linéaire. Cet algorithme fait partie de la famille des algorithmes de machine learning supervisés.
Une régression linéaire a comme équation y = mx+b. La variable x est appelée variable indépendante ou explicative. La variable y est appelée la variable dépendante ou variable à expliquer.
Les scatter plots sont ainsi facilement complétés par une simple régression linéaire en calculant nos paramètres m et b afin de placer une droite de régression à travers nos données. Ce calcul des paramètres se fait au travers des relations suivantes:

L’équation de la régression linéaire garantit alors que la distance entre chaque point de données et la droite de régression est minimisée. Cependant, il faudra vérifier les points suivants:
- La relation entre les données doit être linéaire : le nuages des points doit former une ligne droite plutôt qu’une courbe ou toute autre forme.
- L’hypothèse d’additivité doit être vérifiée. Cela signifie que le changement dans une des features de la variable cible ne dépend pas des valeurs des autres features. Prenons comme exemple, un modèle de prévision du chiffre d’affaires d’une entreprise comportant deux caractéristiques : le nombre de stylos et le nombre de cahiers vendus. Lorsque l’entreprise vend plus de stylos, le chiffre d’affaires des stylos augmente, et cela est indépendant du nombre de cahiers vendus. Cependant, si les clients qui achètent des stylos cessent d’acheter les cahiers, l’hypothèse d’additivité n’est plus vérifiée, car dans ce cas le chiffre d’affaires produit par les cahiers est dépendant par l’achat des stylos.
- Les features ne doivent pas être corrélées. C’est à dire que les observations de la variable cible ne sont pas liées avec les précédentes et n’influent pas les suivantes.
- Les erreurs sont indépendamment et identiquement distribuées selon la loi normale.
Quels sont les problèmes avec les Scatter Plots ?
1. Données non corrélées
Dans le cas où on n’a pas de corrélations ni de liens entre nos données, les points de données sont dispersés un peu partout et aucune interprétation ne peut être déduite. En d’autres termes, le fait de connaître la valeur d’une variable ne nous donne aucune idée de ce que peut être la valeur de l’autre variable. Si nous avons un scatter plot de deux variables dont la corrélation est nulle, le graphique ne présentera aucune tendance claire. Par exemple, la corrélation entre la quantité de café consommée par un individu et son niveau de QI est nulle. En d’autres termes, savoir combien de café un individu boit ne nous donne pas une idée de son niveau de QI.
2. Quantité de données importante
Dans le cas de grands ensembles de données, les points du scatter plot peuvent se chevaucher et se masquer mutuellement. Appelé overplotting, ce dernier masque les tendances et les relations entre nos deux variables et rend l’analyse difficile. Il existe ainsi différentes solutions à ce problème:
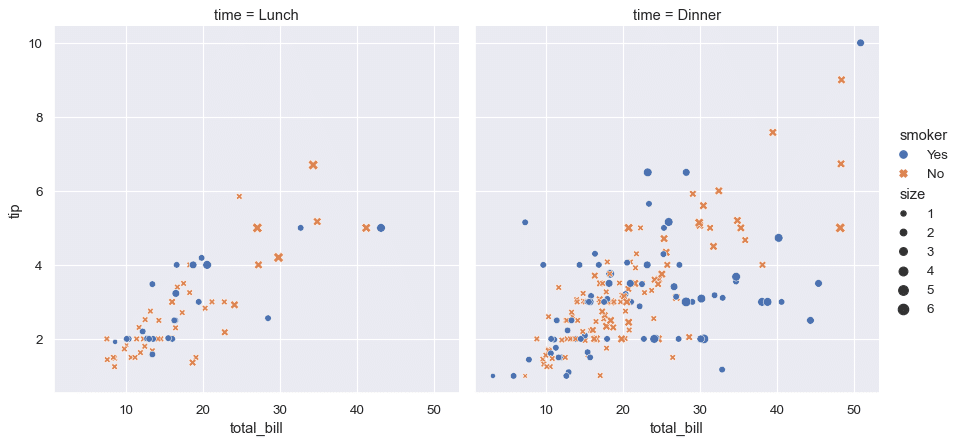
- Supprimer la couleur de remplissage des points représentants nos données ou réduire leurs tailles permet de rendre le plot plus facile à analyser et montre la façon dont les points se chevauchent.
- Une autre technique simple qui s’avère souvent utile consiste à modifier la forme des points de données qui prennent assez d’espace comme par exemple les cercles ou carré en une forme qui ne prend pas trop d’espace comme les croix par exemple.
- Réduire le nombre d’observations est souvent utilisé aussi. Pour ce faire, il existe 2 méthodes:
- Filtrer les données: Ils s’agit simplement de supprimer les données dont on ne peut pas s’en servir dans le but de réduire le nombre de données et améliorer la lisibilité
- Répartir les données en plusieurs graphes peut s’avérer aussi une bonne solution si on ne veut pas perdre de l’information.
Pour conclure, les pie charts peuvent être une excellente alternative dans le cas des variables catégorielles. Ainsi, il existe différentes librairies pour l’analyse et la visualisation des données avec Python, comme par exemple Matplotlib, Seaborn ou encore Plotly !
Prêt à tracer votre scatter plot ? Apprenez davantage sur l’analyse et la visualisation des scatter plots ainsi que d’autres graphiques de visualisation de données sur Datascientest.