Desde la estadística que estudia el movimiento de los cuerpos, hasta la variación de las acciones financieras en bolsa, las funciones se utilizan en todos los campos. Cada vez que presionamos una tecla del teclado de una computadora o que utilizamos nuestro móvil, detrás se desencadenan múltiples funciones sucesivas que producen transformaciones hasta generar un resultado.
En este artículo te presentamos algunos puntos claves para entender lo que son las funciones :
1. La definición de una función y algunos ejemplos :
Una función, en matemática, permite definir un resultado asociado a un valor que pertenece a un dominio de entrada. El resultado se puede obtener mediante varias operaciones aritméticas, con procedimientos diferentes (como resolver una ecuación o calcular los límites).
Un ejemplo de definición formal de función puede ser la siguiente :
“Una función f es una manera de asociar a todo número real X un solo número real Y.”
En esta definición, se debe tener en cuenta que:
- X corresponde a la variable de la función (en los casos de funciones de una sola variable)
- Y corresponde a la imagen de la variable X para f (se escribe “imagen de una función f(x) o y=f(x) ).
Algunos ejemplos de formas de asociar un número a otro son:
- Mediante una función matemática (por ejemplo: f(x) = 4x + 10)
- Mediante una curva (por ejemplo una curva que muestra la evolución de la temperatura con respecto al tiempo).
- Mediante un instrumento de medida (por ejemplo un medidor de electricidad)
- Mediante una tabla de valores que indique la correspondencia entre 2 líneas de valores.
El cálculo de un resultado se puede realizar por medio de funciones informáticas que efectúen operaciones sobre los datos de entrada. La función informática consiste entonces en la descripción del método para obtener un resultado a partir de ciertos parámetros dados de entrada (esto es conocido como algoritmo).
En la teoría de conjuntos, una función puede ser definida como la relación entre dos conjuntos en los que, a cada elemento de un conjunto inicial, corresponden uno o varios elementos de un conjunto final.
2. Principio general y ejemplos de funciones.
Si consideramos 2 conjuntos de números (un conjunto inicial y uno final como en la siguiente imagen) :
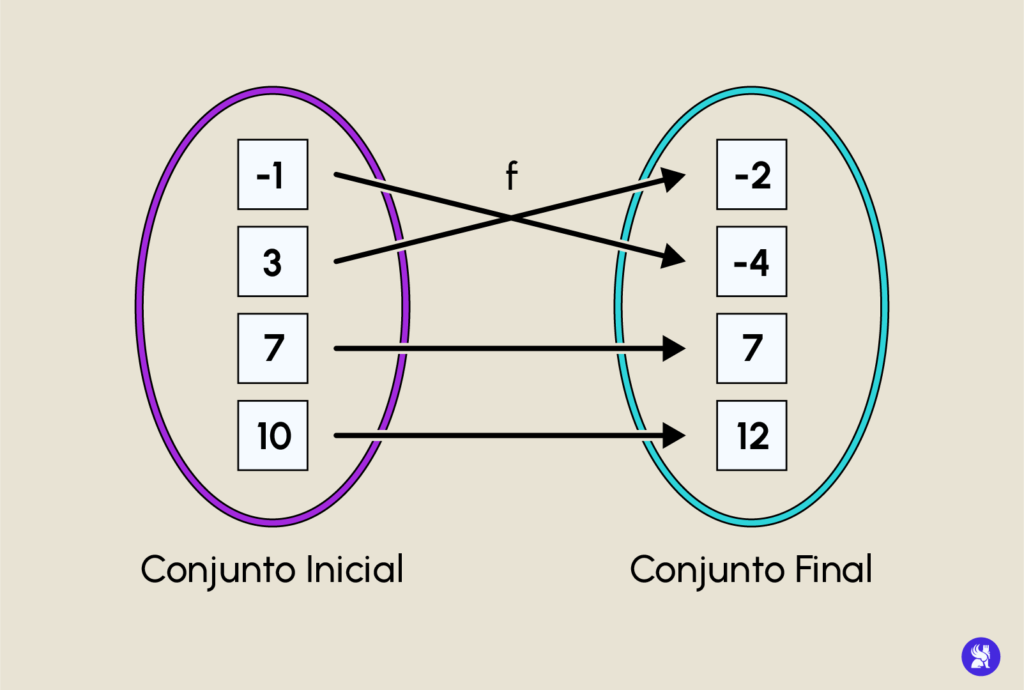
La correspondencia entre los dos conjuntos se asegura mediante la función f (que podría tener un nombre distinto de f). Basándonos en esta representación, se puede ver con claridad que f podría ser reemplazada por la siguiente tabla :
Para completar la interpretación, todos los números del conjunto final son llamados las “imágenes” de los números del conjunto inicial, y los números del conjunto inicial son llamados los “antecedentes” de los números del conjunto final.
Para definir de manera rigurosa una función en matemática, en la práctica, se necesitan definir sus diferentes propiedades, es decir su regularidad, sus variaciones, su integrabilidad, etc.
Para ello, existen diferentes tipos de funciones, entre las que podemos mencionar:
- Las funciones constantes, aquellas que asocian siempre un mismo resultado a un conjunto de valores (por ejemplo f(x) = 5).
- Las funciones lineares, aquellas que siempre se expresan como f(x) = ax + b (a siendo siempre un número)
- Las funciones afinadas, aquellas utilizadas en varios algoritmos de Machine Learning, que expresan f(x) = ax + b (a y b siendo siempre números).
3. Conjuntos de definiciones de una función
El conjunto de definiciones de una función f es el conjunto de todos los números del conjunto inicial que poseen una imagen para la aplicación de f.
Por ejemplo, el dominio de definición de la función de una variable f(x) = 1/x es D = (-, 0) U (0, +), 0 siendo excluido ya que la división por 0 es imposible.
La definición de una función puede entonces realizarse de la siguiente manera :
f : D→R
X→f(x)
Esta definición muestra claramente que la correspondencia entre los elementos D que tiene una imagen f(x) en R (en este caso dentro de los números reales).
4. Representación gráfica de una función
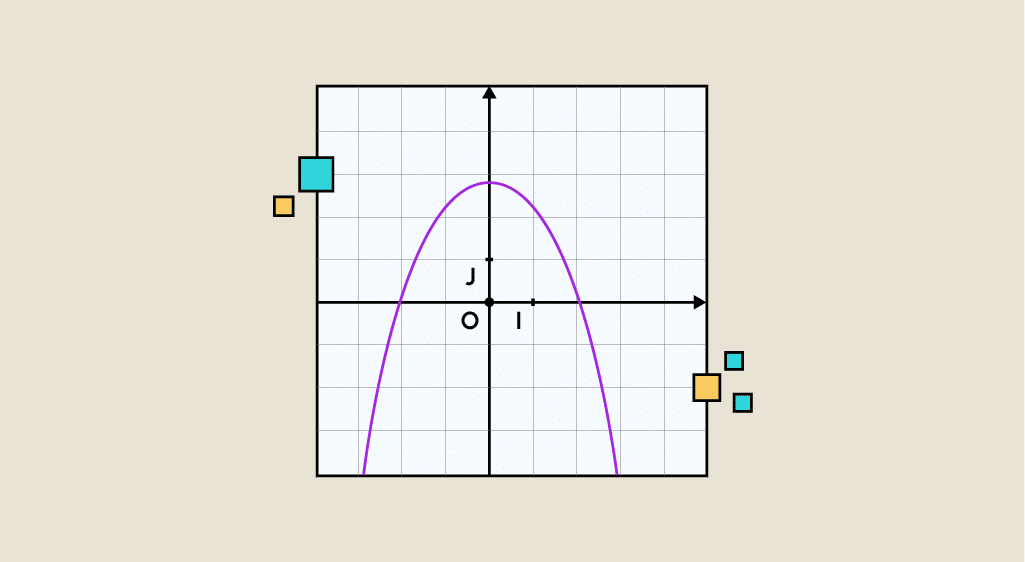
La representación gráfica de una función corresponde a la representación visual de esta en un espacio fijado como marco. En dos dimensiones, se utiliza frecuentemente un espacio ortonormal (O, I, J), que corresponde a un espacio en el que los puntos O, I y J forman un triángulo rectángulo isósceles en O (O siendo el origen del marco).
Las rectas OI y OJ representan respectivamente los ejes de abscisas y ordenadas.

Siendo F una función y D el conjunto de definición asociado. En un marco de referencia ortonormal u ortogonal (O, I, J), el conjunto de puntos M de coordenadas (x, f(x)) donde x describe un dominio de D (también llamado intervalo I), se llama curva representativa o de representación gráfica (Cf) de la función f. Así, se dice que Cf (la curva representativa de la función) tiene por ecuación y = f(x).
Por otro lado, el eje de las abscisas (horizontal) representa los antecedentes (es decir las x) y el eje vertical representa las imágenes (las f(x)).
En el ejemplo anterior, si f(-1) = -4, esto significa que Cf pasa por el punto de coordenadas (-1, -4). De esta manera, Cf describe el conjunto de puntos que respetan la ecuación y = f(x).
5. Noción de variación y extremums de una función
La variación de una función es una propiedad que se estudia sistemáticamente.
Tomemos una función f definida sobre un intervalo I. Existen varias posibilidades en términos de variación de la función f sobre I.
- f puede ser creciente: se dice que f es creciente sobre I si por cada x y x’ en I se verifica : si x < x’ entonces f(x) f(x’).
- f puede ser estrictamente creciente : se dice que f es estrictamente creciente sobre I si por cada x y x’ en I se verifica : si x < x’ entonces f(x) f(x’).
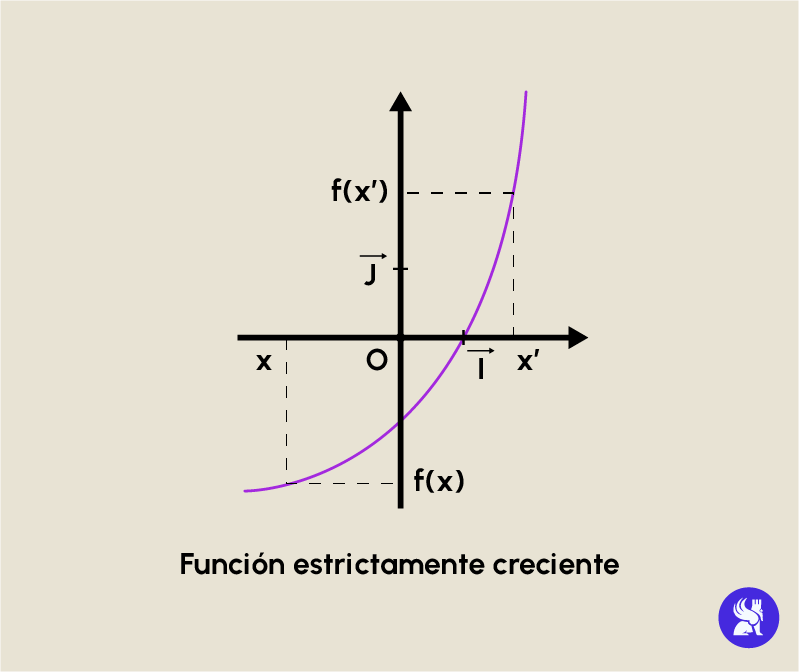
- f puede ser decreciente : se dice que f es decreciente sobre I si por cada x y x’ se verifica: si x < x’ entonces f(x) f(x’).
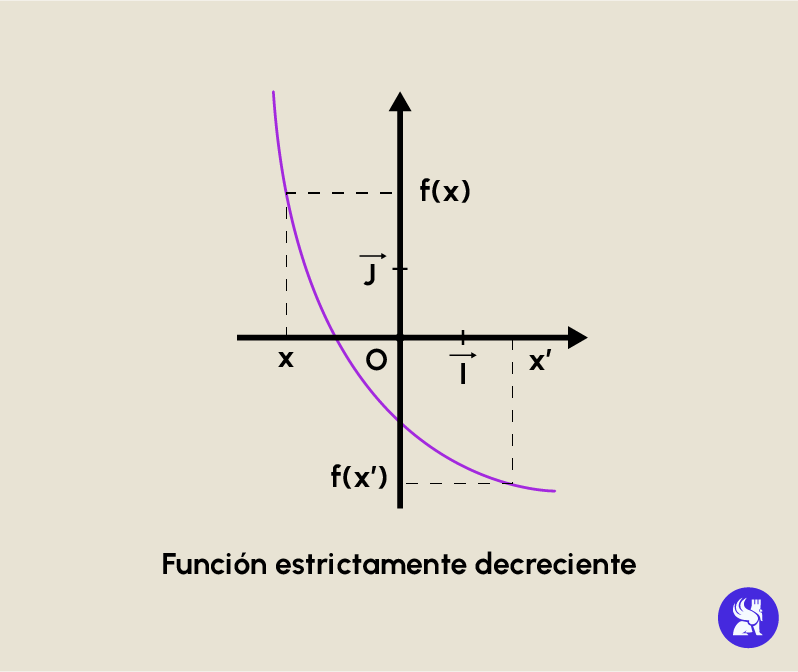
- f puede ser estrictamente decreciente : se dice que f es estrictamente decreciente sobre I si por toda x y x’ se verifica: si x < x’ entonces f(x) f(x’).
- f puede ser constante: se dice que f es constante si existe una constante D tal que para toda x en I se tenga f(x) = d.
- f puede ser monótona: se dice que f es monótona (o exclusiva) si f es creciente sobre I o decreciente sobre I.
- f puede ser estrictamente monótona : se dice que f es estrictamente monótona si f es estrictamente creciente o estrictamente decreciente sobre I.
Cuando una función es creciente o estrictamente creciente, las imágenes f(x) están ubicadas en el mismo orden que los antecedentes. Se dice entonces que f conserva el orden.
En la práctica, el estudio de la variación de una función f se realiza mediante una tabla de variaciones (en dos líneas) que ayuda a resumir las variaciones de la siguiente manera :
- La primera línea de la tabla de variación marca los intervalos del conjunto de definiciones de la función. Allí figuran los valores del conjunto inicial (abscisas) sobre los cuales el sentido de la variación de la función cambia.
- En la segunda línea de la tabla, aparecen flechas que representan el sentido de variación de la función.

Los valores máximos M y mínimos m de una función f sobre el intervalo I corresponden respectivamente al valor más grande y más pequeño de f(x) con x que varía sobre I. En el ejemplo anterior, f alcanza su máximo en las coordenadas (-2, 3) (3 siendo el máximo de la función) y su mínimos en el punto (5, -3). Los valores máximos y mínimos se llaman los extremos de la función.
6. Las funciones en Data Science
En análisis de datos, las funciones son utilizadas en todos los niveles. Por ejemplo en Python, las bibliotecas utilizadas para aplicar transformaciones sobre los datos son paquetes de funciones. Según lo que se desee hacer (por ejemplo manipular un texto o imágenes), se utilizará un paquete de funciones dedicadas a la manipulación de un tipo de datos.
En Python, existen funciones para todo, desde la lectura hasta el registro, pasando por la transformación de datos o de archivos).
Si quieres saber más sobre cómo utilizar funciones en Python, ¡descubre nuestras formaciones!