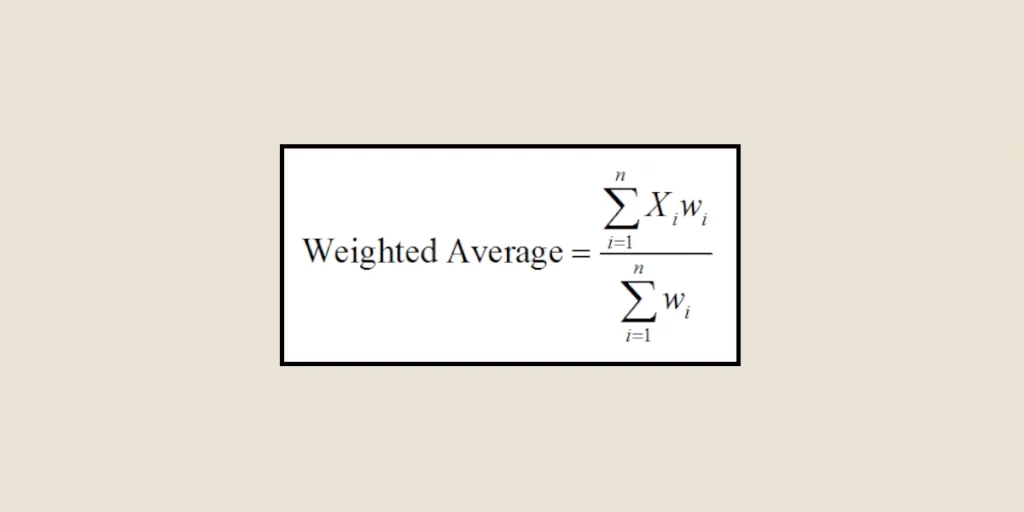El cálculo de un simple promedio, si se emplea con fines de análisis, puede resultar engañoso. Al aplicar una ponderación a algunos de los números de una lista, es posible obtener una percepción mucho más precisa.
No toda la información tiene la misma importancia, y un análisis acertado de cualquier sector debe tener en cuenta este factor. Si solo utilizamos fórmulas simples como el promedio de una serie de números, a menudo tomaremos decisiones inadecuadas.
Tomemos un ejemplo simple para ilustrar esta idea. Un profesor decide al final del año si los estudiantes son aptos para pasar al siguiente grado, con base en lo siguiente: el promedio de sus notas debe ser superior a 10. Aquí hay un cuadro simplificado con las notas de varios estudiantes.
| Joey | Monica | Rachel | |
|---|---|---|---|
| control 1 | 12 | 7 | 11 |
| examen trimestre | 9 | 12 | 12 |
| control 2 | 14 | 6 | 10 |
| examen de fin de año | 8 | 14 | 11 |
| Promedio | 10,75 | 9,75 | 11 |
Aquí tenemos tres estudiantes: Joey, Monica y Rachel. Cada uno ha sido sometido a 4 pruebas de evaluación de conocimientos: control 1, examen trimestre, control 2, etc.
Si aplicamos un promedio a estas notas, resulta que dos estudiantes tienen una nota suficiente para pasar al siguiente grado: Joey y Rachel. Monica, por su parte, queda reprobada.
El principio de la media ponderada
En el cálculo del promedio ponderado, tomamos en cuenta un factor: no todas las pruebas tienen la misma importancia. Así, el examen de trimestre tiene 2 veces más importancia que los controles. Y el examen de fin de año tiene 4 veces más que un simple control porque cubre todos los temas abordados durante el año.
El promedio ponderado toma en cuenta este factor aplicando una ponderación (un peso) a cada una de las pruebas. Así, los controles tienen un coeficiente 1, el examen de trimestre un coeficiente 2, el de fin de año un coeficiente 4.
A partir de ahí, el promedio ponderado se calcula así:
(nota x coeficiente) + (nota x coeficiente) + (…) / suma de los coeficientes
| coefficient | Joey | Monica | Rachel | |
|---|---|---|---|---|
| control 1 | 1 | 12 | 7 | 11 |
| examen trimestre | 2 | 18 | 24 | 24 |
| control 2 | 1 | 14 | 6 | 10 |
| examen de fin de año | 4 | 32 | 56 | 44 |
| Promedio ponderado | 9,5 | 11,63 | 11,13 |
Por ejemplo, el promedio ponderado de Joey se calcula así: (12 x 1) + (9 x 2) + (14 x 1) + (8 x 4) / 8. ¿Y qué vemos al aplicar este cálculo? Una situación completamente diferente. Ahora, Monica aparece como la mejor estudiante y pasa con creces. Mientras que Joey, por su parte, queda reprobado.
Ventajas del promedio ponderado
Como puedes ver en el ejemplo anterior, el promedio ponderado revela una situación mucho más justa del nivel de cada estudiante. Así que tenemos aquí una herramienta que abre el camino a decisiones acertadas.
Tomemos ahora el caso de una tienda online que recoge opiniones de sus clientes. Ha implementado un sistema de alerta: si el promedio de las calificaciones en una semana es inferior a 3 sobre 5, deben tomarse medidas correctivas de inmediato. Sí, pero… Imaginemos que entre el lote, la tienda tiene 5 clientes específicos que por sí solos representan el 60% del volumen de negocios. En la medida en que su opinión es crucial, será bueno atribuir a sus calificaciones un peso mucho más importante que el de compradores ocasionales. Así, el promedio ponderado podrá destacar un fenómeno que podría pasar desapercibido.
Ponderación de una cartera de acciones

Este principio del promedio ponderado es tan importante que interviene en el cálculo de las ganancias de capital que un inversor debe declarar al fisco tras la venta de acciones. Una vez más, un ejemplo ilustrará el porqué de la cuestión.
Supongamos que un inversor adquiere:
- 100 acciones a 20 € de una startup el primer año
- 200 acciones a 50 € de la misma startup al año siguiente.
Si el inversor simplemente opera con un promedio “clásico” tomando en cuenta lo que ha gastado, obtiene un promedio de 35 €. Sin embargo, esta cifra es engañosa, ya que da la misma importancia a los montos pagados (20 y 50 €). Si revendiera sus acciones al precio de 38 €, el inversor podría tener la impresión de haber realizado una ganancia de capital. En realidad, no es así.
Para obtener el promedio ponderado, multiplicamos las 100 acciones por 20 € para el primer año y las 200 acciones por 50 € para el segundo año, es decir, 2 000 + 10 000 y entonces 12 000 euros en total. Este monto global se divide luego por el número de acciones adquiridas durante este periodo (300). Obtenemos entonces un promedio ponderado de 40 €. Resulta que una reventa a 38 € correspondería a una pérdida de capital.
Una ayuda en la toma de decisiones
El promedio ponderado ayuda a decidir realmente si es prudente intervenir en una situación dada. Por lo tanto, es una herramienta de análisis a la que no se debe dar la espalda.