Si alguna vez has estado interesado en los métodos de reducción de dimensiones, probablemente ya hayas estudiado el Análisis de Componentes Principales o ACP. En este artículo, abordaremos otro de los métodos de reducción de dimensiones que existen: t-SNE o t-distributed Stochastic Neighbor Embedding en inglés. Este algoritmo propone un método diferente del ACP.
T-SNE es una técnica de reducción de dimensiones utilizada para la explotación de datos de grandes dimensiones que ha sido desarrollada en 2008 por Geoffrey Hinton y Laurens Van Der Maaten. Como en el caso del ACP, el objetivo es determinar un espacio más de menor dimensión conservando siempre la misma distancia entre los puntos.
t-SNE y ACP
El análisis de componentes principales es un método ampliamente utilizado en la reducción de dimensiones que busca representar datos en un hiperplano cercano para mantener la varianza de la nube de datos tanto como sea posible. Es decir, se trata de representar los datos en un subespacio de menor dimensión maximizando la inercia total de la nube proyectada en este espacio. Si quieres saber más sobre el ACP, mira este video que hicimos sobre este tema:
El principio del t-SNE
El algoritmo t-SNE consiste en crear una distribución de probabilidad que represente las similitudes entre vecinos en un espacio de gran dimensión y en un espacio de menor dimensión. Por similitud, intentaremos convertir las distancias en probabilidades. Se divide en 3 pasos :
- 1° paso : Calculamos las similitudes de puntos en el espacio inicial de grandes dimensiones. Para cada punto xi centramos una distribución gaussiana alrededor de este punto. Luego medimos, para cada punto xj (i diferente de j), la densidad bajo esta distribución gaussiana definida previamente. Finalmente, normalizamos para cada uno de los puntos. De este modo obtenemos una lista de probabilidades condicionales observadas:

La desviación estándar se define por un valor llamado perplejidad que corresponde al número de vecinos alrededor de cada punto. Este valor lo establece el usuario de antemano y permite estimar la desviación estándar de las distribuciones gaussianas definidas para cada punto xi. Cuanto mayor es la perplejidad, mayor es la variación.
- 2° paso : Necesitamos crear un espacio dimensional más pequeño en el que representaremos nuestros datos. Obviamente, al principio no conocemos las coordenadas ideales en este espacio. Por tanto, vamos a distribuir los puntos de forma aleatoria en este nuevo espacio. El resto es bastante similar al paso 1, calculamos las similitudes de los puntos en el espacio recién creado, pero usando una distribución t-Student y no una gaussiana. De la misma forma obtenemos una lista de probabilidades :
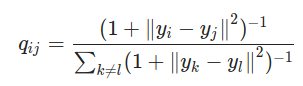
- 3° paso : para representar fielmente los puntos en el espacio dimensional más pequeño, lo ideal sería que las medidas de similitud en los dos espacios coincidieran. Entonces, necesitamos comparar las similitudes de los puntos en los dos espacios usando la medida Kullback_Leibler (KL). Luego tratamos de minimizarlo mediante la gradiente descendente para obtener el mejor yi posible en un espacio de dimensiones pequeñas. Esto equivale a minimizar la diferencia entre las distribuciones de probabilidad entre el espacio original y el espacio de menor dimensión.
Comparación de métodos ACP y t-SNE
Para comprender mejor las diferencias entre los dos métodos PCA y t-SNE, consideremos el conjunto de datos MNIST. Para cada uno de los dos métodos, hemos representado los datos en un espacio bidimensional.
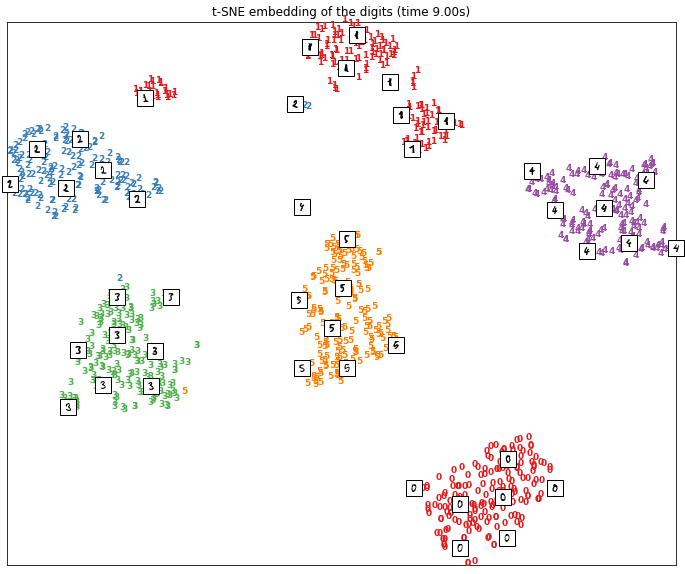
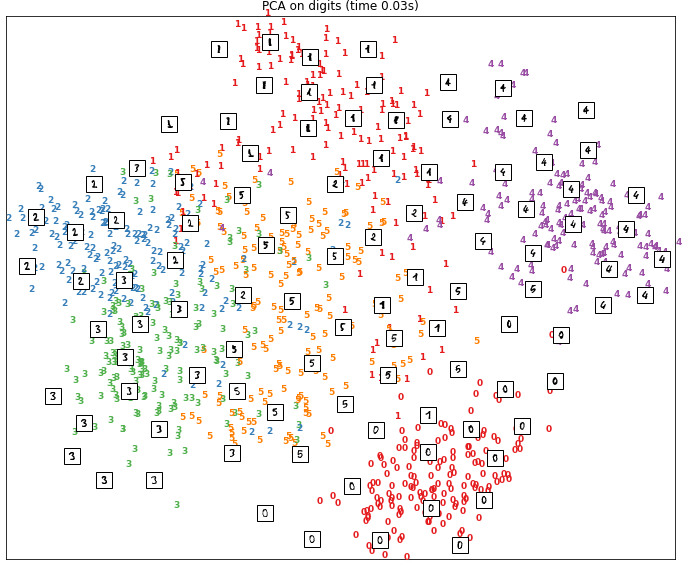
En la primera figura tenemos el resultado obtenido por reducción de dimensión con el método t-SNE. En el segundo, tenemos el resultado obtenido con un análisis de componentes principales.
Como podemos ver, t-SNE ha logrado agrupar los datos cercanos y separar los datos diferentes. Los puntos se representan en grupos, cada uno de los cuales corresponde a un número entre 1 y 6.
En el caso de los resultados obtenidos con PCA, la separación de datos en el espacio en 2 dimensiones es mucho menos clara. Podemos ver que para algunos dígitos como 0 los puntos correspondientes están bien agrupados. Sin embargo, para otros dígitos como los puntos asociados con el número 5, se distribuyen de manera más difusa.
Si quieres formarte en temas como las técnicas de reducción de dimensiones, ¡ven a descubrir nuestras formaciones en formato bootcamp o en continuo!