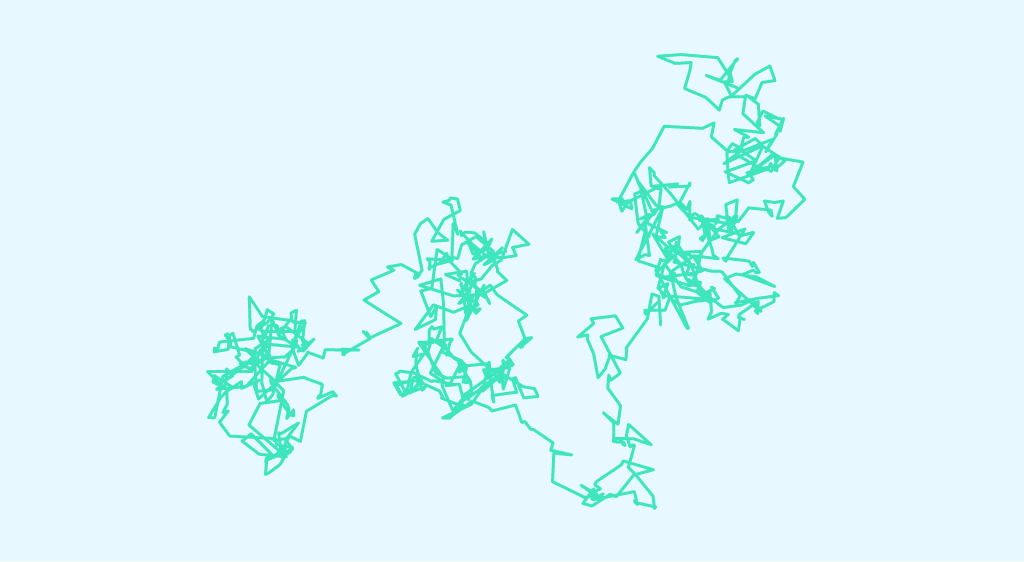
Tomemos una partícula de tamaño micrométrico sumergida en líquido. Esa partícula va a tener un movimiento aleatorio debido a los choques con otras pequeñas partículas en esta “gran” partícula. Es el principio del movimiento browniano, también llamado proceso de Wiener.
Históricamente, fue en 1827 cuando el botanista Robert Brown descubrió el movimiento browniano. Observó el movimiento caótico de granos de polen en el agua.
Hay que esperar a 1905 para que Albert Einstein describa de manera cuantitativa el movimiento browniano. En particular, vincula la media cuadrática de la distancia recorrida a la duración de la observación. Sus cálculos serán validados experimentalmente por Jean Perrin. Los experimentos de este último también permitirán determinar la constante de Avogadro.
El movimiento browniano posee aplicaciones en diferentes ámbitos. En el campo de la física, se utiliza sobre todo para determinar el movimiento de pequeñas partículas como por ejemplo los aerosoles por el aire. Se toma en cuenta una fuerza aleatoria (sobre todo en las ecuaciones de Langevin).
El movimiento browniano también posee aplicaciones matemáticas con procesos estocásticos. Desde 1857, el trabajo de Robert Brown empieza a suscitar un gran interés y varios científicos definen las propiedades del movimiento browniano. cos: modelos probabilísticos que permiten estudiar un fenómeno aleatorio a lo largo del tiempo. Se usa mucho en probabilidad, y ya existen varias aplicaciones en el campo de las finanzas.
La aplicación del movimiento browniano en las micromanipulaciones de moléculas de ADN
1- El principio
A título de ejemplo, vamos a interesarnos por una de las aplicaciones físicas del movimiento browniano que es la micromanipulación de la molécula de ADN. Es posible micromanipular moléculas de ADN gracias a varias herramientas como pinzas ópticas o pinzas magnéticas.
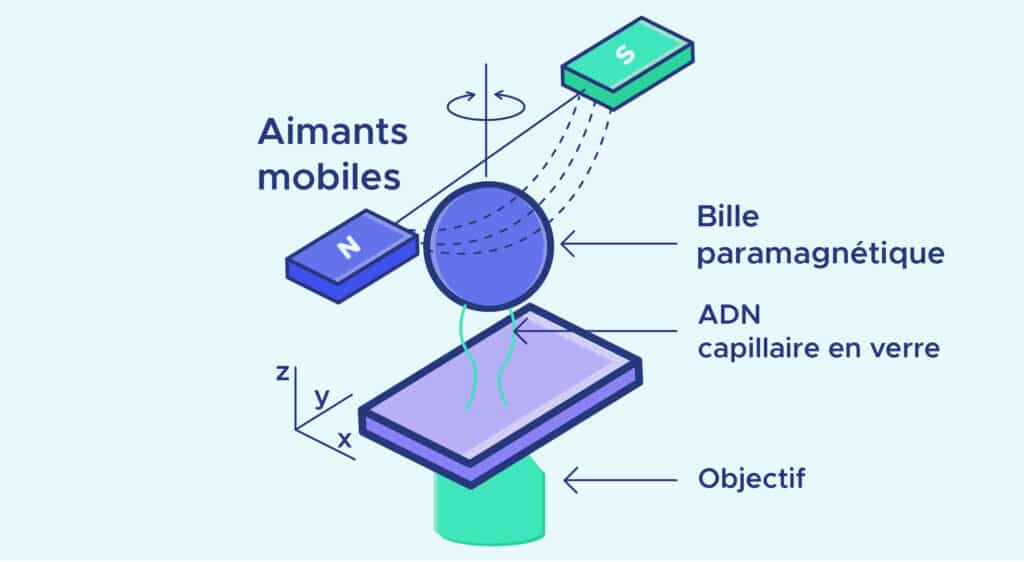
El principio de micromanipulación es el siguiente :
- Se fija un extremo de la molécula de ADN a un capilar de cristal
- En el otro extremo, se coloca una bola magnética. Esa bola se colocará en el campo de un imán.
- El desplazamiento de los imanes va a permitir tirar de la molécula de ADN o hacerla girar sobre sí misma para crear espirales.
2- El interés del movimiento browniano
Una vez presentado el contexto, podemos preguntarnos dónde interviene el movimiento browniano.
La fuerza necesaria para estirar la molécula de ADN da información bastante importante sobre nuestra macromolécula.
Esa fuerza es muy floja (del orden del piconewton, es decir 10-12 newton). Al ser floja, no se puede medir con facilidad con aparatos de medición clásicos que están limitados por la agitación térmica.
Sin embargo, el movimiento browniano va a permitir medir la fuerza. Efectivamente, la agitación térmica va a generar una fuerza aleatoria que apartará la bola de su posición de equilibrio. Los cálculos permiten demostrar que la fuerza de estiramiento de la molécula de ADN está directamente vinculada con las fluctuaciones cuadráticas medias.
Ahora, solo nos queda determinar las fluctuaciones cuadráticas medias. Para ello, tenemos que inspirarnos en el experimento de Jean Perrin.
- Una primera etapa consiste en registrar los movimientos de la partícula esférica colocada en el extremo de la molécula de ADN con ayuda de una cámara conectada a un microscopio.
- En segundo lugar, los softwares de reconocimiento de vídeo permiten acceder a los datos de la bola en cada instante. Y las coordenadas permiten calcular las fluctuaciones brownianas.
3- El uso de Python para acceder a los datos de la bola
A partir del vídeo, se puede acceder a los datos de la bola de manera mucho más compleja gracias a Python.
Efectivamente, una vez que el vídeo se convierte en sucesión de imágenes, se utiliza la biblioteca imageio de Python. Permite trabajar con las imágenes presentándolas como cuadros de 3 dimensiones. Las dos primeras dimensiones permiten determinar la posición de un píxel y la tercera dimensión nos da información sobre la intensidad del color (lo que nos dará el color del píxel). Una vez que las imágenes se convierten en matices de gris, nos podemos acercar a un cuadro en dos dimensiones, puesto que los valores de la tercera dimensión serán todos iguales (ya que la imagen es en tonalidades de gris). Basta entonces con crear funciones que permitan, mediante un método baricéntrico, determinar las coordenadas del píxel de máxima intensidad. Repitiendo ese proceso en la sucesión de imágenes, obtenemos al final nuestras coordenadas de la bola en cada instante.
El acceso a las coordenadas permite acceder a las fluctuaciones brownianas, y a la fuerza de estiramiento de la molécula de ADN.
De este modo, el movimiento browniano es muy útil en la micromanipulación de la molécula de ADN. El trabajo sobre el análisis del vídeo también es un elemento muy importante. Como ya hemos visto, este proceso puede hacerse con la ayuda de Python.
Los cursos propuestos por DataScientest permiten aprender a dominar Python, una herramienta indispensable en Data Science. Proponemos también un módulo sobre el tratamiento de imágenes: Introducción a la Computer Visión con OpenCV
Sobre el autor