Como su nombre indica, los algoritmos de optimización tienen como objetivo encontrar una buena solución (idealmente la mejor) a un problema, en función de ciertos criterios u objetivos específicos.
Entre los muchos algoritmos de optimización disponibles, algunos de ellos se inspiran en lo que ya existe en la naturaleza: son los algoritmos biomiméticos. Pueden inspirarse en la inteligencia colectiva de los insectos (optimización por enjambre) o en los mecanismos de la selección natural, como en los algoritmos de optimización genética (también llamados evolucionistas).
Los mecanismos de la selección natural (derivados notablemente de la teoría de Darwin) tienen como objetivo seleccionar a los individuos mejor adaptados para permitir que la especie mejore a lo largo de las generaciones.
En el caso de los algoritmos genéticos, los datos de nuestro problema se almacenan en forma de un vector que representa el genoma de los diferentes individuos. Se trata de constituir una población inicial de individuos y luego seleccionar los mejores, generación tras generación. Esta selección se realiza según criterios de puntuación, los individuos mejor puntuados son seleccionados para la próxima generación.
Para ilustrar este artículo, tomaré el ejemplo de un turista que desea pasar 10 días en el parque natural regional del Morvan en Borgoña. Quiere visitar las ciudades que ofrecen más puntos de interés históricos recorriendo la menor cantidad de kilómetros. En los días tres y ocho, quiere pasar la noche en un hotel de al menos 3 estrellas.
Existen, por supuesto, librerías llave en mano más sofisticadas para utilizar estos algoritmos, pero el ejemplo de código desarrollado aquí permitirá comprender los mecanismos básicos.
Los datos
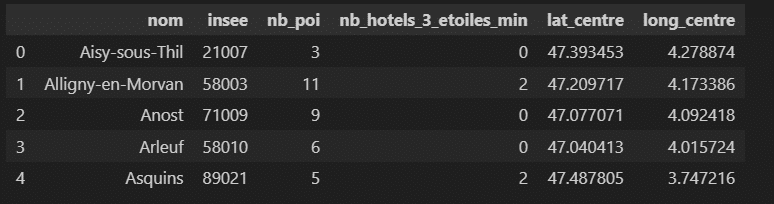
Para alimentar mis datos, recuperé en OpenStreetMap los puntos de interés (POI) históricos de cada municipio del parque. Los datos gubernamentales franceses me permitieron conocer la ubicación de los hoteles de 3 estrellas o más, así como las coordenadas geográficas del centro de la ciudad con vistas a los cálculos de distancia.
Constitución de la población inicial
Si quisiéramos encontrar directamente la solución óptima al problema, deberíamos considerar todas las combinaciones posibles y evaluar cómo responden al problema. Desafortunadamente, las capacidades de cálculo actuales no lo permiten para problemas algo complejos. Es por eso que hay que constituir una población cuyo volumen sea lo suficientemente grande como para constituir una muestra representativa, pero no demasiado grande para no alargar excesivamente los tiempos de cálculo. Un compromiso posible puede ser compensar una población más pequeña aumentando el número de iteraciones (o generaciones). Esta etapa implica cierta dosis de empirismo y se pueden intentar varias pruebas hasta llegar a un buen compromiso. He elegido una población inicial de 1500 individuos.
En cuanto a las características genéticas de cada individuo, la solución es extremadamente simple: el genoma se constituye de manera aleatoria a partir de los diferentes valores.
En nuestro caso, utilizamos una función de generación de listas aleatorias a partir de los códigos INSEE de los diferentes municipios del parque del Morvan.
Evaluación de los individuos
Una vez constituida la primera generación de la población, cada individuo debe ser evaluado para que los mejores puedan ser seleccionados.
Aquí, no hay una solución general, cada problemática requiere su propio método de evaluación para la selección de los mejores individuos. Una vez realizada la evaluación, el proceso de selección y constitución de las nuevas generaciones podrá llevarse a cabo.
En mi caso, los dos criterios de puntuación son la distancia total recorrida y el número total de puntos de interés del recorrido. Para evitar tener recorridos con pocos kilómetros, pero sin muchos puntos de interés (o viceversa), he decidido agrupar por deciles los recorridos más eficientes tanto en términos de kilometraje como de puntos de interés. Así, los recorridos puntuados con 2 pertenecen a ambos segundos deciles de estas dos categorías. Los recorridos puntuados con 10 agrupan, además de sus deciles, todos los recorridos que no cumplen con este requisito de doble pertenencia a los deciles anteriores.
Como el criterio relacionado con los alojamientos en hoteles necesariamente iba a cambiar en función de las iteraciones, decidí no retenerlo como criterio puro de puntuación pero lo utilizo como filtro en mis dataframes.
Selección y constitución de la próxima generación
En este punto, se pueden seguir dos estrategias. Elitismo o fusión. En ambos casos, el objetivo es obtener una nueva generación cuyo número de individuos sea igual a la generación anterior.
En el caso de el elitismo, la evaluación se lleva a cabo primero, y luego los genomas de los individuos mejor puntuados se retoman directamente para la próxima generación. El resto de la población se completará con individuos resultantes de cruces (como ocurre con la reproducción sexual) o de mutaciones.
En el caso de la fusión, la nueva generación (con el mismo número de individuos que la anterior) se crea primero mediante cruces y mutaciones. La selección se lleva a cabo posteriormente y solo los individuos mejor evaluados son retenidos en el número de efectivos de la generación anterior.
En el marco de mi proyecto, he optado por el sistema elitista siguiendo el viejo adagio según el cual no se cambia un equipo que gana. Más seriamente, cada sistema presenta sus propias ventajas e inconvenientes. Si la fusión permite aumentar la diversidad genética de los individuos, el elitismo permite preservar a los individuos mejor adaptados. Es esta cualidad la que me decidió a elegir el elitismo. Para la cohorte, he seleccionado al 20% de los mejores individuos de la población como élite para la selección de la próxima generación. Se acepta en general que la proporción de élites puede estar entre el 5% y el 20%, yo he elegido el extremo alto de ese rango.

Cruce y mutación
Estos dos procesos naturales permiten la creación de nuevos individuos cuyas características propias de su genoma les permitirán potencialmente estar mejor adaptados a su entorno. Al estar mejor adaptados, estos individuos tendrán más posibilidades de sobrevivir y, por lo tanto, de reproducirse y transmitir sus genes.
En el caso de los algoritmos genéticos, la lógica es similar. Los individuos mejor evaluados son seleccionados para la generación siguiente y posteriormente tendrán más probabilidades de transmitir sus características.
El cruce consiste en retomar los mecanismos de la reproducción sexual. Los genes de los dos ascendientes se mezclan para constituir un nuevo genoma único.

En algunos modelos, se propone mezclar los genomas parte por parte (mitad o en pares de genes). En mi caso, he privilegiado un enfoque similar al existente en la naturaleza, gen por gen.
En mi caso, la función de cruce de los individuos viene acompañada de una pequeña dosis de mutaciones. En teoría, en un lugar dado, la selección se realiza únicamente entre el gen de cada padre. Con este sistema, una misma ciudad podría aparecer dos veces en el mismo recorrido, lo cual no es deseable. Por lo tanto, he implementado una restricción para evitar este fenómeno.
En la naturaleza, también existen procesos de mutación. El genoma de un individuo se modificará independientemente de todo proceso de reproducción. Este mecanismo permite aumentar la variabilidad genética provocando soluciones genéticas inéditas.
3 posibilidades de mutaciones pueden ocurrir.
Inserción: un gen se desplaza para insertarse después de otro

Pérmutación (o intercambio): dos genes permutan su lugar
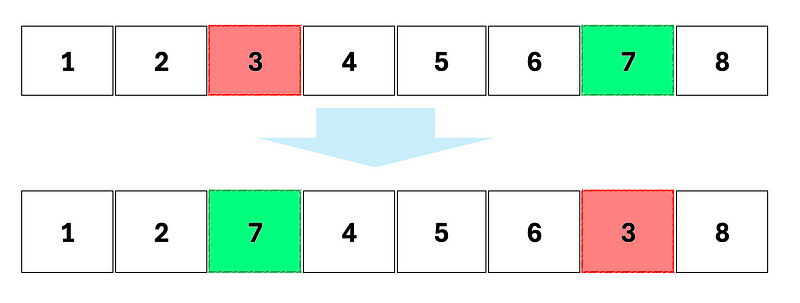
Inversión de secuencia: el orden de una parte del genoma se invierte

El porcentaje de mutaciones suele representar el 5% de los nuevos individuos, pero he podido observar tasas de mutaciones de hasta el 10%. Dado que el sistema elitista tiende a reducir la variabilidad de los genomas, he elegido este valor del 10% como compensación.
Iteración del proceso y solución
Al iterar el proceso de selección y constitución de las nuevas generaciones, se obtendrá progresivamente individuos cuyas características permitirán responder cada vez mejor al problema dado.
La pregunta que se plantea ahora es cuándo detener el proceso. Esto depende de nuestras restricciones.
Si tenemos un tiempo limitado, podemos detener las iteraciones después de un cierto tiempo de ejecución. También se puede intentar alcanzar un umbral correspondiente a un criterio (un número de kilómetros ideal para nuestro trayecto, por ejemplo, o que cada ciudad visitada tenga un número mínimo de puntos de interés). En modo experimental, se pueden lanzar iteraciones repetidamente y analizar el momento en que las iteraciones ya no aportan una mejora significativa. Luego, se fija un número límite de iteraciones.
En el marco de este ejercicio, para no tener tiempos de cálculo excesivamente largos, me he conformado con 200 iteraciones.
En conclusión
Como en muchos ámbitos, la naturaleza una vez más es una gran fuente de inspiración. Este ejemplo simple permite comprender cómo se pueden optimizar problemas complejos inspirándose en soluciones naturales adoptadas desde hace cientos de millones de años.
Después de 200 iteraciones, obtuve el siguiente recorrido:
Glux-en-Glenne, Roussillon-en-Morvan, Alligny-en-Morvan, Anost, Quarré-les-Tombes, Saint-Léger-Vauban, Avallon, Vézelay, Bazoches, Pierre-Perthuis… para un total de 154 km y un total de 115 puntos de interés en el recorrido.
Al aumentar el número de iteraciones podría haber mejorado aún más la solución, pero el objetivo de este script es más explicativo que de rendimiento. No quise alargar demasiado los tiempos de cálculo para la ejecución.
Para tu información, el uso de dataframes Pandas no es óptimo en términos de rendimiento, pero nuevamente, el objetivo principal de este script es ser explicativo.
Puedes encontrar mi código completo en mi repositorio de git.