La curva ROC (Receiver Operating Characteristic) y su métrica asociada AUC (Area Under the Curve) son herramientas fundamentales para la evaluación de modelos de clasificación en machine learning. Estas métricas proporcionan información crucial sobre la capacidad de un modelo para distinguir las clases, particularmente en escenarios de clasificación binaria.
¿Cuáles son los fundamentos de la ROC AUC?
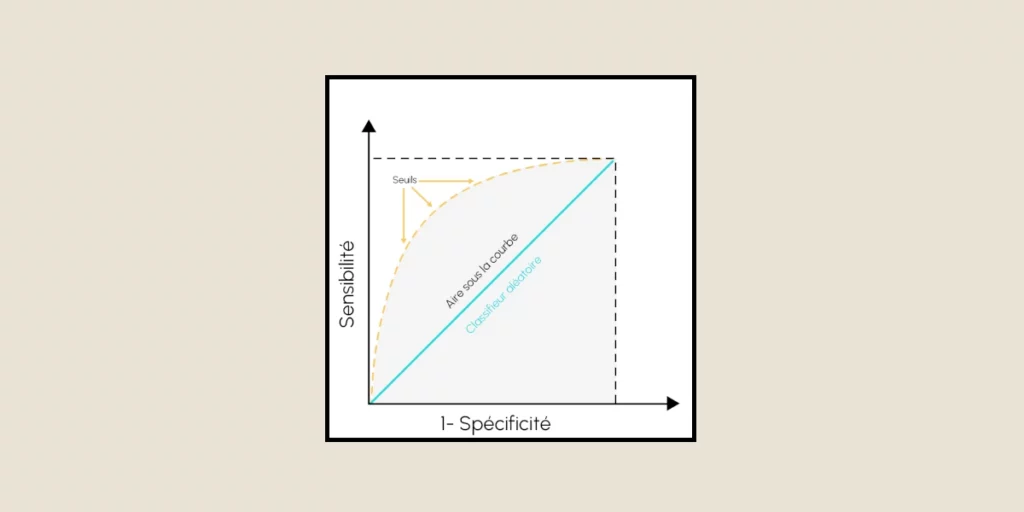
La curva ROC es, en su esencia, una representación gráfica que ilustra el rendimiento de un modelo de clasificación a través de diferentes umbrales de decisión. Esta curva traza la relación entre dos métricas de rendimiento críticas: la sensibilidad (también conocida como la tasa de verdaderos positivos) y la especificidad complementaria a la tasa de falsos positivos. Cuando el umbral de decisión del modelo cambia, estas tasas evolucionan, creando una curva que revela la capacidad discriminativa del modelo.
El área bajo esta curva, conocida como AUC, proporciona un valor escalar único que cuantifica el rendimiento global del clasificador. Un clasificador perfecto alcanza un AUC de 1.0, mientras que una predicción aleatoria da un AUC de 0.5, representada por una línea diagonal en el gráfico ROC.
¿Cómo comprender el rendimiento del modelo a través de la ROC AUC?
Al evaluar un modelo de clasificación, la curva ROC proporciona información valiosa sobre sus características de rendimiento. La curva comienza en la esquina inferior izquierda (0,0) y se extiende hasta la esquina superior derecha (1,1). El camino que recorre entre estos puntos nos informa sobre la capacidad del modelo para identificar correctamente los casos positivos y negativos.

Una ventaja mayor de la ROC AUC es su insensibilidad al desequilibrio de clases. Esto la hace particularmente valiosa para aplicaciones reales donde una clase puede estar significativamente más presente que la otra. Por ejemplo, en el diagnóstico médico, donde el número de pacientes sanos generalmente supera con creces al de pacientes enfermos, la ROC AUC proporciona una evaluación equilibrada del rendimiento del modelo.
¿Cuáles son las aplicaciones prácticas e interpretación?
En las aplicaciones de machine learning, la ROC AUC cumple varias funciones importantes. Ayuda en la selección de modelos, el ajuste de parámetros y la comparación de diferentes algoritmos de clasificación. Esta métrica es especialmente útil cuando el umbral de decisión óptimo no se conoce de antemano o podría requerir ajustes según exigencias específicas.
Tomemos el ejemplo de una prueba diagnóstica médica: una AUC alta indica que la prueba puede distinguir efectivamente entre los estados sano y enfermo. La curva ROC permite a los profesionales de la salud elegir un umbral que optimice la sensibilidad (identificación correcta de pacientes enfermos) y la especificidad (identificación correcta de pacientes sanos) en función de los costos relativos de los falsos positivos y los falsos negativos.
¿Cuáles son los conceptos avanzados y consideraciones?
Aunque la ROC AUC está principalmente asociada a la clasificación binaria, puede extenderse a problemas multiclase a través de varios enfoques. Un método común es el enfoque «uno-contra-todo», donde se generan curvas ROC separadas para cada clase contra todas las demás.
La matriz de confusión juega un papel crucial en la comprensión de la ROC AUC. Proporciona los conteos fundamentales de verdaderos positivos, verdaderos negativos, falsos positivos y falsos negativos que forman la base del cálculo de las tasas trazadas en la curva ROC.
¿Cómo es la implementación y qué herramientas se utilizan?

Los frameworks modernos de machine learning proporcionan herramientas robustas para calcular y visualizar la ROC AUC. Bibliotecas como scikit-learn ofrecen implementaciones directas a través de funciones como roc_auc_score, facilitando la integración de esta métrica en los pipelines de evaluación de modelos.
¿Cuáles son las mejores prácticas y limitaciones?
Aunque la ROC AUC es una métrica poderosa, es importante comprender sus limitaciones. No toma en cuenta las diferencias de costo entre falsos positivos y falsos negativos, lo cual limita su aplicabilidad en algunos contextos. Además, en conjuntos de datos muy desequilibrados, métricas complementarias como las curvas precisión-recall pueden ofrecer una mejor evaluación del rendimiento.
¿Cómo implementar de manera práctica?
La comprensión técnica de la implementación de los cálculos de la ROC AUC es crucial para los profesionales en machine learning. El proceso comienza por las probabilidades predichas por el modelo para cada clase. Estas probabilidades se ordenan para crear diferentes valores de umbral, y para cada umbral, se calculan la tasa de verdaderos positivos y la tasa de falsos positivos.
¿Qué técnicas de optimización del rendimiento existen?
Para maximizar la eficiencia de la ROC AUC en la evaluación de modelos, se pueden emplear varias técnicas de optimización. La ingeniería de características desempeña un papel crucial en la mejora del rendimiento del modelo. Además, el tratamiento adecuado de los valores faltantes y los valores atípicos puede impactar significativamente la forma de la curva ROC y la AUC resultante.

¿Cuáles son las aplicaciones sectoriales específicas?
Diferentes sectores tienen requisitos y consideraciones únicas al aplicar el análisis ROC AUC. En los servicios financieros, las curvas ROC ayudan a evaluar los modelos de puntuación de crédito. El sector de la salud utiliza intensivamente la ROC AUC en las pruebas diagnósticas. En aplicaciones de ciberseguridad, la ROC AUC ayuda a evaluar los sistemas de detección de anomalías.
¿Cuál es la conclusión?
La ROC AUC permanece como una de las métricas más importantes para la evaluación de modelos de machine learning. Su capacidad para proporcionar una evaluación independiente del umbral del rendimiento del clasificador, combinada con su insensibilidad al desequilibrio de clases, la convierte en una herramienta inestimable en el arsenal del profesional en machine learning. Comprenderla e interpretarla correctamente es esencial para desarrollar modelos de clasificación efectivos y tomar decisiones informadas respecto a su despliegue en aplicaciones reales.