El clustering es una disciplina particular del Machine Learning que tiene como objetivo separar sus datos en grupos homogéneos con características comunes. Es un campo muy popular en el marketing, por ejemplo, donde a menudo se intenta segmentar las bases de clientes para detectar comportamientos particulares.
En artículos anteriores, presentamos dos algoritmos de agrupación: el algoritmo de K-medias/K-means y el algoritmo CAH-clasificación jerárquica ascendente.
Nos parecía fundamental continuar este proceso de aprendizaje con el DBSCAN.
¿Cómo funciona el algoritmo DBSCAN ?
El DBSCAN es un algoritmo no supervisado muy conocido en materia de Clustering. Fue presentado en 1996 por Martin Ester, Hans-Peter Kriegel, Jörg Sander y Xiawei Xu.
En este artículo detallaremos cómo funciona y cómo implementarlo en Python utilizando librerías como Scikit-Learn. Sus campos de aplicación son diversos: análisis cartográfico, análisis de datos, segmentación de una imagen, etc.
El principio
A partir de unos puntos y un número entero k, el algoritmo pretende dividir los puntos en k grupos, llamados clústeres, homogéneos y compactos. Veamos el siguiente ejemplo:
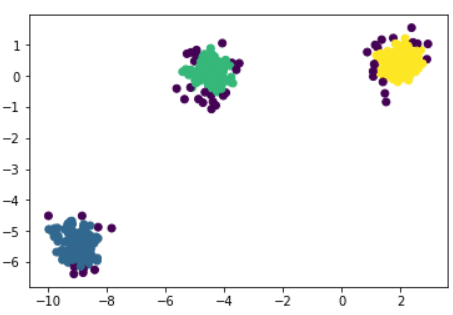
El DBSCAN es un algoritmo sencillo que define los clústeres mediante la estimación de la densidad local. Se puede dividir en 4 etapas:
- Para cada observación miramos el número de puntos a una distancia máxima ε de ella. Esta zona se denomina ε-vecindad de la observación.
- Si una observación tiene al menos un cierto número de vecinos, incluida ella misma, se considera una observación central. En este caso, se ha detectado una observación de alta densidad.
- Todas las observaciones en la vecindad de una observación central pertenecen al mismo clúster. Puede haber observaciones centrales cercanas entre sí. Por lo tanto, de un paso a otro, se obtiene una larga secuencia de observaciones centrales que constituyen un único clúster.
- Cualquier observación que no sea una observación central y que no tenga ninguna observación central en su vecindad se considera una anomalía.
Por tanto, es necesario definir dos datos antes de utilizar DBSCAN:
¿Qué distancia ε hay que determinar para cada observación la ε-vecindad? ¿Cuál es el número mínimo de vecinos necesario para considerar una observación como una observación central?
Estos dos datos son facilitados libremente por el usuario. A diferencia del algoritmo k-means o de la clasificación jerárquica ascendente, no es necesario definir de antemano el número de clústeres, lo que hace que el algoritmo sea menos rígido.
Otra ventaja de DBSCAN es que también permite gestionar los valores atípicos o las anomalías. En la figura anterior se observa que el algoritmo ha determinado 3 clústeres principales: azul, verde y amarillo. Los puntos de color morado son anomalías detectadas por el DBSCAN. Obviamente, dependiendo del valor de ε y del número de vecinos mínimos, la partición puede variar.
Noción de distancia y elección de ε
En este algoritmo hay dos puntos clave:
¿Cuál es la métrica utilizada para evaluar la distancia entre una observación y sus vecinos? ¿Cuál es la ε ideal?
En DBSCAN por lo general se utiliza la distancia euclidiana, siendo p = (p1,….,pn) y q = (q1,….,qn):
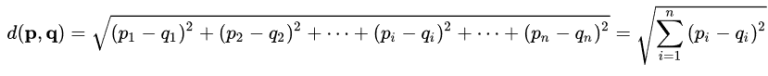
En cada observación, para contar el número de vecinos a como máximo una distancia ε, calculamos la distancia euclidiana entre el vecino y la observación y comprobamos si es inferior a ε.
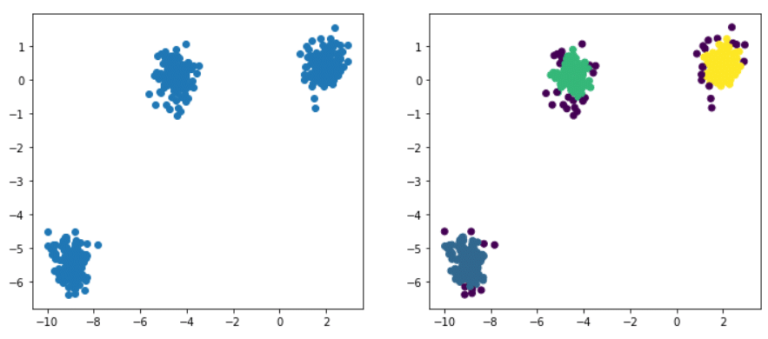
Ahora queda saber cómo elegir la épsilon correcta. Supongamos que en nuestro ejemplo elegimos probar el algoritmo con diferentes valores de ε. Aquí está el resultado:
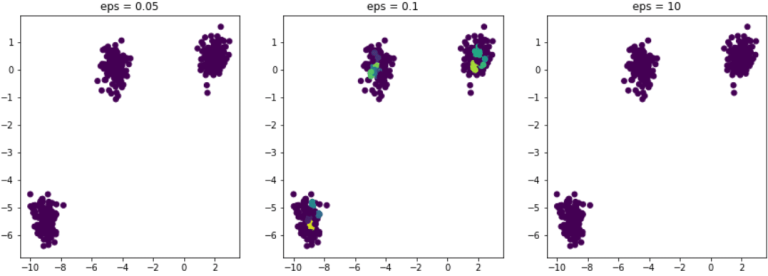
En los tres ejemplos, el número mínimo de vecinos está fijado siempre en 5.
Si ε es demasiado pequeña, la ε-vecindad es demasiado pequeña y todas las observaciones del conjunto de datos se consideran anomalías.
Es el caso de la figura de la izquierda eps = 0,05.
Por otro lado, si épsilon es demasiado grande, cada observación contiene en su ε-vecindad todas las demás observaciones del conjunto de datos. En consecuencia, obtenemos un único clúster. Por tanto, es muy importante calibrar adecuadamente la ε para obtener una partición de calidad.
Un método sencillo para optimizar la ε consiste en buscar para cada observación a qué distancia se sitúa su vecino más cercano. Entonces basta con fijar una ε que permita que una proporción «suficientemente grande» de las observaciones tenga una distancia a su vecino más cercano inferior a ε. Por «suficientemente grande» entendemos el 90-95 % de las observaciones que deben tener al menos un vecino en su ε-vecindad.
¿Cómo implementar el DBSCAN con Python?
El aprendizaje de DBSCAN se facilita con la biblioteca Scikit-Learn. Nuestro conjunto de datos de ejemplo se crea fácilmente con la función make_blobs de Scikit-Learn. Así es como se implementa en código:
Ahora que tenemos nuestro conjunto de datos intentaremos determinar la ε óptima para obtener una mejor partición de nuestro conjunto de datos.
Scikit-Learn proporciona una clase NearestNeighbors que nos permite determinar los vecinos más cercanos de cada observación, así como las distancias. Así es como se implementa en código:
Este es el resultado obtenido:
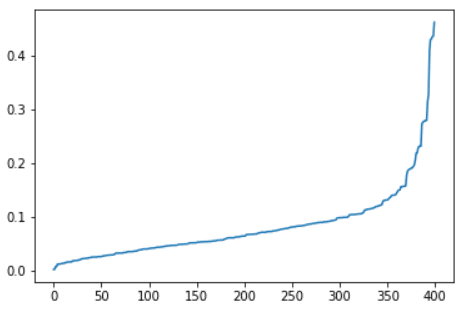
Como hemos visto antes, elegiremos una ε para que el 90 % de las observaciones tengan una distancia de vecindad inferior a ε. En nuestro ejemplo, 0,2 parece adecuado.
Ahora que hemos optimizado nuestra ε podemos realizar nuestra partición utilizando DBSCAN que ya está implementada en Scikit-Learn.
Este es el resultado obtenido:
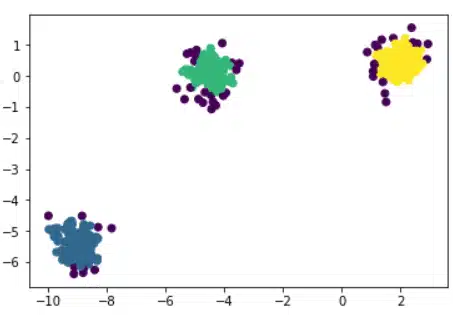
Los argumentos eps y min_samples se utilizan para establecer los parámetros del algoritmo, es decir, la distancia ε y el número mínimo de vecinos que deben considerarse como una observación central.
De esta manera, el algoritmo detectó 3 clústeres principales y algunas anomalías. Cada una de las observaciones se etiqueta con la etiqueta del clúster correspondiente (por ejemplo, 0,1,2). Las anomalías se etiquetan con -1 y, por tanto, forman una clase separada además de los 3 clústeres detectados.
El uso de un algoritmo de clustering como el DBSCAN no es fácil dependiendo de los datos que se tengan. Suele ser necesario repasarlos.