Los Self-Organizing Maps, o SOM, son un tipo de red de neuronas artificiales (ANN) utilizados para el aprendizaje no supervisado. Permiten reducir la dimensionalidad de los datos mientras se preserva su estructura topológica, ofreciendo así una poderosa herramienta para el clustering y la exploración de datos.
A diferencia de las redes de neuronas clásicas, los self-organizing maps funcionan por aprendizaje competitivo en lugar de por corrección de errores e integran una función de vecindad para mantener las relaciones espaciales de los datos.
Origen de los SOM
Los self-organizing maps fueron introducidos en los años 1980 por el investigador finlandés Teuvo Kohonen. Por eso también se les llama mapas de Kohonen o Kohonen maps.
Inspirados en los mecanismos biológicos del cerebro, imitan la manera en que las neuronas organizan y clasifican la información para formar estructuras significativas.
Funcionamiento de los SOM
El aprendizaje de un Self-Organizing Map se basa en un proceso de varios pasos, que le permite transformar datos complejos en una representación organizada y legible. Aquí se detalla un funcionamiento típico, paso a paso, de un SOM.
1. Inicialización de los pesos
Antes de comenzar el entrenamiento, cada neurona del mapa está asociada a un vector de pesos, inicializado de manera aleatoria. Este vector tiene la misma dimensión que los datos de entrada y representa la identidad de cada neurona antes de que sea ajustada por el aprendizaje.
2. Selección de una muestra de entrada
En cada iteración, un vector de entrada es seleccionado aleatoriamente del conjunto de datos de entrenamiento. Este vector representa un punto de datos que el SOM debe aprender a organizar en el mapa.
3. Identificación del Best Matching Unit
Una vez elegida la muestra, el algoritmo busca la neurona cuyos pesos están más cerca de este vector de entrada. Esta proximidad se mide utilizando la distancia euclidiana o norma euclidiana entre el vector de entrada y las neuronas. La neurona más cercana se identifica como el BMU (Best Matching Unit).

4. Actualización de los pesos del BMU y de sus vecinos
Después de encontrar el BMU, el algoritmo ajusta sus pesos para acercarlos al vector de entrada. Sus neuronas vecinas también son actualizadas, pero en menor medida.
La magnitud de esta actualización depende de dos factores principales:
- La tasa de aprendizaje (notada α o alfa) : Alfa controla la velocidad a la que se ajustan los pesos de las neuronas. Disminuye a lo largo de las iteraciones para evitar cambios demasiado bruscos.
- La función de vecindad : La actualización afecta a las neuronas situadas alrededor del BMU, y su magnitud disminuye con la distancia. Una función común es la función gaussiana.
Esta fase permite que el BMU y sus vecinos se acerquen progresivamente a las características de los datos, preservando al mismo tiempo la estructura topológica de las relaciones entre los puntos de datos.
5. Reducción de la tasa de aprendizaje y del vecindario
A medida que avanzan las iteraciones, la tasa de aprendizaje y el tamaño del vecindario disminuyen. Esto permite un ajuste fino de los pesos en las últimas etapas del entrenamiento y garantiza que los datos estén bien organizados en el mapa.
- Al principio, el vecindario es amplio, permitiendo que todo el mapa se organice globalmente.
- Progresivamente, el vecindario se reduce, afinando el mapa y estabilizando los clusters formados.
6. Convergencia y estabilización
El entrenamiento continúa hasta que el mapa alcanza un estado estable, donde los pesos de las neuronas ya no cambian significativamente de una iteración a otra. En esta etapa, cada neurona representa una región específica de los datos de entrada.
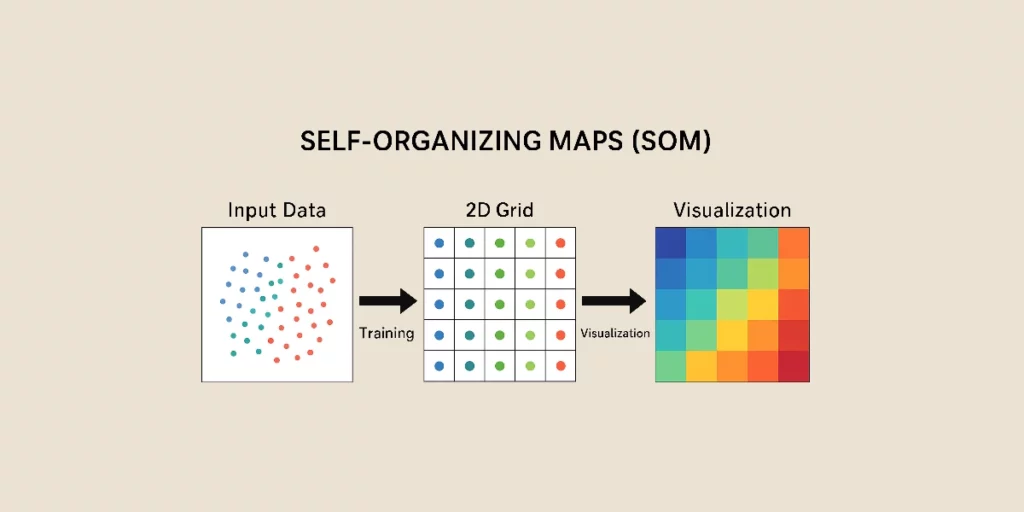
7. Inferencia y visualización de los resultados
Una vez entrenado el SOM, puede ser utilizado para organizar nuevos datos y facilitar su análisis visual. La distancia entre un vector de entrada y los pesos de las neuronas permite determinar dónde se sitúa un nuevo dato en el mapa.
Un método común para visualizar los SOM consiste en asignar colores a las diferentes regiones del mapa. Cuanto más oscuro sea el color, mayor será la concentración de datos.
Los clusters de datos similares aparecen claramente en el mapa, ofreciendo una visualización intuitiva de las relaciones entre las diferentes categorías.
Ventajas y Desventajas de los SOM
Los SOM ofrecen varias ventajas notables. Permiten reducir la dimensionalidad de los datos al tiempo que conservan su organización topológica. Gracias a su representación gráfica intuitiva, facilitan la visualización y la interpretación de conjuntos de datos complejos. A menudo se utilizan para realizar clustering, incluso sin conocer las clases presentes en los datos.
Sin embargo, los SOM tienen ciertas limitaciones. Se adaptan mal a los datos puramente categóricos o mixtos (salvo después de un codificado apropiado), que no siguen una lógica en el espacio de representación. Su tiempo de entrenamiento puede ser largo y su rendimiento depende del ajuste correcto de los parámetros.
Aplicaciones de los SOM
Los SOM se utilizan en diversos dominios para organizar y analizar datos. Por ejemplo, en el sector del marketing, donde permiten agrupar clientes según su comportamiento de compra para optimizar las estrategias comerciales.
En reducción de dimensionalidad, facilitan la cartografía de datos de alta dimensión. Esto permite una mejor comprensión de las relaciones internas en los datos.
En la detección de anomalías, se utilizan para identificar transacciones fraudulentas al identificar los puntos de datos que no corresponden a ningún cluster predefinido.
Para la visualización de datos, ayudan a comprender mejor las poblaciones y las relaciones entre diferentes parámetros. Al transformar un conjunto de datos complejo en una representación 2D, permiten identificar rápidamente tendencias y patrones invisibles en tablas brutas.

Conclusión
Los SOM son una herramienta poderosa para el aprendizaje no supervisado en análisis de clusters, reducción de dimensionalidad y visualización de datos. Tienen limitaciones, en términos de tiempo de entrenamiento y adaptación a datos mixtos. Se utilizan en finanzas, marketing, salud y análisis de imágenes. Su capacidad para revelar estructuras ocultas en los datos los convierte en una elección ineludible para la exploración de datos no etiquetados.