Se dice que un modelo tiene la propiedad de Markov si su estado en un momento T depende únicamente de su estado en el momento T-1. Si podemos observar los estados en los que se encuentra el modelo en cada instante, hablamos de un modelo de Markov observable. De lo contrario, hablamos de un modelo de Markov oculto. En este artículo, ilustraremos estos modelos para comprender su funcionamiento y utilidad.
Definición matemática rigurosa

Matemáticamente, una secuencia de variables aleatorias (Xn) con valores en un espacio de estados E es una cadena de Markov si cumple con la propiedad de Markov débil. Esta propiedad se expresa mediante la siguiente relación:
P(X_{n+1} = i_{n+1} | X_1 = i_1, ..., X_n = i_n) = P(X_{n+1} = i_{n+1} | X_n = i_n) Esta ecuación significa que la probabilidad de transición hacia el estado futuro i_{n+1} solo depende del estado presente i_n, y no de la secuencia completa de estados pasados.
Los elementos clave de una cadena de Markov
El espacio de estados E: el conjunto de todos los estados posibles en los que el sistema puede encontrarse. En nuestro ejemplo meteorológico, E = {sol, nubes, lluvia}.
Las probabilidades de transición: P(X_{n+1} = j | X_n = i) representa la probabilidad de pasar del estado i al estado j en un paso.
La homogeneidad temporal: si estas probabilidades de transición no dependen del tiempo n, se dice que la cadena es homogénea. Es el caso más frecuentemente estudiado.
Esta formalización matemática permite distinguir claramente las cadenas de Markov de otros procesos estocásticos y constituye la base de toda su teoría.
Historia y fundamentos de las cadenas de Markov

Las cadenas de Markov llevan el nombre del matemático ruso Andreí Andreievich Markov (1856-1922), quien introdujo este concepto en 1902 en el marco de sus investigaciones sobre la extensión de la ley de los grandes números a las cantidades dependientes.
Markov se interesó inicialmente en extender los teoremas límite de las probabilidades más allá del caso de las variables aleatorias independientes. Su motivación era comprender cómo la ley de los grandes números podía aplicarse a las secuencias de eventos donde cada evento depende de aquel que lo precede, pero no de todo el historial.
La innovación conceptual
La idea revolucionaria de Markov fue modelar procesos donde el futuro depende del pasado solo a través del presente. Esta propiedad, hoy llamada «propiedad de Markov», puede expresarse de forma intuitiva así: «la historia solo importa por su influencia en el estado actual».
Markov mismo aplicó sus cadenas al análisis de las sucesiones de letras en la literatura rusa, especialmente en la obra «Eugenio Oneguin» de Pushkin, demostrando así que los conceptos matemáticos podían aplicarse a campos no matemáticos.
Desarrollos modernos
Desde su creación, las cadenas de Markov han experimentado un desarrollo extraordinario y se han convertido en una herramienta fundamental en numerosos campos científicos y tecnológicos, desde la física estadística hasta la inteligencia artificial moderna.
Modelo de Markov observable

Consideremos la situación que sigue:
Estás encerrado en casa un día de lluvia y te gustaría determinar el clima que hará en los próximos cinco días.
Como no eres meteorólogo, te simplificas la tarea haciendo la hipótesis de que el clima sigue un modelo de Markov: el clima en el día J depende únicamente del clima en el día J-1.
Para simplificar aún más, consideras que solo hay tres tipos de clima posibles: sol, nubes o lluvia.
Basándote en las observaciones de los últimos meses, estableces el siguiente diagrama de transiciones:

La matriz de transición asociada es

Recordatorio, esta matriz se lee de la siguiente manera:
- La probabilidad de que haya sol mañana sabiendo que hoy llueve es de 35%
- La probabilidad de que haya nubes mañana sabiendo que ya hay hoy es de 25%
Calculemos la probabilidad de que el clima de los próximos cinco días sea “sol, sol, lluvia, nubes, sol”.
Como el clima de un día depende únicamente del clima que hizo el día anterior, basta con multiplicar las probabilidades (recordatorio: hoy llueve):

Podemos calcular esta probabilidad para todas las combinaciones posibles, y seleccionar la combinación con la probabilidad más alta para responder a la problemática.
En nuestro caso, aquí están las 5 combinaciones que tienen más probabilidades de realizarse:

Propiedades fundamentales de la matriz de transición

La matriz de transición que hemos utilizado en el ejemplo anterior posee propiedades matemáticas importantes que conviene entender.
Estructura de la matriz
Una matriz de transición P = (p_{ij}) debe cumplir dos restricciones esenciales:
- Todos los elementos son positivos o nulos: p_{ij} ≥ 0 para todo i, j
- Cada fila suma 1: Σ_j p_{ij} = 1 para todo i
Esta segunda propiedad refleja el hecho de que desde cualquier estado, el sistema debe necesariamente transitar hacia un estado (inclusive permanecer en el mismo estado).
Potencias de la matriz y predicciones a largo plazo
Una de las propiedades más notables es que la matriz P^n (P elevada a la potencia n) proporciona directamente las probabilidades de transición en n pasos. Así, el elemento (P^n)_{ij} representa la probabilidad de pasar del estado i al estado j en exactamente n pasos.
Esta propiedad nos permite hacer predicciones meteorológicas a largo plazo. Por ejemplo, si calculamos P10, obtenemos las probabilidades de transición para 10 días.
Convergencia hacia el equilibrio
Bajo ciertas condiciones, las sucesivas potencias de la matriz P convergen hacia una matriz límite, cuyas filas son todas idénticas. Esta fila común representa la distribución estacionaria del sistema; la distribución de las probabilidades hacia la cual el sistema tiende a largo plazo, independientemente de su estado inicial.
En nuestro ejemplo meteorológico, esto significaría que en el muy largo plazo, la probabilidad de tener sol, nubes o lluvia se vuelve constante y predecible.
Clasificación de los estados en una cadena de Markov

Una vez establecida la matriz de transición, es esencial comprender el comportamiento a largo plazo de cada estado. Este análisis permite clasificar los estados según sus propiedades dinámicas.
Estados transitorios y recurrentes
Un estado se dice transitorio si, partiendo de ese estado, existe una probabilidad no nula de no volver a él nunca. Por el contrario, un estado es recurrente si, partiendo de ese estado, estamos seguros de regresar a él tarde o temprano.
En nuestro ejemplo meteorológico, si modificamos la matriz para incluir un estado «tormenta» del cual solo se puede salir hacia «lluvia» y al que no se puede volver, entonces «tormenta» sería un estado transitorio.
Estados absorbentes
Un estado se dice absorbente si es imposible salir de él una vez que se ha entrado. Matemáticamente, esto significa que p_{ii} = 1 para este estado i.
Ejemplo concreto: en un modelo de duración de vida de un organismo con los estados «juvenil», «adulto», «senescente», y «fallecido», el estado «fallecido» es absorbente porque un organismo muerto no puede cambiar de estado.
Cadenas irreducibles
Una cadena de Markov es irreducible si todos los estados se comunican entre sí, es decir, es posible pasar de cualquier estado a cualquier otro estado en un número finito de pasos.
Nuestro modelo meteorológico es irreducible: podemos pasar del sol a la lluvia (vía las nubes), de la lluvia al sol, etc. Esta propiedad garantiza la existencia de una distribución estacionaria única.
Periodicidad
Un estado tiene un período d si solo se puede regresar a él en instantes múltiplos de d. Si d = 1, el estado se dice aperiódico. Una cadena irreducible y aperiódica siempre converge hacia su distribución estacionaria.
Esta clasificación permite predecir el comportamiento asintótico del sistema y determina qué herramientas matemáticas pueden aplicarse para el análisis.
Distribución estacionaria y convergencia hacia el equilibrio

Hemos mencionado anteriormente el concepto de convergencia hacia el equilibrio. Ahora profundicemos en esta noción fundamental.
¿Qué es una distribución estacionaria?
Una distribución estacionaria π es un vector de probabilidades que permanece inalterado por la dinámica de la cadena. Matemáticamente, verifica la ecuación: π = πP, donde P es la matriz de transición.
En nuestro ejemplo meteorológico, si la distribución estacionaria es π = (0.4, 0.3, 0.3) para (sol, nubes, lluvia), esto significa que a largo plazo, habrá sol el 40% del tiempo, nubes el 30% del tiempo, y lluvia el 30% del tiempo, independientemente del clima de hoy.
Existencia y unicidad
Para una cadena de Markov irreducible en un espacio de estados finito, siempre existe una única distribución estacionaria. Esta propiedad notable garantiza que el sistema tiene un comportamiento predecible a largo plazo.
El teorema ergódico
El teorema ergódico es uno de los resultados más poderosos de la teoría de las cadenas de Markov. Establece que, para una cadena irreducible y aperiódica:
- Convergencia: No importa el estado inicial, las probabilidades convergen hacia la distribución estacionaria
- Ley fuerte de los grandes números: La proporción de tiempo pasado en cada estado converge hacia su probabilidad estacionaria
Concretamente, esto significa que si observamos nuestro clima durante muchos años, la frecuencia observada de cada tipo de tiempo convergerá hacia las probabilidades de la distribución estacionaria.
Aplicaciones prácticas de la ergodicidad
Esta propiedad permite calcular promedios a largo plazo sin simulación exhaustiva. Por ejemplo, si una máquina tiene una probabilidad estacionaria de 0.95 de estar funcional, sabemos que estará disponible el 95% del tiempo a largo plazo, información crucial para la planificación industrial.
La ergodicidad también justifica el uso de las cadenas de Markov en los algoritmos de muestreo Monte Carlo: dejando que la cadena evolucione durante suficiente tiempo, se obtienen muestras según la distribución deseada.
Ejercicios prácticos para dominar las cadenas de Markov

Para consolidar su comprensión, aquí hay algunos ejercicios clásicos con sus soluciones detalladas.
Ejercicio 1: La urna de Ehrenfest
Una urna contiene 4 bolas numeradas. En cada etapa, se saca un número al azar y se mueve la bola correspondiente a la otra urna. El estado del sistema es el número de bolas en la primera urna.
Pregunta: Determine la matriz de transición y calcule la distribución estacionaria.
Solución: Los estados posibles son {0,1,2,3,4}. Si la urna 1 contiene i bolas, la probabilidad de pasar al estado i-1 es i/4 (sacar una bola de la urna 1), y la probabilidad de pasar al estado i+1 es (4-i)/4 (sacar una bola de la urna 2).
La distribución estacionaria sigue una ley binomial: π(i) = C(4,i)/16, es decir, π = (1/16, 4/16, 6/16, 4/16, 1/16).
Ejercicio 2: Caminata aleatoria en un grafo
Un peón se mueve en un cuadrado cuyos vértices son A, B, C, D. En cada etapa, pasa a un vértice adyacente con probabilidad igual.
Pregunta: ¿La cadena es irreducible? ¿Periódica? Calcule el tiempo medio de regreso.
Solución:
- Irreducible: Sí, se puede ir de cualquier vértice a cualquier otro
- Periódica: Sí, de período 2 (se requiere un número par de etapas para regresar al punto de partida)
- Tiempo medio de regreso: 4 etapas para cada vértice
Ejercicio 3: Modelo de duración de vida
Un organismo pasa por los estados: juvenil (J), maduro (M), senescente (S), fallecido (D). La matriz de transición es:
J M S D
J [0.6 0.4 0 0 ]
M [0 0.7 0.3 0 ]
S [0 0 0.8 0.2]
D [0 0 0 1 ]
Pregunta: Calcule la probabilidad de que un individuo juvenil alcance el estado senescente.
Solución: Se debe resolver el sistema de ecuaciones. La probabilidad buscada es de 0.4 × (0.3/0.3) = 0.4, porque todo individuo maduro alcanza inevitablemente el estado senescente.
Ejercicio 4: Tiempo de absorción
Retomemos el ejercicio anterior. Calcule la esperanza de vida de un individuo juvenil.
Solución: Utilizando las ecuaciones de tiempo de absorción, la esperanza de vida de un juvenil es de aproximadamente 8.33 unidades de tiempo.
Estos ejercicios ilustran los conceptos teóricos a través de situaciones concretas y lo preparan para modelar sus propios problemas con las cadenas de Markov.
Extensión a las cadenas de Markov en tiempo continuo

Hasta ahora, hemos estudiado cadenas de Markov en tiempo discreto, donde las transiciones ocurren en instantes regulares (día 1, día 2, etc.). En muchas aplicaciones reales, los cambios de estado pueden ocurrir en cualquier momento: este es el ámbito de los procesos de Markov en tiempo continuo.
Diferencias conceptuales fundamentales
En lugar de matrices de transición, utilizamos generadores infinitesimales que describen las tasas de transición instantáneas. Si q_{ij} representa la tasa de transición del estado i hacia el estado j, entonces la probabilidad de transición durante un pequeño intervalo dt es aproximadamente q_{ij} × dt.
Ejemplo concreto: centro de llamadas
Consideremos un centro de llamadas donde las llamadas llegan según un proceso de Poisson con una tasa λ = 5 llamadas/hora, y cada llamada se procesa en promedio en 10 minutos (tasa de servicio μ = 6 llamadas/hora).
Los estados representan el número de llamadas en curso. Las transiciones son:
- Estado n → Estado n+1 con tasa λ (llegada de una llamada)
- Estado n → Estado n-1 con tasa nμ (fin de procesamiento de una llamada)
Ecuaciones de Chapman-Kolmogorov continuas
La dinámica del sistema está gobernada por la ecuación diferencial: dP(t)/dt = P(t) × Q
donde Q es la matriz generadora y P(t) da las probabilidades de transición en el tiempo t.
Distribución estacionaria en tiempo continuo
En el equilibrio, la condición se vuelve: π × Q = 0, donde π es la distribución estacionaria. Esta ecuación expresa el equilibrio de flujo: para cada estado, la tasa de entrada es igual a la tasa de salida.
Aplicaciones prácticas
- Fiabilidad de sistemas Un equipo puede fallar en cualquier momento (tasa λ) y ser reparado (tasa μ). El proceso continuo modela naturalmente estos eventos imprevisibles.
- Epidemiología Los modelos SIR (Susceptible-Infectado-Restaurado) usan tasas de contaminación y curación continuas para predecir la evolución de epidemias.
- Finanzas cuantitativas Los cambios de precios de activos financieros siguen procesos continuos, modelados por difusiones (extensiones estocásticas de los procesos de Markov).
Ventajas del tiempo continuo
Este enfoque refleja con mayor fidelidad la realidad de muchos fenómenos naturales y permite cálculos analíticos a menudo más elegantes. Además, sirve como puente hacia modelos más sofisticados como los procesos de difusión y las ecuaciones diferenciales estocásticas.
Métodos de Monte Carlo por cadenas de Markov (MCMC)

Las cadenas de Markov encuentran una aplicación revolucionaria en los métodos de muestreo estadístico, especialmente cuando las distribuciones son demasiado complejas para ser muestreadas directamente.
Principio fundamental del MCMC
La idea brillante consiste en construir una cadena de Markov cuya distribución estacionaria sea precisamente la distribución objetivo que queremos muestrear. Al dejar evolucionar la cadena el tiempo suficiente, las muestras obtenidas siguen aproximadamente la distribución deseada.
El algoritmo de Metropolis-Hastings
Este algoritmo universal permite muestrear cualquier distribución π(x), incluso si solo se conoce hasta una constante de normalización.
Funcionamiento:
- A partir del estado actual xₜ, se propone un nuevo estado y según una distribución de propuesta q(y | xₜ)
- Se calcula el ratio de aceptación:
α = min(1, [π(y) q(xₜ | y)] / [π(xₜ) q(y | xₜ)]) - Se acepta y con probabilidad α, si no, se permanece en xₜ
Este procedimiento garantiza que la distribución estacionaria de la cadena generada sea exactamente π(x).
Aplicaciones en estadística bayesiana
En la inferencia bayesiana, a menudo queremos muestrear la distribución posterior de los parámetros. Si tenemos datos D y parámetros θ con una prior π(θ), la distribución posterior es:
π(θ | D) ∝ π(D | θ) × π(θ)
El MCMC permite muestrear esta distribución incluso cuando no tiene una forma analítica simple, revolucionando así el análisis estadístico moderno.
Muestreo de Gibbs
Caso particular del algoritmo Metropolis-Hastings para distribuciones multivariadas. En lugar de actualizar todos los parámetros simultáneamente, se actualiza uno por uno, condicionando sobre los demás.
Este método es especialmente eficaz para modelos gráficos como las redes bayesianas, donde las distribuciones condicionales suelen tener formas simples.
Diagnóstico de convergencia
Uno de los principales retos del MCMC es determinar cuándo la cadena ha “olvidado” su estado inicial y comienza a muestrear realmente la distribución estacionaria. Algunos diagnósticos habituales:
- Visualización de las trazas temporales
- Criterio de Gelman-Rubin (comparación entre múltiples cadenas)
- Pruebas de autocorrelación
Aplicaciones contemporáneas
- Inteligencia artificial: las redes neuronales bayesianas usan MCMC para cuantificar la incertidumbre en las predicciones, algo crucial en entornos críticos.
- Epidemiología computacional: modelos de propagación de epidemias con parámetros inciertos se calibran por MCMC con base en datos reales.
- Finanzas cuantitativas: la estimación de modelos de volatilidad estocástica y la valoración de opciones complejas dependen ampliamente del MCMC.
El MCMC es un ejemplo perfecto de cómo un concepto matemático fundamental —las cadenas de Markov— se convierte en una herramienta computacional revolucionaria para la ciencia de datos moderna.
Cadenas de Markov en el ecosistema moderno de la ciencia de datos

En la era del big data y la inteligencia artificial, las cadenas de Markov han encontrado nuevos campos de aplicación que van mucho más allá de su marco teórico original.
Procesamiento automático del lenguaje natural (NLP)
Los modelos de lenguaje basados en cadenas de Markov fueron los precursores de arquitecturas modernas como GPT. Modelan la probabilidad de aparición de una palabra según las anteriores, permitiendo:
- Generación automática de texto: encadenando las probabilidades de transición, se generan frases coherentes
- Corrección ortográfica: detectan secuencias improbables de caracteres
- Clasificación de textos: cada clase (spam/no spam) tiene su propio modelo markoviano
Sistemas de recomendación
Plataformas como Netflix o Spotify utilizan cadenas de Markov para modelar el comportamiento de los usuarios:
- Estados: contenidos visualizados o escuchados
- Transiciones: probabilidad de pasar de un contenido a otro
- Objetivo: predecir qué contenido interesa más al usuario a continuación
Análisis de secuencias temporales en IoT
En el Internet de las Cosas, los sensores generan flujos secuenciales de datos. Las cadenas de Markov permiten:
- Detección de anomalías: identificar secuencias inusuales de medidas
- Mantenimiento predictivo: anticipar fallos en equipos industriales
- Optimización energética: modelar patrones de consumo
Ciberseguridad y detección de fraudes
Los analistas de seguridad aplican cadenas de Markov para:
- Detección de intrusiones: modelar comportamientos normales de usuarios y detectar desviaciones
- Análisis de malware: las secuencias de llamadas al sistema revelan firmas maliciosas
- Autenticación por comportamiento: identificar usuarios a partir de sus patrones de navegación
Marketing digital y analítica web
Las cadenas de Markov optimizan la experiencia en sitios web:
- Análisis de recorrido del cliente: entender los caminos hacia la conversión en e-commerce
- A/B testing secuencial: evaluar el impacto de cambios en el comportamiento de navegación
- Atribución de marketing: medir la eficacia de los canales de adquisición
Bioinformática computacional
Más allá del análisis clásico del ADN, sus usos actuales incluyen:
- Análisis de expresión génica: modelar la evolución temporal de la actividad de los genes
- Epidemiología genómica: rastrear la propagación de variantes víricas mediante secuencias
- Medicina personalizada: predecir la evolución de enfermedades a partir de biomarcadores
Integración con el aprendizaje automático
Las cadenas de Markov se combinan con técnicas modernas de IA:
- Feature engineering: crear variables explicativas a partir de secuencias
- Reinforcement learning: los procesos de decisión markovianos son su fundamento teórico
- Redes neuronales recurrentes: LSTM y GRU generalizan las cadenas de Markov con memoria adaptativa
Estas aplicaciones demuestran que las cadenas de Markov, lejos de ser un concepto puramente académico, son hoy un pilar metodológico clave para extraer valor de los datos secuenciales en la economía digital moderna.
Modelo oculto de Markov

Mantenemos las mismas hipótesis que en la parte anterior.
Imagina que un psicópata del clima te encierra en una habitación sin ventanas, con solo una computadora y una lámpara. Cada día, la lámpara se enciende de un color distinto según el clima. Tu captor te da la siguiente matriz de observación:
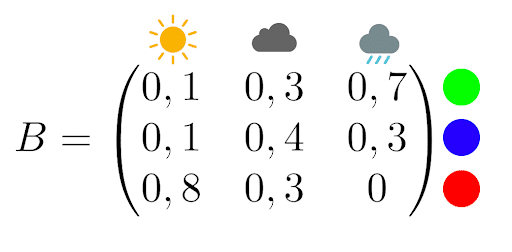
Por ejemplo, si llueve, hay un 70 % de probabilidad de que la lámpara se encienda en verde y un 30 % de que sea azul.
Puedes volver a casa si logras determinar el tiempo que hará durante los próximos cinco días, únicamente observando el color de la lámpara. Decides entonces construir un modelo oculto de Markov.
Permaneces encerrado cinco días y anotas la siguiente secuencia de colores:
azul, azul, rojo, verde, rojo
Recuerdas que el día anterior al encierro estaba lloviendo.
Puedes entonces escribir un código en Python que calcule la secuencia de estados meteorológicos más probable:
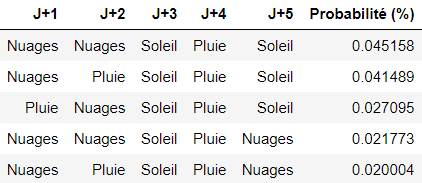
Nota: También se podría haber implementado el algoritmo de Viterbi, que habría devuelto la secuencia más probable:
[‘Nublado’, ‘Nublado’, ‘Soleado’, ‘Lluvia’, ‘Soleado’]
Este tipo de predicción es interesante, aunque bastante básica. Si quieres aprender a hacer predicciones mucho más potentes —por ejemplo, con algoritmos de machine learning— descubre nuestros cursos en data science.
Profundización en los Modelos Ocultos de Markov (HMM)

El ejemplo del “psicópata meteorológico” introduce los HMM de forma lúdica, pero estos modelos merecen una exposición más técnica: son una de las herramientas más potentes del aprendizaje estadístico moderno.
Estructura matemática de un HMM
Un modelo oculto de Markov se compone de tres elementos fundamentales:
- Estados ocultos: la secuencia de estados no observables (por ejemplo, el clima real)
- Observaciones: lo que podemos medir (por ejemplo, el color de la lámpara
- Dos matrices de probabilidad:
- La matriz de transición entre estados ocultos A
- La matriz de emisión/observación B
Los tres problemas fundamentales de los HMM
La teoría de los HMM gira en torno a tres preguntas clave:
Problema 1: Evaluación
¿Cuál es la probabilidad de observar una secuencia dada?
El algoritmo Forward permite calcular esta probabilidad eficientemente, evitando la explosión combinatoria.
Problema 2: Decodificación
¿Cuál es la secuencia de estados ocultos más probable?
El algoritmo de Viterbi lo resuelve mediante programación dinámica. En nuestro ejemplo meteorológico, determina la secuencia de climas más verosímil dada la secuencia de colores observados.
Problema 3: Aprendizaje
¿Cómo estimar los parámetros del modelo a partir de observaciones?
El algoritmo de Baum-Welch (una variante del algoritmo EM) optimiza iterativamente las matrices A y B para ajustar el modelo a los datos.
Aplicaciones avanzadas de los HMM
- Reconocimiento automático del habla: Los fonemas son los estados ocultos; los espectrogramas de audio, las observaciones. Los HMM modelan cómo cada fonema genera características acústicas.
- Análisis de secuencias biológicas: En bioinformática, los HMM detectan genes en secuencias de ADN: las regiones codificantes/no codificantes son los estados ocultos; los nucleótidos (A, T, G, C), las observaciones.
- Finanzas cuantitativas: Los regímenes de mercado (alcista/bajista) son estados ocultos; los rendimientos financieros, observaciones. Los HMM ayudan a detectar cambios de régimen y ajustar las estrategias de inversión.
Límites y extensiones
Los HMM clásicos suponen que las observaciones son independientes dado el estado oculto.
Extensiones como los HMM jerárquicos o las redes neuronales recurrentes (RNN) superan esta limitación, permitiendo modelos más expresivos y contextuales.
Aplicaciones prácticas de las cadenas de Markov

Más allá de la predicción meteorológica, las cadenas de Markov tienen aplicaciones en numerosos campos concretos:
PageRank y motores de búsqueda
El algoritmo PageRank de Google usa una cadena de Markov para clasificar páginas web.
- Cada página es un estado
- Los enlaces son transiciones
- La importancia de una página se define por su probabilidad en la distribución estacionaria de la cadena
Finanzas y seguros
Las aseguradoras de automóviles utilizan cadenas de Markov en sus sistemas de bonus-malus:
- El estado representa la clase de bonificación del conductor
- Las transiciones dependen del número de siniestros
- Esto permite calcular las primas de forma actuarial y dinámica
Bioinformática y genética
Las cadenas de Markov modelan la relación entre nucleótidos sucesivos en secuencias de ADN. Los HMM son claves para:
- Identificar genes
- Predecir estructuras de proteínas
- Detectar regiones codificantes en el genoma
Fiabilidad industrial
En la industria, las cadenas de Markov modelan el ciclo de vida de sistemas técnicos:
- Estados como «funcional», «en mantenimiento», «averiado»
- Sirven para calcular la disponibilidad de equipos, planificar el mantenimiento preventivo y optimizar los costes
Inteligencia artificial moderna
Los chatbots y generadores de texto usan cadenas de Markov para predecir la siguiente palabra en una frase. Incluso los teclados predictivos de los smartphones aplican este principio para sugerir palabras según el contexto de escritura.
Teoría de colas
Los centros de atención telefónica, bancos o servidores informáticos se modelan como cadenas de Markov, donde cada estado representa el número de usuarios en espera. Este enfoque permite optimizar los recursos y reducir los tiempos de espera.
Para ir más lejos: referencias esenciales

La teoría de las cadenas de Markov es un campo matemático vasto, con una literatura académica sólida. Aquí tienes una selección de referencias imprescindibles para profundizar tus conocimientos.
Libros de referencia fundamentales
- Norris, J.R. – Markov Chains (Cambridge University Press, 1997) Considerada la referencia moderna sobre cadenas de Markov. Cobertura rigurosa y accesible. Esencial para una comprensión matemática sólida.
- Sericola, Bruno – Chaînes de Markov – Théorie, algorithmes et applications (Hermès/Lavoisier, 2013) Obra francesa muy apreciada por su enfoque práctico y sus algoritmos detallados.
- Baldi, Paolo et al. – Martingales et chaînes de Markov. Théorie élémentaire et exercices corrigés (Hermann, 2001) Excelente para el autoaprendizaje, con ejercicios progresivos resueltos.
Especialización por dominio de aplicación
- Méléard, Sylvie – Modèles aléatoires en écologie et évolution (Springer, 2016) Aplicaciones en biología y ecología: modelos estocásticos de poblaciones con cadenas de Markov.
- Brémaud, Pierre – Markov Chains, Gibbs Fields, Monte Carlo Simulation, and Queues (Springer, 1998) Referencia técnica clave para colas de espera y métodos MCMC.
Artículos fundacionales históricos
- Markov, A.A. – Extension of the law of large numbers to dependent quantities (1906) El artículo original donde se introduce el concepto. Disponible traducido en el Journal Électronique d’Histoire des Probabilités et de la Statistique.
Recursos pedagógicos complementarios
- Grinstead, Charles M. & Snell, J. Laurie – Introduction to Probability (AMS) Excelente capítulo dedicado a las cadenas de Markov, con enfoque pedagógico y ejercicios interactivos en línea.
- Ejercicios interactivos – Universidad de Niza Sophia Antipolis Práctica con correcciones automáticas vía la plataforma WIMS: ideal para entrenarse de forma progresiva.
Recursos digitales modernos
- Philippe Gay – Markov y la Bella Durmiente (Images des Maths, 2014)
Artículo de divulgación brillante que presenta los desafíos contemporáneos de las cadenas de Markov de forma accesible.
Estas referencias te permitirán avanzar desde una introducción básica hasta los aspectos más técnicos y aplicados, en función de tus objetivos y áreas de interés.