Le test du khi2 (ou chi-squared) est un test statistique pour des variables prenant un nombre fini de valeurs possibles (donc des variables catégorielles). Pour rappel, un test statistique est une méthode permettant d’accepter ou non une hypothèse, appelée hypothèse nulle, selon son adéquation aux données.
À quoi sert le test du khi-2 ?
L’avantage du test khi-deux est sa grande diversité d’utilisation :
- Test d’adéquation à une loi ou une famille de lois définies à priori, par exemple : la taille d’une population suit-elle une loi normale ? :
- Test d’indépendance, exemple : la couleur des cheveux est elle indépendante du sexe ?
- Test d’homogénéité : deux séries de données sont-elles identiquement distribuées?
Comment fonctionne le test ?
Son principe est de comparer la proximité ou l’éloignement entre la loi de l’échantillon et une loi théorique, avec la statistique dite de Pearson \chi_{Pearson} [\latex], basée sur la distance du khi-2.
Premier problème : Ne disposant que d’un nombre limité de données, nous ne pouvons pas connaître parfaitement la loi de l’échantillon, mais seulement une approximation de celle-ci, la mesure empirique.
La mesure empirique \widehat{\mathbb{P}}_{n,X} [\latex] représente la fréquence des différentes valeurs observées :
Formule mesure empirique
avec
Formule statistiques de Pearson
Sous l’hypothèse nulle , c’est à dire qu’on a bien égalité entre la loi de l’échantillon et la loi théorique, cette statistique de Pearson va converger vers la loi du khi-2 à d degrés de libertés. Le nombre d de degrés de libertés dépend des dimensions du problème, en général c’est le nombre de valeurs possibles -1.
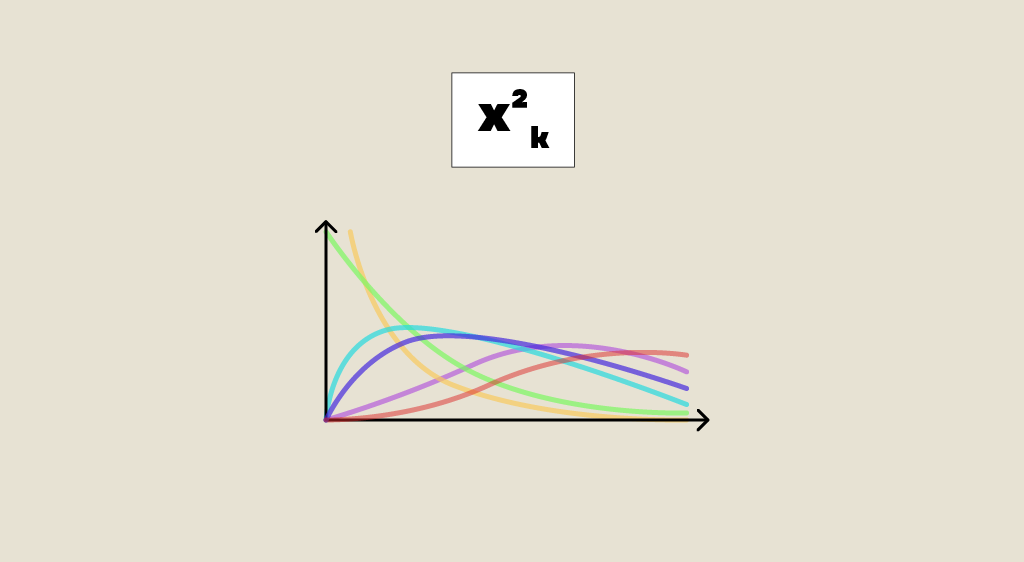
Pour rappel, la loi du khi-2 à d degrés de libertés
centrées réduites indépendantes.
est celle d’une somme de carrés de d gaussiennes
Sinon, cette statistique va diverger à l’infini, ce qui traduit l’éloignement entre des distributions empiriques et théoriques.
Formule limite
Quels sont ses avantages ?
On dispose donc d’une règle de décision simple : si la statistique de Pearson dépasse une certain seuil, on rejette l’hypothèse de départ (la distribution théorique ne colle pas aux données), sinon on l’accepte. L’avantage du test Khi-2 est que ce seuil dépend seulement de la loi du Khi2 et du niveau de confiance alpha, il est donc indépendant de la loi de l’échantillon.
Une application, le test d’indépendance :
Prenons un exemple pour illustrer ce test : on veut savoir si les sexes des deux premiers enfants X et Y d’un couple sont indépendants ?
On a rassemblé les données dans une table de contingence :
La Statistique de Pearson va déterminer si la mesure empirique de la loi conjointe (X,Y) est égale au produit des mesures empiriques marginales, ce qui caractérise l’indépendance :
Ici Observation(x,y) est la fréquence de la valeur (x,y) :
Par exemple:
Ainsi la probabilité théorique pour(fils,fils) est:
Calculons la statistique du test via le code python suivant :
Dans notre cas, les variables X et Y ont seulement 2 valeurs possibles : filles ou garçons, la dimension du problème est donc de (2-1)(2-1) soit 1.
On compare donc la statistique du test au quantile du khi2 à 1 degré de liberté, via la fonction chi2.ppf de scipy.stats. Elle est inférieure au quantile, et la p-valeur supérieure au niveau de confiance = 0.05, on ne peut pas rejeter l’hypothèse nulle avec un confiance 95%,et l’on conclut donc à l’indépendance du sexe des 2 premiers enfants.
Quelles sont ses limites ?
S’il semble très pratique, le test du khi-2 connaît cependant des limites : il constate seulement l’existence de corrélations, mais ne détecte ni l’intensité de celles-ci ni des causalités.
Il repose sur l’approximation de la loi du khi2 avec la statistique de Pearson, vérifiée seulement si l’on dispose d’un nombre suffisant de données. Dans la pratique cette condition de validité est la suivante :
Le test exact de Fisher permet de pallier ce défaut mais nécessite une puissance calcul élevée (dans la pratique, on le limite au cas tables contingences 2*2).
Les tests statistiques sont essentiels en Data Science pour vérifier la pertinence des variables explicatives et valider les hypothèses de sa modélisation. Vous pourrez retrouver davantage d’informations sur le khi-2 et d’autres tests statistiques dans notre module 104 – Statistiques Exploratoires.