Restricted Boltzmann Machines (RBM) are a form of artificial neural network crafted for unsupervised learning, enabling the learning of a probability distribution from a set of input data.
Initially developed by Geoffrey Hinton and Terry Sejnowski in 1985 and gaining popularity in the 2000s, RBMs excel in dimensionality reduction, feature extraction, and imputing missing data. They frequently serve as foundational components for deeper architectures like Deep Belief Networks (DBN).
What is the origin of RBMs?
RBMs are a simplified form of Boltzmann Machines (BM), which are energy-based neural networks with fully interconnected neurons. In contrast, RBMs restrict connections between neurons within the same layer, simplifying calculations and training. This restriction empowers RBMs to capture meaningful latent representations in fields such as computer vision, natural language processing, and content recommendation.
How do RBMs work?
Restricted Boltzmann Machines (RBM) operate through a distinct architecture consisting of two neuron layers: a visible layer representing the input data and a hidden layer that extracts key features. Unlike conventional neural networks, they lack an output layer, focusing instead on modeling a data probability distribution. Learning is achieved by adjusting the weights between these two layers, without any intra-layer connections.
1. Architecture of an RBM
RBMs are structured as symmetric bipartite graphs where each neuron in the visible layer connects with every neuron in the hidden layer, lacking any roadmaps for intra-layer connections. Each connection carries a weight, updated during training.
2. Learning Phase
During learning, a technique known as Contrastive Divergence (CD-k) is employed for weight updates. The process begins by introducing an input vector to the visible layer, which relays information to the hidden layer via a sigmoid activation function. A new sample is subsequently generated from the hidden layer to reconstruct an estimate of the initial input. The variance between this reconstruction and the original input guides the adjustment of model weights. This iterative process continues until the weight updates become negligible.

3. Energy Function and Probability Distribution
RBMs utilize an energy function to calculate the probability of a specific state. The joint probability of the visible and hidden layers follows the Boltzmann distribution.
The Boltzmann distribution formula specifies the probability Ρ(Ε) of a particle residing in an energy state Ε at a temperature Τ. It is articulated as follows:
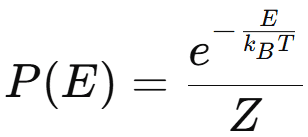
Where:
- P(E) represents the state probability of energy E,
- E is the state’s energy,
- kB is the Boltzmann constant,
- T denotes the temperature in kelvins,
- Z represents the partition function
Thus, a state is more probable when its energy is lower.
4. Weight Update
The neuron connection weights are updated by minimizing the reconstruction error. The update rule is expressed as:
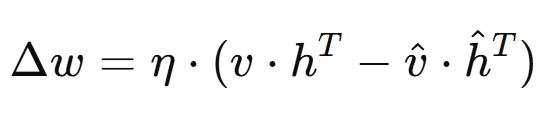
where Δω represents the weight adjustment, η is the learning rate, v and h are the visible and hidden neuron activations, respectively, and v̂ and ĥ are the reconstructed activations. This adjustment refines the weights to diminish the error between actual and reconstructed activations.
What are the advantages and disadvantages of RBMs?
1. Advantages
RBMs offer several benefits. Notably:
- Unsupervised Learning: Their operation through unsupervised learning makes RBMs particularly adept at feature extraction from raw data.
- Ability to model complex and high-dimensional data: They excel at modeling intricate, high-dimensional distributions.
- Serve as foundational blocks in deep architectures (DBN): They are integral to developing deeper architectures like Deep Belief Networks.
2. Disadvantages
- Challenge in identifying optimal hyperparameters: The learning rate must be finely tuned; too high a rate might cause oscillations and hinder convergence, while too low a rate significantly slows learning. Moreover, the number of hidden neurons greatly affects the model’s capacity to capture relevant representations. An insufficient number limits the richness of extracted features, whereas too many risk overfitting.
- Lengthy training process for large datasets: A substantial iteration count necessary for apt weight adjustments poses constraints, especially with large datasets needing numerous computational operations for each weight update.

How are RBMs used?
Restricted Boltzmann Machines find applications across diverse fields:
- Collaborative filtering: Applied in recommendation systems to forecast user preferences.
- Computer vision: Employed in object recognition, image restoration, and noise reduction.
- Natural language processing: Utilized for language modeling, text categorization, and sentiment analysis.
- Bioinformatics: For protein structure prediction and gene expression analysis.
- Finance: Used in stock price forecasting, risk management, and fraud detection.
- Anomaly detection: Applied in fraud transaction identification, network observation, and medical diagnostics.
RBMs’ applicability spans various domains: in recommendation systems, they refine collaborative filtering to predict user preferences; in computer vision, they assist in object detection, image noise reduction, and visual data reconstruction; for natural language processing, they contribute to language modeling, sentiment analysis, and text classification. They also play roles in bioinformatics, notably for gene expression analysis and protein structure prediction, as well as in finance for stock predictions and fraud prevention. Lastly, they are deployed in cybersecurity and medical diagnostics to identify anomalies and detect atypical behaviors.
Conclusion
Restricted Boltzmann Machines are formidable tools for unsupervised learning and feature extraction. Their capacity to learn meaningful representations renders them invaluable for a myriad of artificial intelligence applications. Despite training and parameterization challenges, they remain crucial in creating advanced models like Deep Belief Networks and other deep neural architectures.










