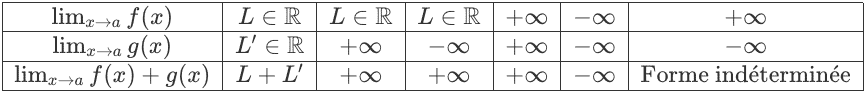All scientific disciplines are based on mathematics, and data science is no exception. When the problems to be solved are optimization problems, you need to know what the limit of a function is. In this article, you'll discover how to determine the limit of a function.
Limit: Definition
The limit of a function f is the value the function approaches when its argument approaches a certain value.
Mathematically, we write
\lim \limits_{x \to a} f(x) = l
We say that f tends towards l when x tends towards a.
Depending on the case, a and l may be real numbers, or equal to \pm \infty.
Limits of standard functions
- Real-valued finite limits
For example, for f(x) = x^2, the limit when x tends towards 2 is 2^2 = 4.
- Infinite limits
When the function is well defined at a real number a (it is said to be continuous at a), then the limit at a is exactly f(a).
When the variable x takes on very large values (positively or negatively), we say that x tends towards more or less infinity. In this case, we distinguish between cases where f(x) approaches a finite value and those where f(x) moves away towards infinity. In the former case, f is said to converge, and in the latter, f to diverge.
Below is a table summarizing the limits of common functions at infinity.
When a function admits a finite limit l \in \mathbb{R} when x \to \infty, then we say that f admits a hor
- Infinite limits at a finite value
\begin{array}{|c|c|}
\hline \text{Function} & \text{Limit} 0, \: x \to 0 \\
\hline f(x) = \frac{1}{x} & \begin{cases} & +\infty \text{ si } x \gt 0 \\ & \infty \text{ si } x \lt 0 \end{cases} \\
\hline nan & nan \\
\hline f(x) = \ln(x) & -\infty \\
\hline f(x) = \sqrt{x} & 0 \\
\hline
\end{array}
When \lim_{x \to a} f(x) = \pm \infty, with a a real number, then the curve of f is said to have a vertical asymptote at a. In other words, the curve moves closer and closer to the straight line with equation x=a.
Limit operations
In most cases, it is possible to perform limit operations to determine the limit.
Limit of a sum of two functions
Limit of a product of two functions
Limit of a quotient of two functions
Click on the tables to display them full-screen.
Determining a limit in practice
To determine limits, it's sometimes simpler to use other functions.
Comparing functions allows you to compare their limits, when they exist.
Comparing functions allows you to compare their limits, when they exist.
There are two main properties for comparing functions
- Comparison theorem
Let f and g be two functions defined on an interval I = [a, +\infty[.
Assume that for any x \in I ; f(x) \geq g(x)
Assume that for any x \in I ; f(x) \geq g(x)
If \lim_{x \to +\infty}g(x) = +\infty, so \lim_{x \to +\infty}f(x) = +\infty
If \lim_{x \to +\infty}f(x) = -\infty, so \lim_{x \to +\infty}g(x) = -\infty
- Gendarme theorem
Let f, g and h be three functions
Assume that for any x \in I ; g(x) \leq f(x) \leq h(x)
If g and h tend to the same limit l in +\infty, then \lim_{x \to +\infty}g(x) = +\infty
You now know what a limit is and how to calculate it. Calculating limits allows you, for example, to define the derivative of a function as the limit of a rate of increase.
If you'd like to discover all the mathematical concepts involved in data science, we invite you to take a look at our curricula.
Facebook
Twitter
LinkedIn
