To define a predictive model, data scientists rely on multiple observations. However, while studying these observations leads to an optimal outcome, data experts often have limited time to analyze all the hypotheses. So how do you find the right model in the least amount of time? This is where Bayesian optimization comes in. What is it? How does it work? The answers are here.
What is the Bayesian approach?
Bayesian optimization directly stems from Bayes’ theorem:
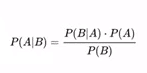
Through this theorem, you have a value y that is a function of x. The idea is to determine the value of x by optimizing the value of y. Here, x consists of a set of parameters (or observations).
Concretely, this can be applied in a multitude of situations, such as setting an ideal price to maximize margins, configuring an application or a database to maximize its performance, managing parameters to optimize supervised learning, etc.
In all these hypotheses, data scientists have a limited number of observations to achieve an optimal result (whether due to time, financial, or material constraints).
Indeed, to define the best model, it usually requires testing numerous hypotheses, performing several trainings and validations. But all these testing phases take time. It is not possible to study an unlimited number of hypotheses.
To address these constraints, Bayesian optimization was implemented.
How does Bayesian optimization work?
The central idea of Bayesian optimization is to minimize the number of observations while quickly converging to the optimal solution. To do this, it is necessary to know three fundamental principles.
The Gaussian process
The idea of the Bayesian approach is to leverage known observations to infer probabilities of events that have not been observed yet. To reach this conclusion, it is necessary to determine the probability distribution for each value X.
For this, the most effective method is undoubtedly the Gaussian process. It allows identifying the most probable value (called mean µ) and the likely dispersion of the value around the mean (called standard deviation σ). This standard deviation σ decreases as you approach an already observed point.
Ideally, you would calculate these values and distances for each observation point. But in practice, this exhaustive representation is not possible due to time constraints. Therefore, it is necessary to select the points to evaluate.
Exploration and exploitation
To design an efficient predictive model, data scientists must define the most relevant points. This happens in two phases:
- Exploration: this is interesting when the standard deviation is particularly large. In other words, the unknown variable in the search space is significant. This allows for testing multiple models and improving the understanding of the function to be optimized.
- Exploitation: at this stage, it is about refining the models previously tested. The idea is to find the maximum or optimal point. To do this, data scientists exploit the mean µ. If it is situated at the extremes, it is easier to identify the right model.

Be careful, it is important to find the right balance between exploration and exploitation. Indeed, if you favor exploration, you risk overlooking other potentially more efficient models. Conversely, if you favor exploitation, you might miss necessary improvements.
The acquisition function
The acquisition function allows finding the right compromise between these two variables. Indeed, for each point in the search space, the function identifies a potential for optimization. Among all these points, the function identifies a maximum. This is the next point to test. You just need to repeat the calculation as many times as necessary until you achieve a convergence between the maximum and the minimum. This pair of parameters is the one that should allow reaching the best performance.
Good to know: Noise can alter the data and make learning more difficult. To avoid this situation, it is crucial to ensure that the environment is stable enough and the observations are reproducible before using Bayesian optimization.
How to put Bayesian optimization into practice?
To simplify Bayesian optimization calculations, it is easiest to use good tools, such as the Python package scikit-optimize or bayesian-optimization. You just need to define a search space, and the tool will then find the high-potential points, notably thanks to the Gaussian process. Again, you will need to relaunch Python until a satisfactory result is obtained.










