As their name suggests, optimization algorithms are designed to find an optimal (or ideally the best) solution to a problem, according to specific criteria or objectives.
Among the many optimization algorithms available, some are inspired by nature: these are known as biomimetic algorithms. They may draw from the collective intelligence of insects (swarm optimization) or the principles of natural selection, as seen in genetic optimization algorithms (also referred to as evolutionary algorithms).
The principles of natural selection, which primarily derive from Darwin’s theory, focus on selecting the most well-adapted individuals, enabling species to evolve over generations.
In the realm of genetic algorithms, the data for our problem are organized in the form of a vector that represents the genome of different individuals. The aim is to create an initial population of individuals and then select the best ones, generation after generation. This selection is based on rating criteria, with the highest-rated individuals chosen for the next generation.
To illustrate this article, consider the example of a vacationer planning to spend 10 days in the Morvan Regional Natural Park in Burgundy. The goal is to visit cities boasting the most historical points of interest while covering the fewest kilometers. On the third and eighth days, accommodations must include a hotel with at least a 3-star rating.
There are certainly more sophisticated turnkey libraries available to implement these algorithms, but the code example developed here will help clarify their basic mechanisms.
The Data
For data collection, I sourced historical points of interest (POIs) for each town in the park from OpenStreetMap. Information from the French government provided the locations of 3-star or better hotels and the geographical coordinates of town centers for calculating distances.

Creating the Initial Population
If our goal were to directly find the optimal solution to the problem, it would involve evaluating all possible combinations and assessing their effectiveness in solving the problem. Unfortunately, current computational capabilities don’t allow for this with complex problems. Hence, we need to form a population large enough to be a representative sample, yet not so large as to excessively prolong computation times. A potential compromise could be a smaller population size in exchange for increasing the number of iterations (or generations). This step involves some experimentation, and multiple tries may be necessary to find a satisfactory compromise. I opted for an initial population of 1500 individuals.
Regarding each individual’s genetic traits, the solution is straightforward: the genome is randomly generated from various values.
In our scenario, a function generates random lists based on the INSEE codes of the various municipalities in the Morvan park.
Evaluating Individuals
Once the first generation of the population is established, each individual must be evaluated to select the best ones.
Here, no one-size-fits-all solution exists; each problem requires its own evaluation strategy to identify the top performers. Once evaluation is complete, the process of selecting and forming new generations begins.
In my case, the two evaluation criteria are the total distance traveled and the total number of points of interest on the route. To avoid routes with few kilometers but lacking points of interest (or the reverse), I chose to group the most efficient routes in terms of both mileage and points of interest by decile. Thus, routes rated 2 belong simultaneously to the second deciles of these two categories. Routes rated 10 include, beyond their deciles, all routes not meeting this dual decile requirement.
As the accommodation criterion inevitably changes with iterations, I decided not to include it as a pure rating criterion but rather use it as a filter within my data frames.
Selection and Creation of the Next Generation
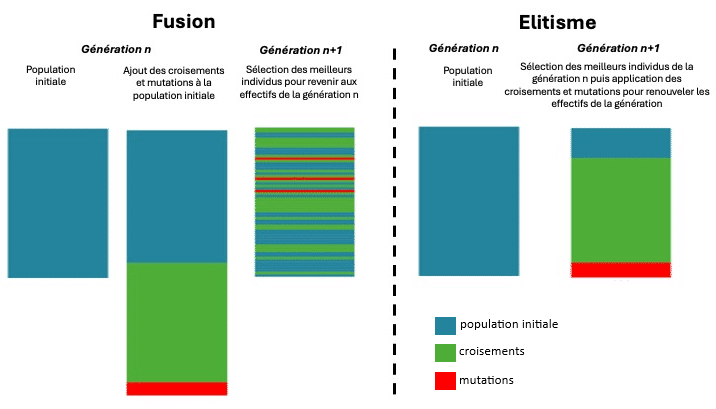
At this stage, two strategies are available: Elitism or fusion. In both scenarios, the aim is to develop a new generation that matches the previous generation in terms of the number of individuals.
With elitism, evaluation occurs first, and the genomes of the most highly-rated individuals are directly reused for the subsequent generation. The remainder of the population is filled with individuals generated through crossover (as in sexual reproduction) or mutations.
In fusion, the new generation (equivalent in number to the previous one) is created first via crossover and mutations. Selection is then applied to retain only the highest evaluated individuals up to the previous generation’s numbers.
For my project, I chose the elitist system, adhering to the old saying that you don’t change a winning team. More seriously, each system offers its own pros and cons. While fusion can expand genetic diversity among individuals, elitism can preserve the best-adapted individuals. This quality persuaded me to choose elitism. For the cohort, I selected 20% of the best individuals in the population as the elite to guide the next generation. Generally, the proportion of elites ranges between 5% and 20%; I opted for the higher range.
Crossover and Mutation
These natural processes enable the creation of new individuals whose distinctive genome traits might better adapt them to their environment. Being better adapted, these individuals will have a higher probability of survival, hence reproduce and pass on their genes.
In genetic algorithms, the concept is similar. The top-evaluated individuals are selected for the subsequent generation and in turn have a greater chance of propagating their traits.
Crossover recreates the mechanics of sexual reproduction. Genes from both parents are blended to form a new, unique genome.
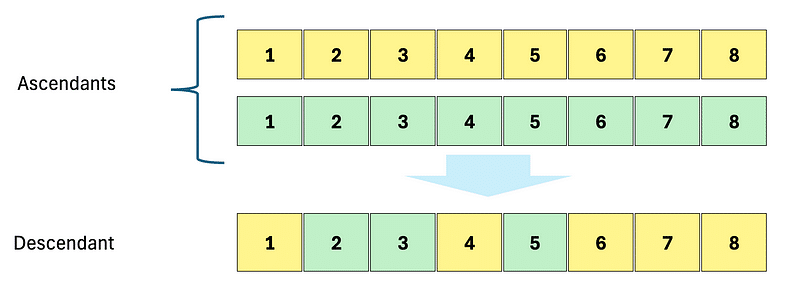
In some models, the suggestion is to combine genomes segment by segment (by halves or gene pairs). For my approach, I favored a method more akin to nature, handling it gene by gene.
In my setup, the crossover function for individuals is combined with a small degree of mutation. Theoretically, at any point, selection happens only between the genes of each parent. With this system, the same city could end up appearing twice in the same route, which is undesirable. Therefore, I added a restriction to prevent this scenario.
In nature, there are also mutation processes where an individual’s genome changes independently of any reproductive process. This mechanism enhances genetic diversity by introducing novel genetic solutions.
Three mutation possibilities may occur.
Insertion: a gene moves to insert after another
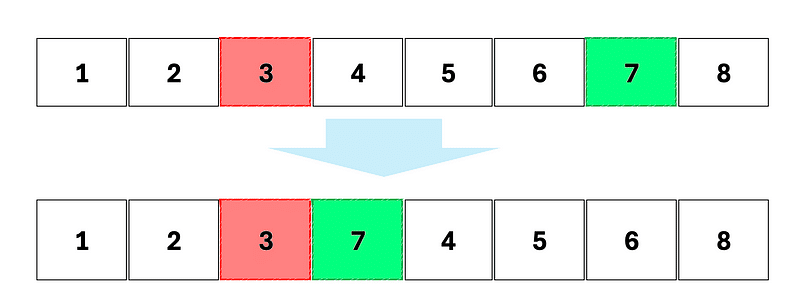
Permutation (or swap): two genes exchange their positions
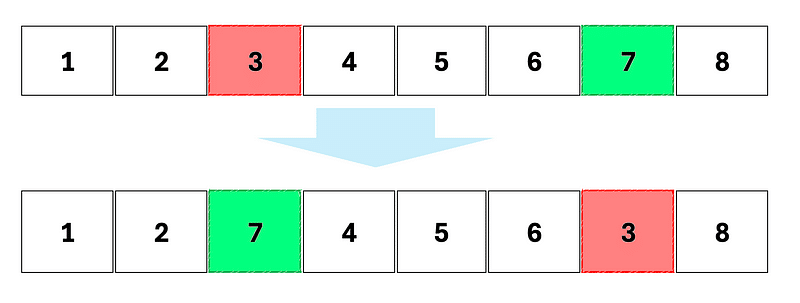
Sequence inversion: the order of part of the genome is reversed
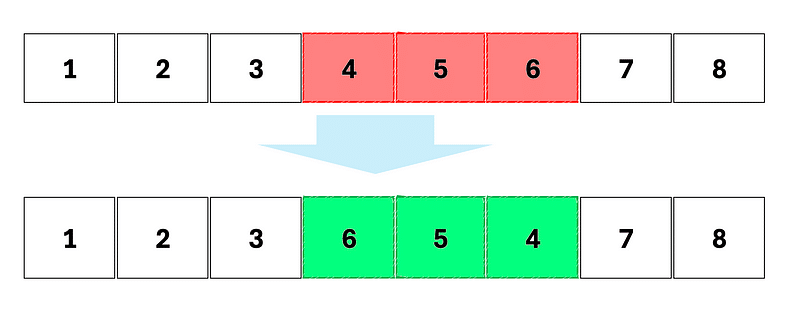
The percentage of mutations typically comprises 5% of new individuals, though I have observed mutation rates reach up to 10%. Since the elitist system tends to diminish genetic diversity, I maintained this 10% figure as a form of balance.
Iteration of the Process and Solution
By repeating the process of selecting and building new generations, we gradually produce individuals whose attributes are increasingly better suited to resolving the problem at hand.
The dilemma arises as to when the process should be halted. This depends on our constraints.
If time is limited, iterations can be stopped after a set duration. Alternatively, we might aim to attain a threshold tied to a criterion (an optimal distance for our journey, for instance, or ensuring each city visited has a minimum number of points of interest). In a trial mode, iterations can be conducted repeatedly, analyzing when iterations no longer yield significant improvement. A cap on the number of iterations can then be defined.
For this exercise, to avoid overly long computation times, I settled on 200 iterations.
Conclusion
As with many areas, nature once again proves to be a rich source of inspiration. This straightforward example illustrates how complex issues can be optimized by drawing insights from natural solutions that have evolved over hundreds of millions of years.
Ultimately, after 200 iterations, I established the following itinerary:
Glux-en-Glenne, Roussillon-en-Morvan, Alligny-en-Morvan, Anost, Quarré-les-Tombes, Saint-Léger-Vauban, Avallon, Vézelay, Bazoches, Pierre-Perthuis… totaling 154 km and incorporating 115 points of interest along the way.
By increasing the number of iterations, I could have further refined the solution, but the primary aim of this script is more educational rather than performance-driven. I aimed to avoid excessively extending the computational execution times.
For reference, utilizing Pandas dataframes isn’t optimal for performance, but again, the core objective of this script is explanatory.
You can view my complete code on my Git repo.










