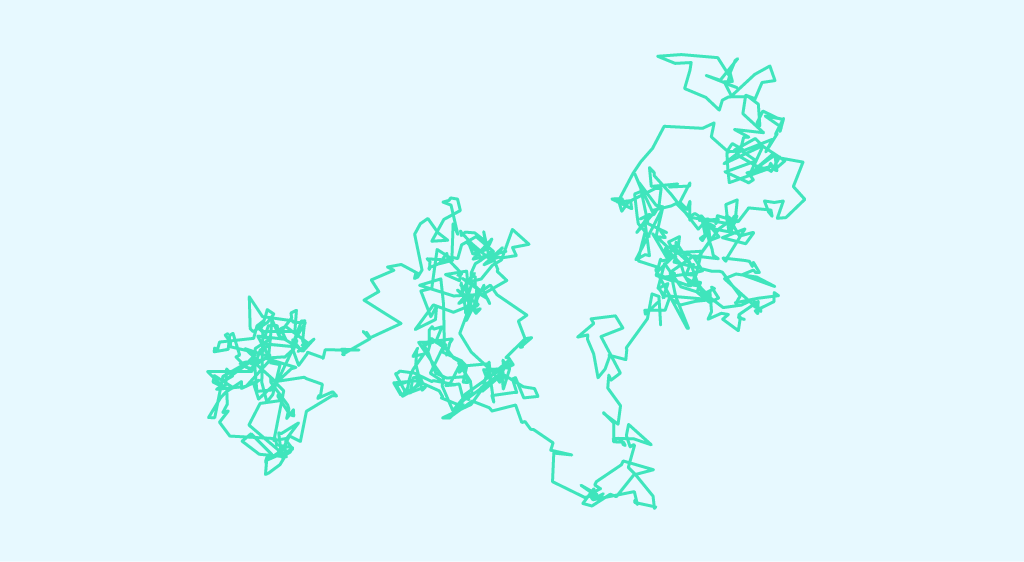
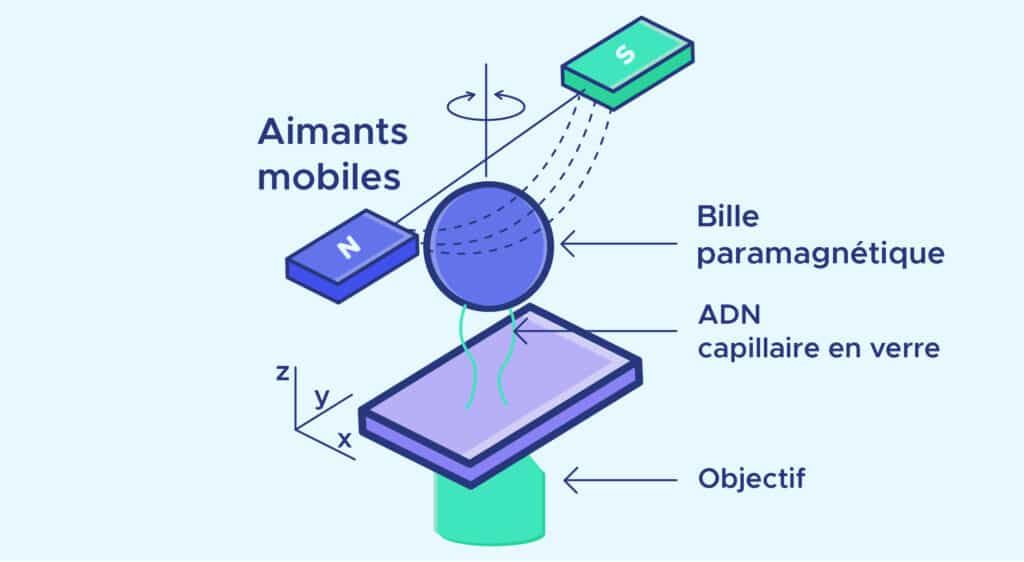
Let’s take a micrometer-sized particle immersed in a fluid. This particle will have a random motion due to the impact of other small particles on this “big” particle. This is the principle of Brownian motion, also known as the Wiener process.
Historically, it was in 1827 that botanist Robert Brown discovered Brownian motion. He observed the chaotic motion of pollen grains in water.
From 1857 onwards, Robert Brown’s work began to arouse great interest, and several scientists defined the properties of Brownian motion.
It wasn’t until Albert Einstein in 1905 that Brownian motion was described quantitatively. In particular, he related the root mean square of the distance travelled to the duration of the observation. His calculations were validated experimentally by Jean Perrin. Perrin’s experiments also led to the determination of Avogadro’s constant.
Brownian motion has applications in many fields. In physics, it is used to determine the motion of small particles such as aerosols in the air. A random force is taken into account (notably in Langevin’s equations).
Brownian motion also has mathematical applications in stochastic processes: probabilistic models that allow us to study a random phenomenon over time. This is widely used in probability, and there are several applications in finance.
The application of Brownian motion to the micromanipulation of DNA molecules
1. The principle
As an example, we’re going to look at one of the physical applications of Brownian motion, which is the micromanipulation of the DNA molecule. DNA molecules can be micromanipulated using a variety of tools, such as optical tweezers or magnetic tweezers.
The principle of micromanipulation is as follows:
- One end of the DNA molecule is attached to a glass capillary.
- A magnetic ball is attached to the other end. This ball is placed in the field of a magnet.
- By moving the magnets, the DNA molecule is pulled or rotated to create twists.
2. The benefits of Brownian motion
With this background in mind, the question arises: where does Brownian motion come into play?
The force required to stretch the DNA molecule gives some pretty important information about our macromolecule.
This force is very weak (on the order of a piconewton, i.e. 10-12 Newtons). Being weak, it is not easily measurable using conventional measuring devices, which are limited by thermal agitation.
However, Brownian motion will enable us to measure the force. Indeed, thermal agitation will create a random force that will move the ball away from its equilibrium position. Calculations show that the stretching force of the DNA molecule is directly related to the root-mean-square fluctuations.
Now we need to determine the root-mean-square fluctuations. To do this, we need to draw inspiration from Jean Perrin’s experiment.
The first step is to record the movements of the spherical particle placed at the end of the DNA molecule, using a camera connected to a microscope.
Secondly, video recognition software is used to access the coordinates of the ball at each instant. The coordinates are then used to calculate Brownian fluctuations.
3. Using Python to access the ball's coordinates
From the video, we can access the ball’s coordinates in a much more complex way, thanks to Python.
In fact, once the video has been converted into a succession of images. We use Python’s imageio library. It lets you work with images by presenting them as 3-dimensional arrays. The first two dimensions allow us to determine the position of a pixel, and the third dimension gives us information on color intensity (which will give us the color of the pixel). Once the images have been converted to grayscale, we can return to a two-dimensional array, since the values in the third dimension will all be equal (because the image is in grayscale). All we need to do is create functions that use a barycentric method to determine the coordinates of the pixel with the highest intensity. By repeating this process over the succession of images, we end up with our ball coordinates at each instant.
Access to the coordinates gives us access to the Brownian fluctuations, then to the stretching force of the DNA molecule.
In this way, Brownian motion is very useful in the micromanipulation of the DNA molecule. The work on video analysis is also a very important element. As we have seen, this process can be carried out using Python.
The training courses offered by DataScientest enable you to master Python, an indispensable tool in data science. We also offer a module on image processing: Introduction to computer vision with OpenCV.
About the author...