A model is said to possess the Markov property if its state at an instant T depends uniquely on its state at instant T-1.
If we can observe the states the model is in at each instant, we speak of an observable Markov model. Otherwise, we speak of a hidden Markov model.
In this article, we'll illustrate these models to understand how they work and how useful they are.
Observable Markov model
Consider the following situation:
You’re cooped up at home on a rainy day, and you’d like to determine the weather for the next five days.
- Since you’re not a meteorologist, you simplify the task by assuming that the weather follows a Markov model: the weather on day D depends solely on the weather on day D-1.
- To make things even simpler, you assume that there are only three possible types of weather: sunny, cloudy or rainy.
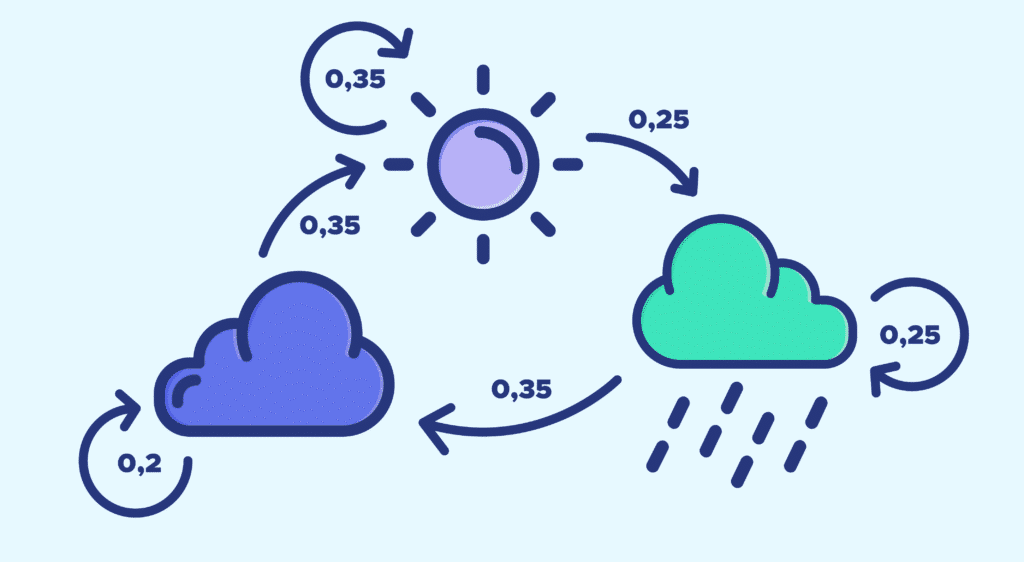
- Based on observations over the last few months, you draw up the following transition diagram:
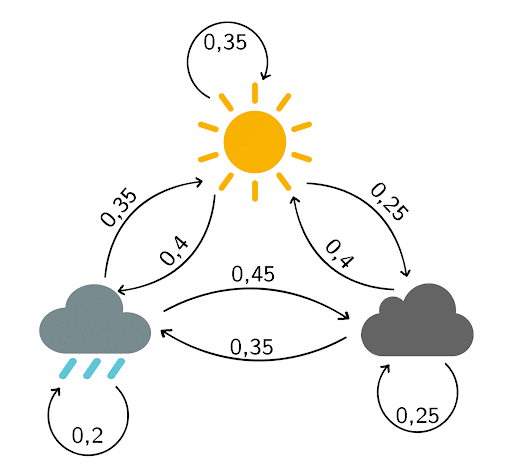
The associated transition matrix is
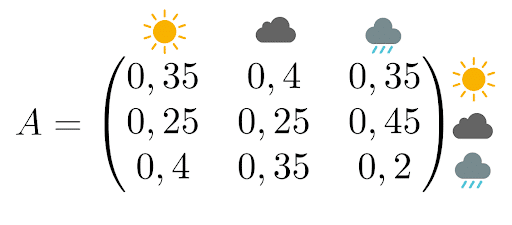
As a reminder, this matrix reads as follows:
The probability that it will be sunny tomorrow knowing that it’s raining today is 35%.
The probability that there will be clouds tomorrow knowing that there are already clouds today is 25%.
Let’s calculate the probability that the weather over the next five days will be “sunny, sunny, rainy, cloudy, sunny”.
Since the weather on any given day depends solely on the weather on the previous day, all we have to do is multiply the probabilities (as a reminder, it’s raining today):
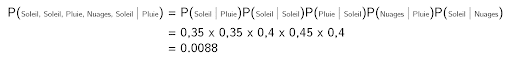
We can calculate this probability for all possible combinations, and select the combination with the highest probability to answer the problem.
In our case, here are the 5 most likely combinations:

Hidden Markov model
The same assumptions apply as in the previous section.
Now let’s suppose that a weather psychopath has locked you in a windowless room with only a computer and a lamp. Every day, the lamp lights up in a certain color according to the weather. Your kidnapper provides you with the following observation matrix:
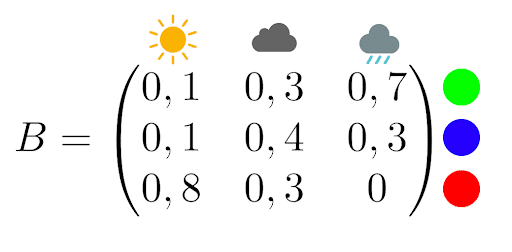
For example, if it’s raining, the lamp has a 70% chance of being green and a 30% chance of being blue.
You’ll be able to go home if you determine the weather for the next five days based solely on the color of the lamp. You then build a hidden Markov model.
You stay indoors for 5 days and find the following colors:
blue, blue, red, green, red.
You remember that it was raining the day before you were locked in.
You can then write a python code that returns the combination that has the highest probability of being realized:

NB: We could also have implemented the Viterbi algorithm, which would have returned the most likely combination, i.e. [‘Clouds’, ‘Clouds’, ‘Sun’, ‘Rain’, ‘Sun’].
This approach to prediction is interesting, but very basic. If you’d like to learn how to make more impressive predictions, using machine learning algorithms for example, contact us directly online to find out more about our data science training courses or discover other articles about machine learning:
| Image Processing |
| Deep Learning – All you need to know |
| Mushroom Recognition |
| Tensor Flow – Google’s ML |
| Dive into ML |