Das VAR-Modell: Eine umfassende Pipeline vom Geschäftsansatz bis zum Plotten der Ergebnisse
Präsentation und Dankeschön
Hallo zusammen und willkommen zu diesem Artikel, der darauf abzielt, mit Dir eine Pipeline für die Ausführung eines VAR-Modells unter Python zu entwickeln, von der Integration der Daten bis zum Plotten der Ergebnisse. Nach meiner Ausbildung in Management und Marktfinanzierung (ESCP BS) hatte ich das Vergnügen, eine Ausbildung in Data Science bei DataScientest zu absolvieren, die heute freundlicherweise diesen Artikel veröffentlichen!
Zunächst möchte ich dem Unternehmen „Les Mousquetaires“ danken, mit dem ich eine Version dieses Modells entwickeln konnte, um Vorhersagen über den Erdgasmarkt zu machen. In diesem Zusammenhang begrüße ich besonders Hélène Laroche, Leiterin des Gaseinkaufs, Quentin Pailloux, Direktor für neue Energien, Arnaud de Ligniville, Brett Chauchard & Ellias Ouidir von der Abteilung für Finanzierung und Treasury, Christelle Schneider, Virginie Hyppolite von der Abteilung für Risiken.
Für den Rest des Artikels wird jeder der folgenden Teile wie folgt aufgeteilt:
Mathematische und statistische Erklärungen unserer Entscheidungen und Beschränkungen.
Realisierung der Funktionen (verfügbar über den Git-Link).
Ausführung der Funktionen und Output
Was ist das VAR-Modell?
Das VAR-Modell für Vector Autoregression ist ein Zeitreihenmodell, das mehrere Variablen im Zeitverlauf vorhersagt. Jede der Vorhersagen jeder Variablen trägt zur Vorhersage der anderen bei. Wenn wir es also in einem linearen Format schreiben würden, würden wir Folgendes erhalten:
Es seien zwei Variablen, Y und X, und (t) ein Zeitpunkt in der Zeit.
Y(t+1) = f(Y(t), X(t))
X(t+1) = f(X(t), Y(t))
Y(t+1) = α1 + β1Y(t) + β2X(t) + ε1
X(t+1) = α2 + β3X(t) + β4Y(t) + ε2.
Mit α als Konstanten, β als den Variablen zugeordneten Koeffizienten, ε als Fehler.
Das Modell berechnet auf der Grundlage der Historie die Konstanten, Koeffizienten für jede Variable.
Außerdem enthält das Modell „Lags“ (λ), die es ermöglichen, in die Berechnung von X(t+1), Y(t+1) alle Werte von X, Y bis zu X(t- λ), Y(t- λ) einzubeziehen.
Hier findet sich die Erklärung für den Namen wieder: Ein selbstregulierender Vektor.
Welchen Nutzen hat das VAR-Modell?
Das VAR-Modell kann sehr interessant sein, um mit maschinellen Lernmodellen wie dem RandomForestRegressor oder dem XGBoostRegressor zu konkurrieren, wenn deine Variable eine Zeitreihe ist. Die Grundlagen seiner Literatur sind solide, obwohl einige Aspekte noch diskutiert werden (wir kommen später darauf zurück).
Der Vorteil dieses Modells ist, dass es den Berufen sehr leicht erklärt werden kann, da es auf statistischen Grundlagen beruht, die leicht zu erklären und zu verstehen sind.
Das VAR-Modell kann verwendet werden, um eine Reihe von Variablen vorherzusagen, aber man kann es auch verwenden, um sich auf eine einzige Variable zu konzentrieren, was hier unser Fall ist.
Definition des Problems und des Vorhersagefensters
Bevor wir etwas vorhersagen können, brauchen wir ein Problem – und Variablen!
Es ist mir nicht möglich, mein Dataset zu enthüllen, aber ich werde dich in die Methodik der Variablenauswahl einführen, damit du sie in allen Fällen anwenden kannst.
Angenommen, dein Beruf verlangt von dir ein Modell, mit dem du eine Zahl vorhersagen kannst (Regressionstyp in der Datenwissenschaft).
-> Ist diese Variable abhängig oder wird sie im Laufe der Zeit beobachtet?
bh
-> Ist diese Variable von vornherein mit anderen Variablen verknüpft?
mp,g
-> Sind diese anderen Variablen auch im Laufe der Zeit beobachtbar?
Wenn du diese drei Fragen mit Ja beantwortet hast, dann könnte das VAR-Modell deinem Bedarf entsprechen.
Wie wählt man das Vorhersagefenster?
Dies ist eine knifflige, aber sehr interessante Frage: Wie viele Tage soll (und kann!) ich vorhersagen? Die Branche hat vielleicht einen konkreten Bedarf, z. B. 30 Tage, 120 Tage, 360 Tage… Aber vielleicht hast Du nicht die nötige Menge an Daten?
Ich empfehle Dir, mit dem Bedarf der Branche zu beginnen und dann das Tempo zu drosseln, wenn Du mit statistischen Tests nicht so weit kommst. Umgekehrt, wenn alles für den Zeitraum funktioniert, den dein Geschäft von dir verlangt, warum nicht weiter in die Zukunft gehen? Im Allgemeinen kann ich nur empfehlen, deine Pipeline auf verschiedenen Zeitzielen zu testen.
Die erklärenden Variablen :
Versuche erstens, so viele Variablen wie möglich zu identifizieren, die deine Zielvariable beeinflussen könnten.
Je mehr Variablen du hast, desto wahrscheinlicher ist es, dass du diejenigen entdeckst, die deine Zielvariable beeinflussen. Wir argumentieren hier im Design-Thinking-Modus: Qualität durch Quantität. Keine Sorge, wir werden dann die interessantesten Variablen auswählen, um sie in das endgültige Modell aufzunehmen.
Achte darauf, dass deine Daten die gleiche Zeiteinheit haben: Wenn deine Zielvariable in Tageseinheiten ausgedrückt ist, achte darauf, dass der Rest auch in Tageseinheiten ausgedrückt ist!
Die Verwaltung von NaN
Wenn dein Datensatz einige Lücken aufweist, kannst Du natürlich auf die fillna()-Methoden von Python zurückgreifen. Für einen vielleicht solideren Ansatz, insbesondere wenn die Anzahl der NaNs zu groß wird, empfehle ich Dir etwas Lektüre und das MICE-Modell.
Für den Fall, dass Du über einen längeren Zeitraum Daten über bestimmte Reihen hast, über andere aber nicht, empfehle ich Dir, darüber nachzudenken, sie entweder ganz zu droppen oder Deinen Datensatz so zu kürzen, dass Du in deiner ersten Zeile alle Deine Variablen vollständig hast.
Hier sind einige Funktionen, um die Daten in einen einzigen Dataframe zu integrieren: def agreg_df (siehe den GIT-Link).
Und eine Funktion zum Ersetzen: def replace_na (siehe GIT-Link).
Und dann führen wir den Code aus:
Statistischer Bedarf und geeignete Umwandlungen
Unsere Zeitreihen müssen ein grundlegendes Kriterium erfüllen: die Stationarität.
Unabhängig vom Zeitpunkt (t) in der Zeit ist der Erwartungswert unserer Variable immer derselbe. Es gibt keinen Trend und ihre Varianz ist immer gleich und nicht unendlich, und die Autokorrelation zwischen zwei Zeitpunkten hängt nur von der zeitlichen Verschiebung ab.
Ich empfehle diesen Feed auf researchgate für weitere Details über die Notwendigkeit der Stationarität.
Nun, da das Problem gestellt ist, was tun wir?
Transformation mithilfe von Box-Cox
Es kann sehr nützlich sein, unsere Daten zu transformieren, bevor wir ihre Stationarität testen. Transformationen haben viele Vorteile, wie z. B. das Entfernen (oder Verringern) des saisonalen Aspekts, des Trends. Eine sehr praktische Transformation ist die Box-Cox-Transformation: Abhängig von einem bestimmten Lambda-Parameter zwischen [-1 ;1] wird die Serie auf unterschiedliche Weise transformiert, hier die Dokumentation der Funktion in Python.
Was uns besonders interessieren wird, ist das Lambda-Argument und sein Wert „None“: In diesem Fall wählt die Funktion selbstständig den optimalen Parameter aus! In diesem Fall ist das zweite Element, das die Funktion zurückgibt, das „Lambda“, das mit der transformierten Reihe verknüpft ist.
Der Stationaritätstest und die Differenzierung
Mit dem erweiterten Dickey-Fuller-Test kann die Stationarität einer Zeitreihe getestet werden.
Die Hypothese H0 des Tests lautet: „Die Daten weisen eine Einheitswurzel auf, die Reihe ist also nicht stationär“.
Wir werden uns also darauf konzentrieren, diese Hypothese mit einem Vertrauensniveau von 95% abzulehnen. Das bedeutet, dass der Test einen p-Wert von weniger als 0,05 zurückgeben muss. Hier ist die Dokumentation der Funktion.
Ich schlage dir die folgende Funktion für eine Formatierung des Tests vor
def dickey_fuller_test (siehe GIT-Link).
Für den Fall, dass mindestens eine der Variablen nicht stationär ist, werden wir eine Differenzierung vornehmen:
Data_diff(t) = observation(t) – observation(t-1).
Mit (t) einem Zeitpunkt in der Zeit.
Differenzieren ist eine Form der Transformation, und sie funktioniert sehr gut, um zur Stationarität von Reihen zu gelangen.
Es gibt eine Pandas-Methode auf Dataframes, um zu differenzieren: df.diff()
Für den Fall, dass eine erste Differenzierung nicht ausreicht, um Stationarität in unseren Reihen zu erreichen, können wir ein zweites Mal differenzieren. Wenn das immer noch nicht ausreicht, ist es besser, die Variable aufzugeben oder nach anderen Methoden zur Stationarisierung zu suchen.
Kommen wir nun zur Ausführung des Codes für diesen Teil!
Es kann sein, dass du „0“ in deinen Daten hast: Dann musst du dem gesamten DF eine „1“ hinzufügen, damit die Transformation funktioniert:
Problem: Alle Variablen sind nicht-stationär…
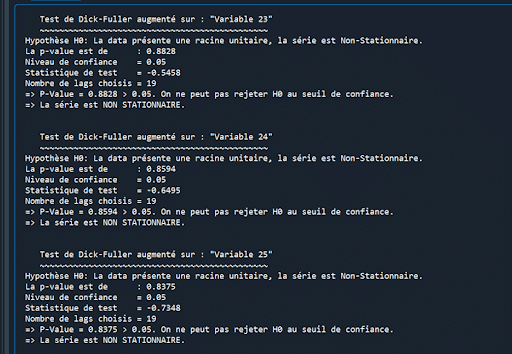
Dieses Mal ist alles in Ordnung! Meine Reihen sind stationär.
JEDOCH, Achtung: Es ist zu beachten, dass eine zweite Differenzierung dazu führt, dass unsere Variablen Informationen verlieren.
Wenn also nach einer ersten Differenzierung nicht alle deine Reihen stationär sind, musst du zwei Familien von Modellen optimieren und vergleichen:
Eine erste Familie auf den EINMAL differenzierten Daten, OHNE die nicht-stationären Variablen.
Eine zweite Familie auf den ZWEIMAL differenzierten Daten, MIT den Variablen, die stationär geworden sind.
In meinem Fall weiß ich, dass das zweimal differenzierte Modell im Vergleich zum Hinzufügen der beiden neuen stationären Variablen zu viel Signal verliert. Ich werde also mit den einmal differenzierten Daten arbeiten, ohne die beiden Variablen, die nicht differenziert sind. Wir werden sie also droppen, dann den Zug erstellen und test set
Auswahl der Variablen und des Maxlags: Iteration durch den Granger-Test
Nicht alle Variablen, die wir ausgewählt haben, sind für unser Modell geeignet. Die Frage, die wir uns stellen müssen, lautet: Beteiligen sich alle Variablen effektiv an der Vorhersage der anderen, insbesondere der Zielvariablen?
Es gibt einen Test, der diese Frage beantworten kann: der Granger-Test. Mit ihm wird getestet, ob die Vorhersagen der Variablen X die Vorhersagen der Variablen Y signifikant beeinflussen. Die HO-Hypothese des Tests lautet: „Die Vorhersagen der Variable X beeinflussen die Vorhersagen der Variable Y nicht“. Wir wollen also, bei einem Konfidenzniveau von 95%, p-Werte unter 0,05. Die Wikipedia-Seite des Tests erklärt dies aus meiner Sicht sehr gut. Und hier ist die Dokumentation des Tests unter Python.
Was hier besonders interessant ist und beachtet werden sollte, ist das Argument „maxlag“: Es wird bestimmen, wie viele Lags unser Test maximal in Anspruch nehmen wird. Und hier werden wir iterative Tests durchführen müssen, da maxlag die p-Werte verändert, und zwar potenziell drastisch: Variablen, die den Test bei maxlag = 10 nicht bestehen, können ihn bei maxlag 20 vollständig bestehen.
Ich schlage den folgenden Code für eine Funktion des grangers test vor:
def grangers_test (siehe GIT-Link).
Wie lesen wir den DF, der an uns zurückgegeben wird?
Die Variablen in der Spalte (die X) sind diejenigen, deren Vorhersagegewicht auf die Vorhersagen der Y-Variablen getestet wird (wir werden uns weiter unten ein Beispiel ansehen). Wenn der Wert kleiner als 0,05 ist, dann wird tatsächlich H0 verworfen und somit beeinflussen die Vorhersagen von X die Vorhersagen von Y.
Unser Ziel ist es, eine Tabelle zu haben, in der alle Werte (außer der Diagonale) kleiner als 0,05 sind: Das bedeutet, dass alle Variablenpaare die Hypothese H0 ablehnen.
Aber bevor wir unsere Variablen mit dieser Funktion testen, müssen wir den Maxlag bestimmen.
Dazu werden wir unser VAR-Modell mit einem zufällig ausgewählten Maxlag trainieren. Wenn das Training funktioniert, erhöhen wir den Maxlag, bis der Code abstürzt: Ein zu hoher Maxlag führt zu einem Problem mit den Gleichungen. Wenn wir den Maxlag bestimmt haben, gehen wir zur Auswahl der Variablen über.
Dazu gehen wir in Iterationen wie folgt vor:
Wir testen mit unserer Funktion und dem Maxlag und zeigen den DF an.
Wir schauen uns die Spalte ODER die Zeile an, die die meisten Werte >0,05 enthält. Im Fall der Spalten bedeutet dies: Meine Variable X bestimmt zu wenig von Y. Im Fall von Zeilen: Meine Variable Y wird zu wenig von X bestimmt. Wenn wir eine Variable finden, die sowohl in der Zeile als auch in der Spalte viele 0,05-Werte enthält, ist das perfekt, da wir dann eine Variable, die die anderen Variablen nur wenig erklärt und wenig erklärt, auf einen Schlag entfernen.
Wir entfernen die ausgewählte Variable aus unserem aktuellen DF, aber auch aus dem Basis-DF, da wir ihn später für die Rücktransformationen verwenden werden, brauchen wir die gleichen Spalten.
Wir trainieren unser Modell, um den neuen „Maxlag“ zu finden, der das Modell nicht zum Absturz bringt.
Wir kehren zu Schritt 1 zurück, bis der DF nur noch Werte <0,05 enthält.
Hier ist der Code, der mit dieser Passage verbunden ist, mit einigen Iterationen und Screenshots zur Veranschaulichung :
Hier ist ein Screenshot von dem, was ich erhalte (Achtung, dieser Vorgang ist der längste in unserer Modellierung).
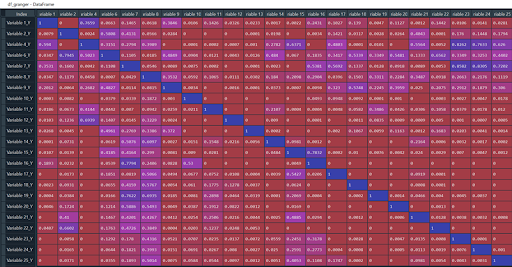
Zur Erinnerung: Unsere Variable 1 ist die Zielvariable des Projekts, wir müssen sie behalten.
Auf einen Blick denke ich, dass die Variable 8 ein guter Kandidat ist: Hier ist die Anzahl der p-Werte >0,05 am größten.
Wir droppen sie, ändern die Sets :
Wir suchen nach einem neuen optimalen Maxlag (so hoch wie möglich), indem wir den vorherigen Codeblock erneut ausführen (maxlag, model_var, res).
In meinem Fall steigt er auf 19. Ich führe den Granger-Test erneut durch:
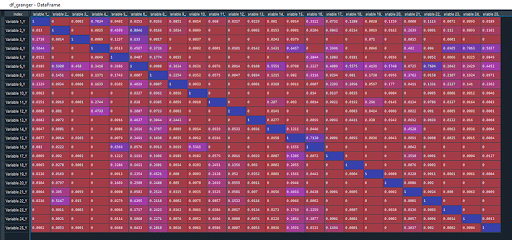
Jetzt ist es die Variable 6, die der beste Kandidat ist.
Ich werde sie droppen und die vorherigen Schritte wiederholen, bis der DF so aussieht (kein p-Wert >0,05):
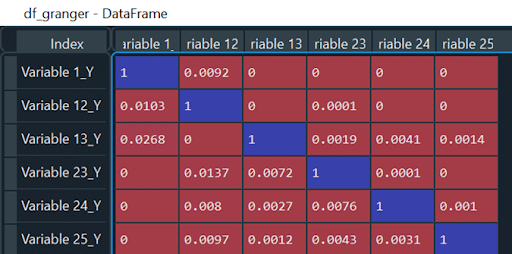
Iteriere durch den Maxlag, um das beste Modell zu finden.
Nachdem wir den df_granger bereinigt haben, holen wir uns unseren höchsten maxlag (also den letzten). In meinem Fall ist maxlag = 67.
Wir werden eine Vorlage pro maxlag erstellen und jedes Mal die folgenden Elemente abrufen:
Den MAE (oder deine Zielmetrik), den p-Wert des Tests auf Normalität der Residuen, den p-Wert des Tests auf Weiße der Residuen.
Einige Spezifikationen zur Normalität und Weiße:
Residuen, die den Test auf Normalität bestehen, bedeuten, dass die Fehler einer Normalverteilung folgen. Dies ist eine notwendige Bedingung, um die klassischen Konfidenzintervalle zu erstellen. Falls die Residuen den Test nicht bestehen, müssen wir mit Bootstraping arbeiten, was das Thema eines zukünftigen Artikels sein wird!
Ein erfolgreicher Test auf Weiße der Residuen bedeutet, dass die Residuen die Form von weißem Rauschen haben, was bedeutet, dass aus unseren Variablen keine Informationen mehr (oder nur noch am Rande) zu gewinnen sind. Man kann ein Modell, das den Test auf weiße Residuen nicht besteht, immer noch verbessern, aber nur weil ein Modell den Test besteht, bedeutet das nicht, dass es nicht verbesserungswürdig ist!
Man kann ein Modell leicht verbessern, indem man zu allen Vorhersagen den Mittelwert der Verzerrungen hinzufügt, was in unserer Pipeline geschieht.
Die vorherigen Punkte sind fast eine Paraphrase der ausgezeichneten Arbeit von Rob J Hyndman und George Athanasopoulos in „Forecasting, principles and practice“, die du hier kostenlos finden kannst und die ich dir wärmstens empfehlen kann: https://otexts.com/fpp2/.
Ich schlage dir folgende Funktion für unsere konkrete Pipeline vor:
def pipeline_var (siehe GIT-Link).
Die Aufmerksameren unter euch werden bemerkt haben, dass wir die Funktion „inv_diff“ innerhalb von „pipeline_var“ verwenden, die auch im git verfügbar ist. Achte auf den Parameter „second_diff“! False, wenn wir einmalig differenzierte Daten verwenden, True andernfalls.
Jetzt führen wir das Ganze aus und speichern unsere MAEs und p-Werte aus den Tests. Ich drucke „i“, um die Ausführung zu verfolgen. Vergiss nicht, im Fitting des Modells verschiedene Werte für die Parameter „ic“ und „trend“ zu testen!
Nachdem wir den df_granger bereinigt haben, holen wir uns unseren höchsten maxlag (also den letzten). In meinem Fall ist maxlag = 67.
Wir werden eine Vorlage pro maxlag erstellen und jedes Mal die folgenden Elemente abrufen:
Den MAE (oder deine Zielmetrik), den p-Wert des Tests auf Normalität der Residuen, den p-Wert des Tests auf Weiße der Residuen.
Einige Spezifikationen zur Normalität und Weiße:
Residuen, die den Test auf Normalität bestehen, bedeuten, dass die Fehler einer Normalverteilung folgen. Dies ist eine notwendige Bedingung, um die klassischen Konfidenzintervalle zu erstellen. Falls die Residuen den Test nicht bestehen, müssen wir mit Bootstraping arbeiten, was das Thema eines zukünftigen Artikels sein wird!
Ein erfolgreicher Test auf Weiße der Residuen bedeutet, dass die Residuen die Form von weißem Rauschen haben, was bedeutet, dass aus unseren Variablen keine Informationen mehr (oder nur noch am Rande) zu gewinnen sind. Man kann ein Modell, das den Test auf weiße Residuen nicht besteht, immer noch verbessern, aber nur weil ein Modell den Test besteht, bedeutet das nicht, dass es nicht verbesserungswürdig ist!
Man kann ein Modell leicht verbessern, indem man zu allen Vorhersagen den Mittelwert der Verzerrungen hinzufügt, was in unserer Pipeline geschieht.
Die vorherigen Punkte sind fast eine Paraphrase der ausgezeichneten Arbeit von Rob J Hyndman und George Athanasopoulos in „Forecasting, principles and practice“, die du hier kostenlos finden kannst und die ich dir wärmstens empfehlen kann: https://otexts.com/fpp2/.
Ich schlage dir folgende Funktion für unsere konkrete Pipeline vor:
def pipeline_var (siehe GIT-Link).
Die Aufmerksameren unter euch werden bemerkt haben, dass wir die Funktion „inv_diff“ innerhalb von „pipeline_var“ verwenden, die auch im git verfügbar ist. Achte auf den Parameter „second_diff“! False, wenn wir einmalig differenzierte Daten verwenden, True andernfalls.
Jetzt führen wir das Ganze aus und speichern unsere MAEs und p-Werte aus den Tests. Ich drucke „i“, um die Ausführung zu verfolgen. Vergiss nicht, im Fitting des Modells verschiedene Werte für die Parameter „ic“ und „trend“ zu testen!
Überprüfung des Granger-Tests für den neuen optimalen Lag
Da mein bester MAE bei einem maxlag von weniger als 67 erzielt wurde, d.h. dem höchsten lag, mit dem ich meine Granger-Tests durchgeführt habe, muss ich meine Granger-Matrix mit einem lag von 44 erneut testen. Wir werden also unsere df mit maxlag = 44 erneut testen, und ich erhalte folgendes Ergebnis:
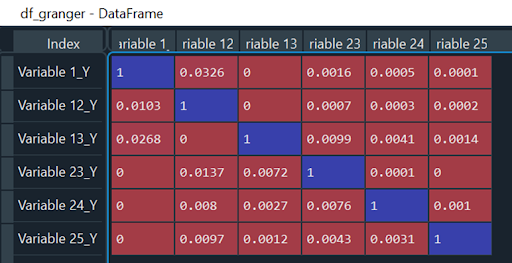
Da keiner meiner P-Werte den Test versagt, kann ich beruhigt schlussfolgern, dass mein bestes Modell mit lag = 44 erzielt wird.
Ergebnisse, Grafiken, Metriken
Ich schlage Dir die folgenden zwei Funktionen vor, um deine Vorhersagen gegen die Realität zu plotten:
def plot_pred_true
def plot_pred_true_total
Wir trainieren das beste Modell und zeigen die Grafiken an:
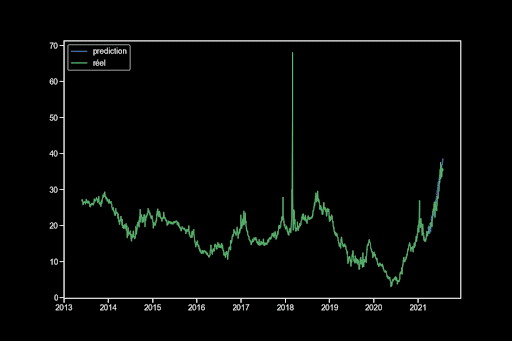
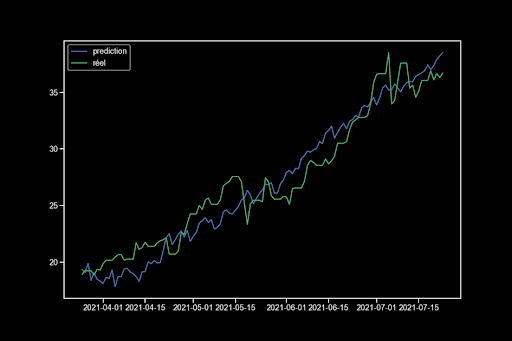
Ich erhalte also über 120 Tage eine Vorhersage mit einem MAE von 1,44. Mein Weißheitstest besteht nicht, was bedeutet, dass es noch Informationen in meinen Variablen gibt. Der Normalitätstest besteht ebenfalls nicht, sodass ich die klassischen Konfidenzintervalle nicht verwenden kann.
Vielen Dank, dass du mich bis hierher gelesen hast! Ich hoffe, dass dieser Artikel dir helfen kann. Bitte kommentiere oder kontaktiere mich bei Fragen!
Wenn Du, genau wie Victor, gerne lernen möchtest, wie man mit Daten umgeht, dann sind wir für Dich da!









