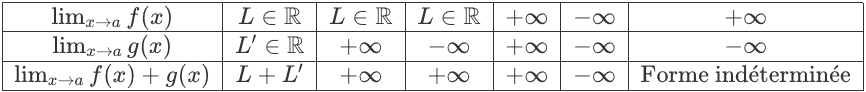Alle wissenschaftlichen Disziplinen basieren auf Mathematik, und die Datenwissenschaft ist da keine Ausnahme. Wenn es sich bei den zu lösenden Problemen um Optimierungsprobleme handelt, ist es notwendig, zu wissen, was der Grenzwert einer Funktion ist. In diesem Artikel erfährst du, wie du den Grenzwert einer Funktion bestimmen kannst.
Grenzwert einer Funktion vs. Grenze: Definition
Der Grenzwert einer Funktion f ist der Wert, dem sich die Funktion annähert, wenn ihr Argument sich einem bestimmten Wert annähert.
Mathematisch schreibt man
\lim \limits_{x \to a} f(x) = l
Man sagt, dass f gegen l strebt, wenn x gegen a strebt.
Je nach Fall können a und l reelle Zahlen sein oder gleich \pm \infty.
Grenzwerte gebräuchlicher Funktionen
- Endliche Grenzen in einem reellen Wert
Zum Beispiel ist für f(x) = x^2 der Grenzwert, wenn x gegen 2 tendiert, 2^2 = 4.
- Grenzen zur Unendlichkeit
Wenn die Funktion in einer reellen Zahl a gut definiert ist (man sagt, sie ist stetig in a), dann ist der Grenzwert in a genau f(a).
Wenn die Variable x sehr große Werte annimmt (positiv oder negativ), sagt man, dass x mehr oder weniger gegen unendlich strebt. In diesem Fall unterscheidet man zwischen Fällen, in denen f(x) sich einem endlichen Wert nähert, und Fällen, in denen f(x) sich gegen unendlich bewegt. Im ersten Fall sagt man, dass f konvergiert, und im zweiten Fall, dass f divergiert.
Unten findest du eine Tabelle, die die Grenzen üblicher Funktionen im Unendlichen zusammenfasst.
\begin{array}{|c|c|c|}
\hline \text{Funktion} & \text{grenzt an }+ \infty, \: x \to +\infty & \text{grenzt an }-\infty ,\:x \to - \infty \\
\hline f(x) = x & +\infty & -\infty \\
\hline f(x) = x^n \quad n \geq 1 & +\infty & \begin{cases} & + \infty \text{ si } n \text{ ist gerade } \\ & - \infty \text{ si } n \text{ ist ungerade} \end{cases} \\
\hline f(x) = e^x & +\infty & 0 \\
\hline f(x) = \sqrt{x} & +\infty & \text{nicht definiert} \\
\hline f(x) = \frac{1}{x} & 0 & 0 \\
\hline f(x) = \ln(x) & +\infty & \text{nicht definiert} \\
\hline
\end{array}
Wenn eine Funktion einen endlichen Grenzwert l \in \mathbb{R} hat, wenn x \to \infty, dann sagt man, dass f eine horizontale Asymptote mit der Gleichung y = l hat. Das heißt, die Kurve nähert sich immer mehr der Geraden y=l.
- Limites infinies en une valeur finie
\begin{array}{|c|c|}
\hline \text{Funktion} & \text{grenzt an } 0, \: x \to 0 \\
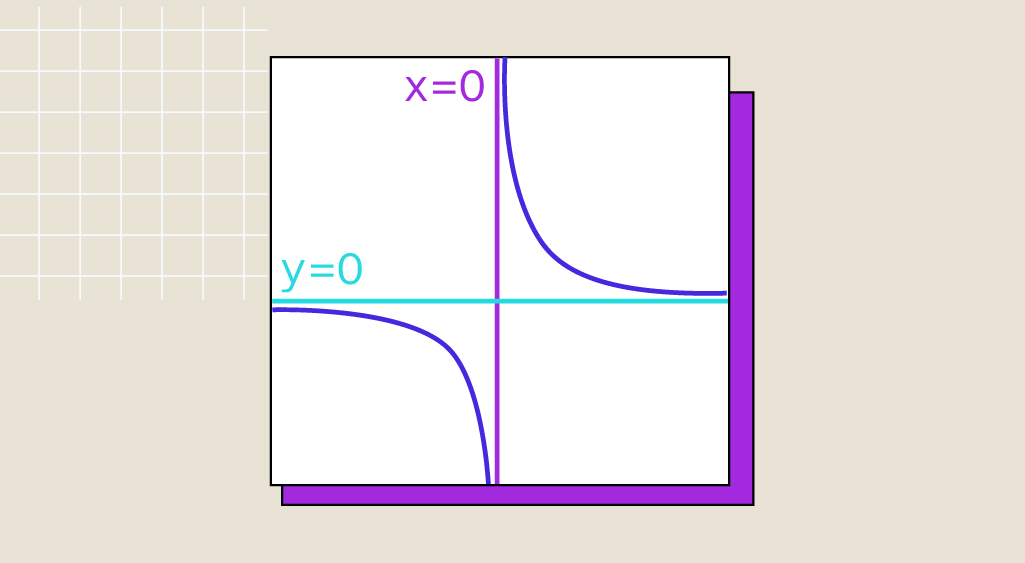
\hline f(x) = \frac{1}{x} & \begin{cases} & +\infty \text{ si } x \gt 0 \\ & \infty \text{ si } x \lt 0 \end{cases} \\
\hline nan & nan \\
\hline f(x) = \ln(x) & -\infty \\
\hline f(x) = \sqrt{x} & 0 \\
\hline
\end{array}
Wenn lim_{x \to a} f(x) = \pm \infty, wobei a eine reelle Zahl ist, dann sagt man, dass die Kurve von f eine vertikale Asymptote in a hat. Das heißt, die Kurve nähert sich immer mehr der Geraden mit der Gleichung x=a.
Limit-Operationen
In den meisten Fällen ist es möglich, Limitoperationen durchzuführen, um das Limit zu bestimmen.
Grenzwert einer Summe von zwei Funktionen
Grenzwert eines Produkts aus zwei Funktionen
Grenzwert eines Quotienten aus zwei Funktionen
Klicke auf die Tabellen, um sie im Vollbildmodus anzuzeigen.
Einen Grenzwert praktisch bestimmen
Um Grenzwerte zu bestimmen, ist es manchmal einfacher, andere Funktionen zu verwenden.
Das Vergleichen von Funktionen ermöglicht es, ihre Grenzwerte zu vergleichen, sofern sie existieren.
Das Vergleichen von Funktionen ermöglicht es, ihre Grenzwerte zu vergleichen, sofern sie existieren.
Es gibt zwei Haupteigenschaften beim Vergleich von Funktionen
- Vergleichstheorem
Es seien f und g zwei Funktionen, die auf einem Intervall I = [a, +infty[ definiert sind.
. Es wird angenommen, dass für jedes x \in I \; f(x) \geq g(x).
. Es wird angenommen, dass für jedes x \in I \; f(x) \geq g(x).
Wenn \lim_{x \to +\infty}g(x) = +\infty, dann \lim_{x \to +\infty}f(x) = +\infty
Wenn \lim_{x \to +\infty}f(x) = -\infty, dann \lim_{x \to +\infty}g(x) = -\infty
- Gendarmen-Theorem
Es seien f, g und h drei Funktionen, die auf einem Intervall I = [a, +infty[] definiert sind.
. Es wird angenommen, dass für jedes x \in I \; g(x) \leq f(x) \leq h(x).
. Es wird angenommen, dass für jedes x \in I \; g(x) \leq f(x) \leq h(x).
Wenn g und h gegen denselben Grenzwert l in +infty streben, dann ist \lim_{x\to +infty}g(x) = +infty.
Du weißt nun, was ein Grenzwert ist und wie man ihn berechnet. Durch die Berechnung von Grenzen kann z. B. die Ableitung einer Funktion als Grenze einer Steigerungsrate definiert werden.
Mehr dazu findest du in unserem Artikel über die Ableitung einer Funktion.
Wenn du alle mathematischen Konzepte, die in der Datenwissenschaft eine Rolle spielen, kennenlernen möchtest, laden wir dich ein, unsere Weiterbildungen zu entdecken.
Wenn du alle mathematischen Konzepte, die in der Datenwissenschaft eine Rolle spielen, kennenlernen möchtest, laden wir dich ein, unsere Weiterbildungen zu entdecken.