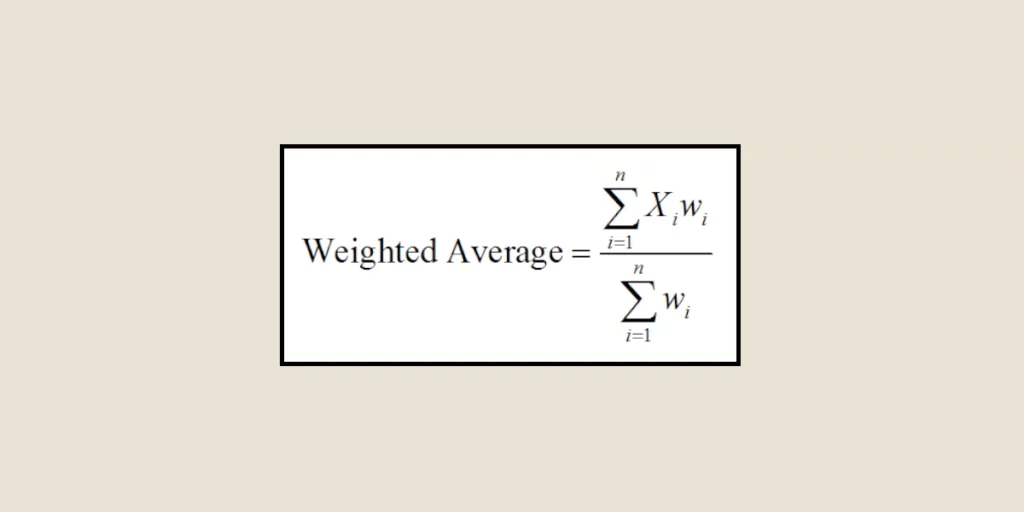Die Berechnung eines einfachen Durchschnitts kann in Analysezusammenhängen irreführend sein. Durch die Gewichtung bestimmter Zahlen innerhalb einer Liste kann eine viel präzisere Wahrnehmung erzielt werden.
Nicht alle Informationen haben die gleiche Bedeutung, und eine fundierte Analyse eines beliebigen Sektors muss diesen Faktor berücksichtigen. Wenn man sich lediglich auf einfache Formeln wie den Durchschnitt einer Zahlenreihe verlässt, trifft man häufig unzureichende Entscheidungen.
Lassen wir uns das mit einem einfachen Beispiel verdeutlichen. Ein Lehrer entscheidet am Ende des Jahres darüber, ob Schüler in die nächste Klasse aufsteigen dürfen, basierend auf dem folgenden Kriterium: Der Notendurchschnitt muss über 10 liegen. Hier ist eine vereinfachte Tabelle mit den Noten mehrerer Schüler.
| Joey | Monica | Rachel | |
|---|---|---|---|
| Test 1 | 12 | 7 | 11 |
| Prüfung Trimester | 9 | 12 | 12 |
| Test 2 | 14 | 6 | 10 |
| Jahresabschlussprüfung | 8 | 14 | 11 |
| Durchschnitt | 10,75 | 9,75 | 11 |
Wir haben hier drei Schüler: Joey, Monica und Rachel. Jeder von ihnen hat vier Prüfungen zur Wissensüberprüfung absolviert: Test 1, Prüfung Trimester, Test 2 und so weiter.
Wenden wir den Durchschnitt auf diese Noten an, zeigt sich, dass zwei Schüler genügend Punkte haben, um in die nächste Klasse aufzusteigen: Joey und Rachel. Monica hingegen fällt durch.
Das Prinzip des gewichteten Durchschnitts
Bei der Berechnung des gewichteten Durchschnitts berücksichtigen wir einen wichtigen Faktor: Nicht jede Prüfung besitzt die gleiche Bedeutung. Zum Beispiel hat die Prüfung Trimester doppelt so viel Gewicht wie die Tests. Die Jahresabschlussprüfung hat viermal so viel Gewicht wie ein einfacher Test, da sie alle während des Jahres behandelten Themen abdeckt.
Der gewichtete Durchschnitt bezieht diesen Faktor ein, indem er jeder Prüfung ein bestimmtes Gewicht zuweist. So haben die Tests einen Koeffizienten von 1, die Prüfung Trimester einen Koeffizienten von 2, und die Jahresabschlussprüfung einen Koeffizienten von 4.
Der gewichtete Durchschnitt wird dann wie folgt berechnet:
(Note x Koeffizient) + (Note x Koeffizient) + (…) / Summe der Koeffizienten
| coefficient | Joey | Monica | Rachel | |
|---|---|---|---|---|
| Test 1 | 1 | 12 | 7 | 11 |
| Prüfung Trimester | 2 | 18 | 24 | 24 |
| Test 2 | 1 | 14 | 6 | 10 |
| Jahresabschlussprüfung | 4 | 32 | 56 | 44 |
| Gewichteter Durchschnitt | 9,5 | 11,63 | 11,13 |
Zum Beispiel wird der gewichtete Durchschnitt von Joey wie folgt berechnet: (12 x 1) + (9 x 2) + (14 x 1) + (8 x 4) / 8. Und was sehen wir, wenn wir diese Rechnung durchführen? Eine völlig andere Situation. Jetzt erscheint Monica als die beste Schülerin und besteht mit Bravour. Joey hingegen fällt durch!
Vorteile des gewichteten Durchschnitts
Wie Du im obigen Beispiel siehst, bietet der gewichtete Durchschnitt ein viel genaueres Bild des Leistungsniveaus jedes Schülers. Damit haben wir ein Werkzeug, das den Weg zu fundierten Entscheidungen ebnet.
Nehmen wir nun den Fall eines Online-Shops, der Kundenbewertungen sammelt. Sie haben ein Warnsystem eingerichtet: Wenn der Notendurchschnitt einer Woche unter 3 von 5 liegt, müssen sofort Korrekturmaßnahmen ergriffen werden. Aber … Stell Dir vor, in der Gruppe gibt es 5 spezielle Kunden, die allein 60 % des Umsatzes ausmachen. Da ihre Meinung entscheidend ist, wäre es sinnvoll, ihren Bewertungen ein viel größeres Gewicht zu geben als denen von Gelegenheitskäufern. So könnte der gewichtete Durchschnitt ein Phänomen aufdecken, das normalerweise unbemerkt bleiben könnte.
Gewichtung eines Wertpapierportfolios
Dieses Prinzip des gewichteten Durchschnitts ist so bedeutend, dass es auch bei der Berechnung der Kapitalgewinne eine Rolle spielt, die ein Investor nach dem Verkauf von Aktien an den Fiskus melden muss. Auch hier wird ein Beispiel verdeutlichen, warum dies der Fall ist.
Angenommen, ein Investor erwirbt:
- 100 Aktien à 20 € von einem Startup im ersten Jahr
- 200 Aktien à 50 € des gleichen Startups im folgenden Jahr.
Wenn der Investor sich mit einem „klassischen“ Durchschnitt begnügt, indem er berücksichtigt, was er ausgegeben hat, erhält er einen Durchschnitt von 35 €. Diese Zahl ist jedoch irreführend, da sie den gezahlten Beträgen (20 und 50 €) die gleiche Bedeutung beimisst. Wenn er seine Aktien zum Preis von 38 € verkaufte, könnte der Investor den Eindruck haben, einen Gewinn erzielt zu haben. In Wahrheit ist das nicht der Fall.
Um den gewichteten Durchschnitt zu erhalten, multiplizieren wir die 100 Aktien mit 20 € im ersten Jahr und die 200 Aktien mit 50 € im zweiten Jahr, also 2.000 + 10.000 und somit insgesamt 12.000 Euro. Dieser Gesamtbetrag wird dann durch die Anzahl der in diesem Zeitraum erworbenen Aktien (300) geteilt. Wir erhalten dann einen gewichteten Durchschnitt von 40 €. Daraus ergibt sich, dass ein Verkauf zu 38 € einem Verlust entsprechen würde.
Eine Hilfe bei der Entscheidungsfindung
Der gewichtete Durchschnitt hilft wirklich, zu entscheiden, ob es sinnvoll ist, in einer bestimmten Situation einzugreifen. Er ist daher ein Analysewerkzeug, das keinesfalls vernachlässigt werden sollte.