In diesem Artikel stellen wir dir drei nichtparametrische statistische Tests vor und erläutern anhand von Beispielen, in welchen Situationen sie eingesetzt werden können.
Nichtparametrische Tests: Du kennst den Student-Test, den Chi-Quadrat-Test oder den Fisher-Test, die alle parametrische Tests sind. Aber um parametrische statistische Tests zu verwenden, müssen wir bestimmte Annahmen über die Stichproben der Daten überprüfen (gleiche Varianzen zwischen den beiden Gruppen der gegebenen Stichproben, dass die Stichprobe einer Normalverteilung folgt…).
Manchmal können wir diese statistischen Annahmen nicht überprüfen oder sie sind nicht überprüfbar, dann verwenden wir nicht-parametrische statistische Tests!
Wilcoxon-Test für signierte Ränge
Dieser Test entspricht der nichtparametrischen Version des Student-Tests. Für den Student-Test benötigt man nämlich die Gaußsche Eigenschaft der Daten, die nicht unbedingt überprüft wird: Hier kommt dieser Test ins Spiel!
- Anwendungsfall:
Man hat eine Population, in der man ein Zufallsexperiment durchführt, und man möchte einen Vorher-Nachher-Vergleich durchführen, (Beurteilung der Herzfrequenz einer Population vor und nach der Injektion eines Medikaments),
Es liegen zwei gepaarte Stichproben vor. (Vergleich der Gehälter von Männern/Frauen gleichen Alters für die gleiche Stelle).
In Python verwenden wir die Funktion scipy.stats.wilcoxon aus der scipy-Bibliothek mit dem Modul stats.
- Beispiel:
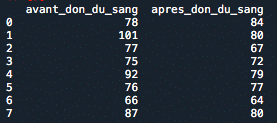
Wir haben einen Datensatz, der die Herzfrequenz vor und nach der Blutspende von 8 zufällig aus einer Population ausgewählten Personen misst. Wir listen in der folgenden Tabelle die Daten auf. Wir wollen herausfinden, ob die Herzfrequenz nach der Blutspende niedriger ist als vor der Blutspende, d. h. wir wollen den Test durchführen:
Nullhypothese H0: „Die Herzfrequenz ist vor und nach der Blutspende gleich“ und
Alternativhypothese H1: „Die Herzfrequenz ist nach der Blutspende niedriger als vor der Blutspende“.
Mann Whitney Test
Er entspricht der nicht-parametrischen Version des Student-Tests für zwei unabhängige Stichproben. Er wird auch Wilcoxon-Rangsummentest oder Wilcoxon-Mann Whitney-Test genannt.
- Anwendungsfälle:
Für voneinander unabhängige Stichproben. (Vergleich der Noten von zwei Klassen).
Auf Python benutzt man die Funktion scipy.stats.mannwhitneyu aus der scipy-Bibliothek mit dem Modul stats.
- Beispiel:
Eine Eisenbahngesellschaft möchte die Anzahl der Verspätungen für zwei Arten von Zügen vergleichen: A-Züge und B-Züge. In der folgenden Tabelle ist die Anzahl der Verspätungen für jeden Zug in Abhängigkeit von seinem Typ A oder B aufgelistet. Wir wollen herausfinden, ob einer der beiden Zugtypen dazu neigt, größere Werte anzunehmen als der andere.
Die Nullhypothese Ho: „Die Verspätungen für die beiden Zugtypen sind ähnlich“ und die Alternativhypothese H1: „Einer der beiden Zugtypen hat mehr Verspätungen als der andere“.
Kruskal Wallis Test
Dieser Test entspricht dem Mann-Whitney-Test für mehr als zwei Stichproben. Man kann ihn als nicht-parametrische Version der Anova betrachten (statistische Modelle, die zeigen, ob Gruppen zur selben Population gehören).
- Anwendungsfälle:
Vergleich der Weizenproduktion auf vier unabhängigen Feldern.
- Beispiel:
Die Eisenbahngesellschaft versucht, die Anzahl der Verspätungen jetzt für vier Zugtypen zu vergleichen: die Züge A, B, C und D. In der folgenden Tabelle ist die Anzahl der Verspätungen pro Zugtyp aufgelistet. Unser Ziel ist es, festzustellen, ob es signifikante Unterschiede bei den Verspätungen zwischen den verschiedenen Zugtypen gibt.
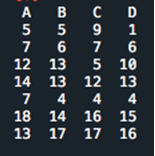
Die Nullhypothese Ho: „Alle Zugtypen haben ähnliche Verspätungen“ und die Alternativhypothese H1: „Einer der Zugtypen hat mehr/weniger Verspätungen als die anderen“.
In Python verwenden wir die Funktion scipy.stats.kruskal¶ aus der scipy-Bibliothek mit dem Modul stats.
Abschließend sei gesagt, dass man, wenn die statistischen Annahmen für die parametrischen Tests nicht überprüfbar oder nicht erfüllt sind, einen nichtparametrischen Test anwenden kann. Dies sind robustere Tests, die in vielen Situationen angewendet werden können, aber sie sind im Allgemeinen weniger aussagekräftig als parametrische Tests. Wenn du mehr über statistische Tests erfahren möchtest, gibt es in unserer Ausbildung zum Data Analyst oder Data Scientist ein Modul, das sich damit befasst.