Ein Modell erfüllt die Markov-Eigenschaft, wenn sein Zustand zu einem Zeitpunkt T ausschließlich vom Zustand zum Zeitpunkt T-1 abhängt. Kann man die Zustände des Modells zu jedem Zeitpunkt direkt beobachten, spricht man von einem beobachtbaren Markov-Modell. Sind die Zustände hingegen nicht direkt sichtbar, handelt es sich um ein verstecktes Markov-Modell (Hidden Markov Model). In diesem Artikel zeigen wir anhand von Beispielen, wie solche Modelle funktionieren und wofür Markov-Ketten eingesetzt werden.
Strenge mathematische Definition von Markov-Ketten
Mathematisch betrachtet ist eine Folge von Zufallsvariablen XnX_nXn, die Werte in einem Zustandsraum EEE annehmen, eine Markov-Kette, wenn sie die schwache Markov-Eigenschaft erfüllt. Diese wird durch folgende Gleichung beschrieben:
P(X_{n+1} = i_{n+1} | X_1 = i_1, ..., X_n = i_n) = P(X_{n+1} = i_{n+1} | X_n = i_n) Diese Formel besagt, dass die Übergangswahrscheinlichkeit in den zukünftigen Zustand in+1i_{n+1}in+1 nur vom aktuellen Zustand ini_nin abhängt – und nicht von der gesamten Abfolge vorheriger Zustände.
Die Schlüsselelemente einer Markov-Kette
Zustandsraum EEE: Die Menge aller möglichen Zustände, in denen sich das System befinden kann. Im meteorologischen Beispiel wäre das etwa E={Sonne,Wolken,Regen}E = \{\text{Sonne}, \text{Wolken}, \text{Regen}\}E={Sonne,Wolken,Regen}.
Übergangswahrscheinlichkeiten: P(Xn+1=j∣Xn=i)P(X_{n+1} = j \mid X_n = i)P(Xn+1=j∣Xn=i) gibt an, wie wahrscheinlich es ist, vom Zustand iii in den Zustand jjj zu wechseln.
Zeitliche Homogenität: Hängen diese Übergangswahrscheinlichkeiten nicht von der Zeit nnn ab, spricht man von einer homogenen Kette. Dieser Fall ist in der Praxis am weitesten verbreitet.
Diese formale Darstellung grenzt Markov-Ketten klar von anderen stochastischen Prozessen ab – und bildet das Fundament ihrer gesamten Theorie.
Geschichte und Grundlagen der Markov-Ketten

Markov-Ketten sind nach dem russischen Mathematiker Andreï Andreïevitch Markov (1856–1922) benannt. Er führte das Konzept 1902 ein, als er untersuchte, wie sich das Gesetz der großen Zahlen auf voneinander abhängige Größen erweitern lässt.
Ursprünglich wollte Markov herausfinden, wie Wahrscheinlichkeitsgrenzen auch dann bestimmt werden können, wenn die einzelnen Ereignisse nicht unabhängig sind – sondern nur vom jeweils vorhergehenden Ereignis abhängen, nicht jedoch von der gesamten Vergangenheit.
Die konzeptionelle Innovation
Seine zentrale Idee: Prozesse zu modellieren, bei denen die Zukunft nur durch die Gegenwart vom Vergangenen beeinflusst wird. Diese heute als Markov-Eigenschaft bekannte Annahme lässt sich knapp so ausdrücken: „Die Vergangenheit zählt nur, soweit sie den aktuellen Zustand geprägt hat.“
Markov selbst demonstrierte die Anwendbarkeit, indem er die Abfolge von Buchstaben in der russischen Literatur analysierte – insbesondere im Werk Eugen Onegin von Puschkin. Damit zeigte er, dass sich mathematische Konzepte auch auf sprachliche und andere nicht-mathematische Bereiche übertragen lassen.
Moderne Entwicklungen
Seitdem haben sich Markov-Ketten zu einem unverzichtbaren Werkzeug in zahlreichen Disziplinen entwickelt – von der statistischen Physik über die Ökonomie bis hin zur modernen künstlichen Intelligenz.
Beobachtbares Markov-Modell

Stell Dir vor, Du bist an einem verregneten Tag zu Hause eingesperrt und möchtest wissen, wie sich das Wetter in den nächsten fünf Tagen entwickeln wird.
Da Du kein Meteorologe bist, vereinfachst Du die Aufgabe und gehst davon aus, dass das Wetter einem Markov-Modell folgt: Der Wetterzustand an Tag J hängt nur vom Wetter am Vortag (J-1) ab.
Zur weiteren Vereinfachung nimmst Du an, dass es nur drei mögliche Wetterlagen gibt: Sonne, Wolken oder Regen. Basierend auf den Beobachtungen der letzten Monate erstellst Du ein Übergangsdiagramm mit den entsprechenden Wahrscheinlichkeiten:
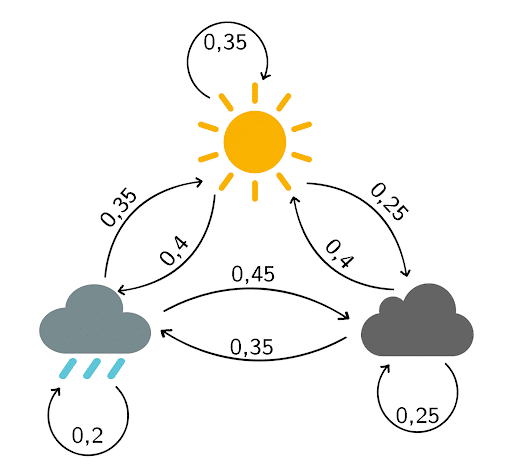
Die zugehörige Übergangsmatrix liest sich so:
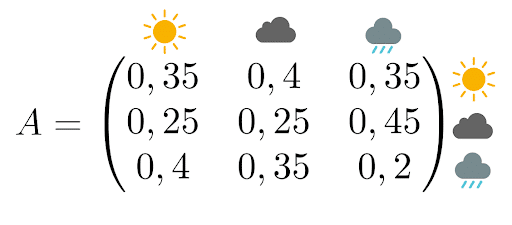
Wenn es heute regnet, liegt die Wahrscheinlichkeit für Sonne morgen bei 35 %.
Wenn es heute bewölkt ist, liegt die Wahrscheinlichkeit, dass es auch morgen bewölkt bleibt, bei 25 %.
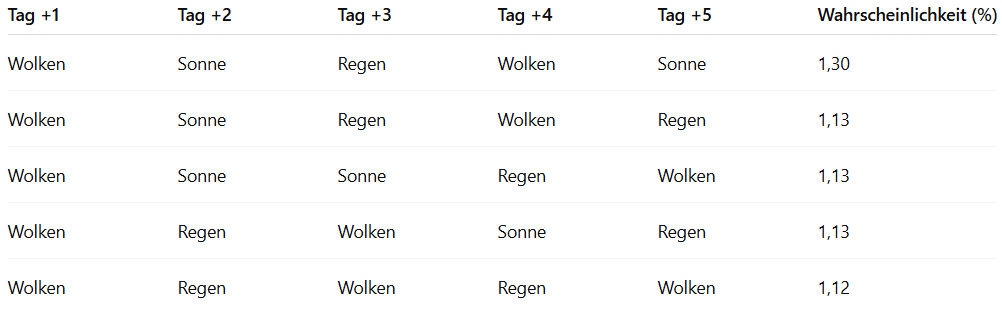
Nun möchtest Du berechnen, wie wahrscheinlich die konkrete Abfolge Sonne → Sonne → Regen → Wolken → Sonne ist.
Da im Modell nur der jeweilige Vortag zählt, genügt es, die entsprechenden Übergangswahrscheinlichkeiten miteinander zu multiplizieren (unter der Annahme, dass es heute regnet).
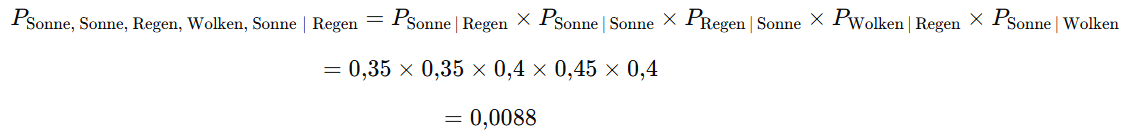
Dieses Verfahren lässt sich auf alle möglichen Wetterabfolgen anwenden. Die Kombination mit der höchsten Wahrscheinlichkeit ist dann die Vorhersage für die nächsten Tage.
In unserem Beispiel lassen sich so die fünf wahrscheinlichsten Wetterfolgen bestimmen.
Grundlegende Eigenschaften der Übergangsmatrix

Die im vorherigen Beispiel verwendete Übergangsmatrix besitzt einige zentrale mathematische Eigenschaften, die für das Verständnis von Markov-Ketten entscheidend sind.
Struktur der Matrix
Eine Übergangsmatrix P=(pij)P = (p_{ij})P=(pij) muss zwei Bedingungen erfüllen:
Nicht-Negativität: pij≥0p_{ij} \geq 0pij≥0 für alle i,ji, ji,j
Zeilensumme = 1: ∑jpij=1\sum_j p_{ij} = 1∑jpij=1 für alle iii
Die zweite Bedingung spiegelt wider, dass das System von jedem Zustand aus in einen der möglichen Zustände übergehen muss (einschließlich des Verbleibs im aktuellen Zustand).
Potenzen der Matrix – Mehrschritt-Prognosen
Ein zentrales Merkmal ist, dass PnP^nPn (die n-te Potenz von PPP) direkt die Übergangswahrscheinlichkeiten in n Schritten liefert.
Das Element (Pn)ij(P^n)_{ij}(Pn)ij gibt an, wie groß die Wahrscheinlichkeit ist, in genau nnn Schritten von Zustand iii in Zustand jjj zu gelangen.
Beispiel:
Mit P10P^{10}P10 erhält man die Wahrscheinlichkeiten für alle möglichen Zustandswechsel über einen Zeitraum von 10 Tagen.
Konvergenz zur stationären Verteilung
Unter bestimmten Bedingungen konvergieren die Potenzen der Matrix PPP gegen eine Grenzmatrix, deren Zeilen alle identisch sind.
Diese identische Zeile beschreibt die stationäre Verteilung – die langfristige Wahrscheinlichkeit für jeden Zustand, unabhängig vom Startpunkt.
In unserem Wetterbeispiel:
Nach vielen Tagen wird es einen konstanten Prozentsatz geben, wie oft Sonne, Wolken oder Regen auftreten, der sich nicht mehr verändert.
Klassifikation der Zustände in einer Markov-Kette

Sobald die Übergangsmatrix erstellt ist, lohnt es sich, das Langzeitverhalten der einzelnen Zustände zu untersuchen.
Daraus ergibt sich eine Klassifikation, die bei der Analyse der Kette entscheidend ist.
Transiente und rekurrente Zustände
Transient: Ein Zustand, den man möglicherweise nie wieder erreicht.
Rekurrent: Ein Zustand, der mit Sicherheit irgendwann erneut auftritt, unabhängig vom Startpunkt.
Beispiel:
Fügen wir im Wettermodell den Zustand „Sturm“ hinzu, aus dem man nur in „Regen“ gelangt und nie zurückkehrt, wäre „Sturm“ transient.
Absorbierende Zustände
Ein Zustand ist absorbierend, wenn pii=1p_{ii} = 1pii=1 gilt – man kann ihn nicht mehr verlassen.
Beispiel:
In einem Lebensdauermodell („juvenil“ → „erwachsen“ → „seneszent“ → „verstorben“) ist „verstorben“ absorbierend.
Irreduzible Markov-Ketten
Eine Markov-Kette ist irreduzibel, wenn jeder Zustand von jedem anderen aus erreichbar ist.
Das gewährleistet die Existenz einer eindeutigen stationären Verteilung.
Beispiel:
Im meteorologischen Modell kann man von „Sonne“ zu „Regen“ (über „Wolken“) und umgekehrt – daher irreduzibel.
Periodizität
Ein Zustand hat die Periode ddd, wenn er nur zu Zeitpunkten erreicht werden kann, die ein Vielfaches von ddd sind.
Bei d=1d = 1d=1 ist er aperiodisch.
Eine irreduzible und aperiodische Kette konvergiert immer zur stationären Verteilung.
Stationäre Verteilung und Konvergenz zum Gleichgewicht

Was ist eine stationäre Verteilung?
Eine stationäre Verteilung π\piπ ist ein Wahrscheinlichkeitsvektor, der sich durch die Anwendung der Übergangsmatrix PPP nicht verändert:
π=πP\pi = \pi Pπ=πP
Beispiel (Meteorologie):
Ist π=(0,4,0,3,0,3)\pi = (0{,}4, 0{,}3, 0{,}3)π=(0,4,0,3,0,3) für (Sonne, Wolken, Regen), bedeutet das:
langfristig 40 % Sonne
30 % Wolken
30 % Regen
unabhängig vom aktuellen Wetter.
Existenz und Einzigkeit
Für irreduzible Markov-Ketten mit endlichem Zustandsraum:
Existiert immer eine eindeutige stationäre Verteilung.
Das System zeigt langfristig ein stabiles, vorhersehbares Verhalten.
Der ergodische Satz
Für eine irreduzible und aperiodische Kette gilt:
Konvergenz:
Die Wahrscheinlichkeiten nähern sich unabhängig vom Startzustand der stationären Verteilung.Starkes Gesetz der großen Zahlen:
Der Anteil der Zeit, den das System in einem Zustand verbringt, entspricht langfristig der stationären Wahrscheinlichkeit.
Beispiel:
Hat eine Maschine eine stationäre Wahrscheinlichkeit von 0,950{,}950,95 für „funktionsfähig“, wird sie auf lange Sicht 95 % der Zeit einsatzbereit sein.
Praktische Anwendungen der Ergodizität
Industrielle Planung:
Verfügbarkeit, Auslastung und Wartungsintervalle lassen sich präzise abschätzen.Monte-Carlo-Simulationen:
Lange laufende Ketten liefern Stichproben, die der Zielverteilung folgen – Grundlage für viele moderne Sampling-Algorithmen.
Praktische Übungen zur Beherrschung von Markov-Ketten

Um das Verständnis zu festigen, folgen vier klassische Übungsaufgaben, jeweils mit Lösung.
Übung 1: Ehrenfestsches Urnenmodell
Eine Urne enthält 4 nummerierte Kugeln.
In jedem Schritt wird eine Kugel zufällig ausgewählt und in die andere Urne gelegt.
Der Zustand ist die Anzahl der Kugeln in der ersten Urne.
Frage:
Bestimme die Übergangsmatrix und die stationäre Verteilung.
Lösung:
Zustände: {0,1,2,3,4}\{0, 1, 2, 3, 4\}{0,1,2,3,4}
Wechselwahrscheinlichkeiten:
Von Zustand iii zu i−1i-1i−1: i/4i/4i/4
Von Zustand iii zu i+1i+1i+1: (4−i)/4(4-i)/4(4−i)/4
Stationäre Verteilung folgt einer Binomialverteilung: π(i) = C(4,i)/16, also π = (1/16, 4/16, 6/16, 4/16, 1/16).
Übung 2: Zufälliger Gang auf einem Graphen
Ein Spielstein bewegt sich auf einem Quadrat mit den Ecken A,B,C,DA, B, C, DA,B,C,D.
In jedem Schritt geht er gleich wahrscheinlich zu einer benachbarten Ecke.
Frage:
Ist die Kette irreduzibel?
Periodisch?
Mittlere Rückkehrzeit?
Lösung:
Irreduzibel: Ja – jede Ecke ist von jeder anderen erreichbar.
Periodizität: Ja, Periode d=2d=2d=2 (Rückkehr nur in gerader Schrittzahl).
Mittlere Rückkehrzeit: 444 Schritte.
Übung 3: Lebensdauer-Modell
Zustände: juvenil (J), reif (M), seneszent (S), verstorben (D).
J M S D
J [0.6 0.4 0 0 ]
M [0 0.7 0.3 0 ]
S [0 0 0.8 0.2]
D [0 0 0 1 ]
Frage:
Wahrscheinlichkeit, dass ein juveniler Organismus den Zustand „seneszent“ erreicht?
Lösung:
Jeder reife Organismus erreicht „S“ mit Sicherheit.
Wahrscheinlichkeit: 0.4×1=0.40.4 \times 1 = 0.40.4×1=0.4.
Übung 4: Absorptionszeit
Frage:
Erwartete Lebensdauer eines juvenilen Organismus?
Lösung:
Über das Fundamental Matrix Verfahren der absorbierenden Markov-Ketten:
Erwartungswert ≈8,33\approx 8{,}33≈8,33 Zeiteinheiten.
Diese Beispiele zeigen, wie Markov-Ketten in realen Szenarien angewendet werden – von einfachen Zufallsexperimenten bis zu komplexen Lebensdauer- oder Netzwerkmodellen.
Erweiterung auf kontinuierliche Markov-Ketten

Bisher haben wir diskrete Markov-Ketten betrachtet, bei denen Zustandsänderungen zu festen Zeitpunkten erfolgen (z. B. Tag 1, Tag 2 …).
In vielen Anwendungen können Übergänge jedoch jederzeit stattfinden – dies ist der Bereich der kontinuierlichen Markov-Prozesse.
Fundamentale Unterschiede zum diskreten Modell
Übergangsmatrix → wird ersetzt durch die infinitesimale Generator-Matrix Q=(qij)Q = (q_{ij})Q=(qij), die Übergangsraten beschreibt.
Übergangswahrscheinlichkeit im Zeitintervall dtdtdt:
Pij(dt)≈qij⋅dtP_{ij}(dt) \approx q_{ij} \cdot dtPij(dt)≈qij⋅dt
Beispiel: Call-Center
Ankunftsrate: λ=5\lambda = 5λ=5 Anrufe pro Stunde (Poisson-Prozess)
Service-Rate: μ=6\mu = 6μ=6 Anrufe pro Stunde (mittlere Bearbeitungszeit 10 Minuten)
Zustände: Anzahl der aktuell in Bearbeitung befindlichen Anrufe
Übergänge:
n→n+1n \to n+1n→n+1 mit Rate λ\lambdaλ (neuer Anruf)
n→n−1n \to n-1n→n−1 mit Rate nμn\munμ (Bearbeitung abgeschlossen)
Kontinuierliche Chapman-Kolmogorov-Gleichungen
dP(t) = P(t) * Q
P(t)P(t)P(t) = Matrix der Übergangswahrscheinlichkeiten zum Zeitpunkt ttt
QQQ = Generator-Matrix
Stationäre Verteilung im kontinuierlichen Modell
Im Gleichgewicht gilt:
π⋅Q=0\pi \cdot Q = 0π⋅Q=0
π\piπ = stationäre Verteilung
Flussgleichgewicht: Eintrittsrate = Austrittsrate für jeden Zustand
Typische Anwendungen
Systemzuverlässigkeit: Modellierung von Ausfällen (Rate λ\lambdaλ) und Reparaturen (μ\muμ)
Epidemiologie: SIR-Modelle mit kontinuierlichen Infektions- und Genesungsraten
Finanzwirtschaft: Diffusionsmodelle für Preisbewegungen
Vorteile gegenüber dem diskreten Modell
- Realistischere Abbildung kontinuierlicher Phänomene
- Oft elegantere analytische Berechnungen
- Grundlage für komplexere Modelle wie Diffusionsprozesse und stochastische Differentialgleichungen
Monte-Carlo-Methoden mit Markov-Ketten (MCMC)
Markov-Ketten sind das Fundament moderner statistischer Simulationstechniken – besonders, wenn Zielverteilungen zu komplex sind, um direkt daraus zu sampeln.
Grundprinzip von MCMC
Die geniale Idee besteht darin, eine Markow-Kette zu konstruieren, deren stationäre Verteilung exakt der Zielverteilung entspricht, aus der wir sampeln möchten. Lässt man die Kette ausreichend lange laufen, folgen die gewonnenen Stichproben näherungsweise dieser Zielverteilung.
Der Metropolis-Hastings-Algorithmus
Ziel: Sampling aus beliebigen Verteilungen π(x)\pi(x)π(x), selbst wenn nur bis auf eine Normierungskonstante bekannt.
Ablauf:
Ausgangszustand xtx_txt
Vorschlag yyy aus Vorschlagsverteilung q(y∣xt)q(y \mid x_t)q(y∣xt)
Berechne Akzeptanzwahrscheinlichkeit: α = min(1, [π(y)q(xₜ|y)] / [π(xₜ)q(y|xₜ)])
Akzeptiere yyy mit Wahrscheinlichkeit α\alphaα, sonst bleibe bei xtx_txt.
Eigenschaft: Stationäre Verteilung der Kette ist exakt π(x)\pi(x)π(x).
Anwendungen in der Bayes'schen Statistik
In der Bayes’schen Inferenz wollen wir aus der a-posteriori-Verteilung:
π(θ∣D)∝π(D∣θ)⋅π(θ)\pi(\theta \mid D) \propto \pi(D \mid \theta) \cdot \pi(\theta)π(θ∣D)∝π(D∣θ)⋅π(θ)
sampeln.
MCMC macht dies möglich, selbst wenn keine analytische Form existiert – und hat damit die moderne Statistik revolutioniert.
Gibbs-Sampling
Spezialfall von Metropolis-Hastings für mehrdimensionale Verteilungen
Aktualisiert jeden Parameter einzeln, bedingt auf die anderen
Besonders effizient bei graphischen Modellen (z. B. Bayes’sche Netzwerke)
Konvergenzdiagnose
Entscheidend ist zu prüfen, wann die Kette den Startzustand „vergessen“ hat.
Typische Methoden:
Trace Plots (Zeitreihendarstellung)
Gelman–Rubin-Statistik (R^\hat{R}R^-Kriterium)
Autokorrelationsanalyse
Zeitgenössische Anwendungen
Künstliche Intelligenz: Bayes’sche neuronale Netze zur Unsicherheitsquantifizierung
Epidemiologie: Parameteranpassung von SIR-Modellen an reale Daten
Finanzwirtschaft: Schätzung stochastischer Volatilitätsmodelle, Optionsbewertung
Markow-Ketten im Ökosystem der modernen Data Science

Im Zeitalter von Big Data und künstlicher Intelligenz haben Markow-Ketten ihren ursprünglichen theoretischen Rahmen weit hinter sich gelassen und prägen heute zahlreiche praxisnahe Anwendungen.
Natural Language Processing (NLP)
Frühe Sprachmodelle basierten auf Markow-Ketten – und waren damit die Vorläufer moderner Modelle wie GPT.
Typische Einsatzgebiete:
-
Automatische Textgenerierung: Sätze entstehen durch Verkettung von Übergangswahrscheinlichkeiten.
-
Rechtschreibkorrektur: Erkennung und Korrektur unwahrscheinlicher Zeichenfolgen.
-
Textklassifikation: Eigenes Markow-Modell pro Kategorie, z. B. Spam vs. Nicht-Spam.
Empfehlungssysteme
Plattformen wie Netflix oder Spotify modellieren Nutzerverhalten mit Markow-Ketten.
Zustände: konsumierte Inhalte
Übergänge: Wahrscheinlichkeit, von einem Inhalt zum nächsten zu wechseln
Ziel: präzise Vorhersage relevanter Empfehlungen
Zeitreihenanalyse im IoT
Sensoren im Internet der Dinge liefern kontinuierliche Datenströme.
Anwendungen:
Anomalieerkennung: Erkennen ungewöhnlicher Messmuster.
Predictive Maintenance: Vorhersage möglicher Ausfälle in Industrieanlagen.
Energieoptimierung: Analyse und Modellierung von Verbrauchsprofilen.
Cybersicherheit und Betrugserkennung
Markow-Ketten helfen, abweichendes Verhalten zu identifizieren.
Intrusion Detection: Erkennung verdächtiger Netzwerkaktivitäten.
Malware-Analyse: Klassifizierung anhand typischer Systemaufruf-Sequenzen.
Verhaltensbasierte Authentifizierung: Nutzererkennung über Navigationsmuster.
Digitales Marketing und Web Analytics
Optimierung von Nutzererfahrungen im Web.
Customer Journey Analyse: Verstehen von Konversionspfaden.
Sequenzielles A/B-Testing: Messen, wie Änderungen das Nutzerverhalten beeinflussen.
Marketing-Attribution: Beitrag einzelner Akquisekanäle quantifizieren.
Bioinformatik und Genomforschung
Von DNA-Sequenzen bis Krankheitsverlauf.
Genexpressionsanalyse: Modellierung zeitlicher Genaktivität.
Genomische Epidemiologie: Nachverfolgung viraler Mutationswege.
Personalisierte Medizin: Prognose individueller Krankheitsverläufe.
Integration mit Machine Learning
Markow-Ketten und moderne KI-Modelle ergänzen sich.
Feature Engineering – Extraktion von Merkmalen aus Sequenzen.
Reinforcement Learning – Entscheidungsprozesse basieren auf markovschen Zustandsmodellen.
RNN, LSTM, GRU – Erweiterung klassischer Modelle um dynamisches Gedächtnis.
Diese Anwendungen zeigen: Markow-Ketten sind kein reines Lehrbuchkonzept , sondern sie bilden ein zentrales methodisches Fundament für den Umgang mit sequenziellen Daten in der heutigen digitalen Wirtschaft.
Verstecktes Markow-Modell (HMM)

Die Grundannahmen bleiben dieselben wie bei einem klassischen Markow-Modell, jedoch mit einem entscheidenden Twist:
Der eigentliche Zustand (z. B. das Wetter) ist nicht direkt beobachtbar, sondern muss aus indirekten Signalen (Emissionen) erschlossen werden.
Stell Dir vor:
Ein meteorologisch exzentrischer Entführer sperrt Dich in einen fensterlosen Raum. Keine Sicht nach draußen – nur ein Computer und eine Lampe.
Die Lampe leuchtet jeden Tag in einer bestimmten Farbe, abhängig vom Wetter draußen.
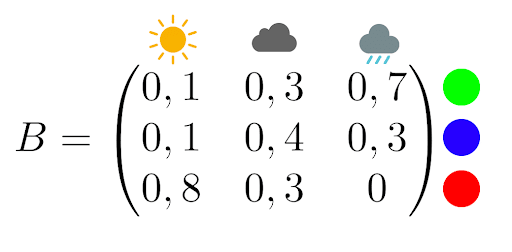
Er gibt Dir eine Beobachtungsmatrix, z. B.:
Wenn es regnet, leuchtet die Lampe zu 70 % grün und zu 30 % blau.
Für Sonne und Wolken gibt es ebenfalls festgelegte Wahrscheinlichkeiten.
Du darfst erst nach Hause, wenn Du das Wetter der nächsten fünf Tage korrekt vorhersagst – nur anhand der Lampenfarben.
Gegeben:
Am Tag vor Deiner Gefangenschaft hat es geregnet.
Beobachtete Lampenfarben in den fünf Tagen:
blau, blau, rot, grün, rot
Du baust ein verstecktes Markow-Modell mit:
Verdeckten Zuständen = Wetter: {Sonne, Wolken, Regen}
Emissionen = Lampenfarben: {Rot, Blau, Grün}
Übergangswahrscheinlichkeiten zwischen Wetterzuständen
Emissionswahrscheinlichkeiten für jede Farbe je Wetter

Mit einem Python-Programm oder per Hand mit dem Viterbi-Algorithmus berechnest Du die wahrscheinlichste Sequenz der Wetterzustände. Ergebnis:
[‚Bewölkt‘, ‚Bewölkt‘, ‚Sonnig‘, ‚Regen‘, ‚Sonnig‘]
HMMs zeigen, wie man aus indirekten Messungen (z. B. Sensor-, Log- oder Verhaltensdaten) die zugrunde liegenden Prozesse rekonstruiert – ein Prinzip, das in Spracherkennung, Biometrie, Bioinformatik und Predictive Maintenance unverzichtbar ist.
Tipp: Wer über einfache HMMs hinausgehen will, lernt in modernen Data-Science-Trainings, wie man mit Machine Learning Prognosen auf einem ganz neuen Level erstellt.
Vertiefung der Hidden Markov Models (HMM)
Unser Beispiel mit dem „meteorologischen Psychopathen“ bot einen spielerischen Einstieg in HMMs – doch diese Modelle sind weit mehr als ein Gimmick. Sie zählen zu den leistungsfähigsten Werkzeugen im statistischen Lernen und finden in zahlreichen Fachgebieten Anwendung.
Mathematische Struktur eines HMM
Ein Hidden-Markov-Modell besteht aus drei zentralen Elementen:
Versteckte Zustände
Die nicht direkt beobachtbare Zustandsfolge, z. B. das tatsächliche Wetter.Beobachtungen
Messbare Größen, z. B. Lampenfarben oder Sensordaten.Wahrscheinlichkeitsmatrizen
A – Übergangsmatrix: beschreibt die Wahrscheinlichkeiten, zwischen den versteckten Zuständen zu wechseln.
B – Emissionsmatrix: gibt an, mit welcher Wahrscheinlichkeit ein Zustand eine bestimmte Beobachtung erzeugt.
Die drei Kernprobleme der HMM-Theorie
Evaluierung
Fragestellung: Wie wahrscheinlich ist eine gegebene Beobachtungssequenz?
Lösung: Der Forward-Algorithmus berechnet diese Wahrscheinlichkeit effizient, ohne dass die Berechnung in einer kombinatorischen Explosion endet.Dekodierung
Fragestellung: Welche Abfolge versteckter Zustände ist am wahrscheinlichsten?
Lösung: Der Viterbi-Algorithmus nutzt dynamische Programmierung, um die plausibelste Sequenz zu bestimmen – z. B. die wahrscheinlichste Wetterabfolge basierend auf Lampenfarben.Lernen
Fragestellung: Wie lassen sich die Modellparameter aus Beobachtungsdaten schätzen?
Lösung: Der Baum-Welch-Algorithmus (eine Variante des EM-Algorithmus) passt die Matrizen A und B iterativ an, um die Beobachtungsdaten bestmöglich zu erklären.
Fortgeschrittene Anwendungen von HMMs
Automatische Spracherkennung
Versteckte Zustände = Phoneme, Beobachtungen = akustische Merkmale im Spektrogramm.Analyse biologischer Sequenzen
Identifikation von Genen: codierende/nicht-codierende Regionen als versteckte Zustände, Nukleotide (A, T, G, C) als Beobachtungen.Quantitative Finanzanalyse
Marktregime (bullish/bearish) als versteckte Zustände, Asset-Renditen als Beobachtungen; Erkennung von Regimewechseln zur Optimierung von Handelsstrategien.
Grenzen und Erweiterungen
Klassische HMMs nehmen an, dass Beobachtungen bei bekanntem Zustand unabhängig sind. In der Praxis kann dies zu vereinfachend sein.
Erweiterungen wie hierarchische HMMs oder rekurrente neuronale Netze (z. B. LSTM) überwinden diese Einschränkungen und ermöglichen kontextabhängigere Modellierungen.
Konkrete Anwendungen von Markow-Ketten

Markow-Ketten kommen in einer Vielzahl praxisrelevanter Bereiche zum Einsatz – weit über die klassische Wettervorhersage hinaus:
PageRank und Suchmaschinen
Googles PageRank-Algorithmus basiert auf einer Markow-Kette, um die Wichtigkeit von Webseiten zu bewerten. Jede Seite wird dabei als ein Zustand betrachtet, während die Hyperlinks zwischen den Seiten die Übergangswahrscheinlichkeiten definieren. Die Relevanz einer Seite ergibt sich aus ihrer Wahrscheinlichkeit in der stationären Verteilung der Kette. So entsteht eine objektive Rangfolge, die das Fundament der Suchergebnisse bildet.
Finanz- und Versicherungswesen
Auch im Finanz- und Versicherungsbereich sind Markow-Ketten weit verbreitet. Autoversicherer setzen sie beispielsweise ein, um Bonus-Malus-Systeme zu modellieren. Der Zustand repräsentiert hier die Bonusklasse eines Fahrers, während die Übergänge davon abhängen, wie viele Unfälle innerhalb eines Jahres gemeldet werden. Diese Modellierung erlaubt eine aktuarisch fundierte und faire Berechnung der Versicherungsprämien, basierend auf dem individuellen Risikoprofil.
Bioinformatik und Genetik
In der Bioinformatik und Genetik dienen Markow-Ketten, insbesondere versteckte Markow-Modelle (HMMs), zur Modellierung der Abhängigkeiten zwischen aufeinanderfolgenden Nukleotiden in DNA-Sequenzen. Damit lassen sich Gene identifizieren, Proteinstrukturen vorhersagen oder codierende Regionen im Genom lokalisieren. Die Kombination dieser mathematischen Modelle mit biologischem Fachwissen ermöglicht eine besonders präzise Analyse großer genetischer Datenmengen.
Industrielle Zuverlässigkeit
In der Industrie werden technische Systeme oft mithilfe von Markow-Ketten beschrieben, wobei die Zustände „funktionsfähig“, „defekt“ und „in Wartung“ typischerweise vorkommen. Dieses Modell erlaubt es, die Verfügbarkeit einer Anlage zu berechnen, Wartungsintervalle zu optimieren und Reparaturkosten nachhaltig zu reduzieren. So können Unternehmen ihre Betriebsprozesse effizienter und kostengünstiger gestalten.
Moderne künstliche Intelligenz
Auch in der modernen KI spielen Markow-Ketten eine Rolle, beispielsweise bei der Vorhersage des nächsten Wortes in einem Satz. Chatbots, Textgeneratoren und sogar Smartphone-Tastaturen nutzen dieses Prinzip, um kontextabhängige Vorschläge zu machen. Die Wahrscheinlichkeit für das nächste Zeichen oder Wort wird dabei direkt aus der aktuellen Sequenz abgeleitet, was die Interaktion natürlicher und flüssiger wirken lässt.
Warteschlangentheorie
In der Warteschlangentheorie, die etwa in Callcentern, Bankschaltern oder Serversystemen Anwendung findet, werden die Zustände durch die Anzahl wartender Kunden beschrieben. Die Modellierung mit Markow-Ketten ermöglicht es, Ressourcen präzise zu planen, Wartezeiten zu verkürzen und die Servicequalität zu verbessern – ein entscheidender Vorteil in stark frequentierten Serviceumgebungen.
Für alle, die tiefer einsteigen wollen: Unverzichtbare Referenzen zu Markow-Ketten

Die Theorie der Markow-Ketten ist ein reiches mathematisches Feld mit einer umfassenden akademischen Literatur. Je nach Ziel – ob theoretische Vertiefung oder praxisorientierte Anwendung – lohnt sich der Blick in ausgewählte Standardwerke und moderne Ressourcen.
Grundlegende Standardwerke
- Norris, J.R. – Markov Chains (Cambridge University Press, 1997)
Gilt als die moderne Referenz zum Thema. Streng, aber zugänglich. Ideal für ein solides mathematisches Fundament. - Sericola, Bruno – Chaînes de Markov – Théorie, algorithmes et applications (Hermes/Lavoisier, 2013)
Französisches Standardwerk mit starkem Fokus auf Algorithmen und praktische Anwendungen. - Baldi, Paolo et al. – Martingales et chaînes de Markov (Hermann, 2001)
Hervorragend zum Lernen mit vielen progressiv aufgebauten, vollständig gelösten Übungsaufgaben.
Fachspezifische Vertiefung
- Méléard, Sylvie – Modèles aléatoires en écologie et évolution (Springer, 2016)
Für Anwendungen in Biologie und Ökologie. Enthält stochastische Modelle von Populationen mit Markow-Ketten. - Brémaud, Pierre – Markov Chains, Gibbs Fields, Monte Carlo Simulation, and Queues (Springer, 1998)
Technisch anspruchsvolle Referenz zu Monte-Carlo-Methoden und Warteschlangentheorie.
Historische Schlüsseltexte
- Markov, A.A. – Extension of the law of large numbers to dependent quantities (1906)
Der Ursprungsartikel zum Konzept der Markow-Ketten. In englischer Übersetzung im Electronic Journal for History of Probability and Statistics verfügbar.
Didaktisch besonders empfehlenswert
- Grinstead, C.M. & Snell, J.L. – Introduction to Probability (AMS)
Sehr zugänglicher Einstieg, besonders das Kapitel zu Markow-Ketten. Mit interaktiven Online-Übungen. - Interaktive Übungsplattform WIMS (Université de Nice Sophia Antipolis)
Online-Aufgaben mit direktem Feedback – ideal zum Üben.
Moderne digitale Ressourcen
- Philippe Gay – Markow und Dornröschen (Images des Mathématiques, 2014)
Exzellenter populärwissenschaftlicher Artikel, der die Relevanz moderner Markow-Modelle auf unterhaltsame Weise vermittelt.
Diese Sammlung begleitet Lernende und Forschende vom ersten Einstieg bis hin zur forschungsnahen Spezialisierung – ganz gleich, ob der Fokus auf theoretischen Grundlagen, datengetriebenen Anwendungen oder algorithmischen Umsetzungen liegt.









