Viele Machine Learning Algorithmen erzielen gute Leistungen durch ihr Workout. Die große Mehrheit der Workouts basiert jedoch auf der Optimierung einer Verlustfunktion. Je kleiner der Wert dieser Funktion ist, desto besser sind die Ergebnisse des Algorithmus. Der Gradientenabstiegsalgorithmus ist eine von vielen Möglichkeiten, um das Minimum (oder Maximum) einer Funktion zu finden.
Eine erste intuitive Annäherung an diesen Algorithmus wurde in diesem Artikel gegeben.
Hier werden wir auf die mathematischen Grundlagen dieses Algorithmus eingehen und die Bedeutung der Lernrate erläutern.
Gradient Down: Mathematische Formalisierung
Der Gradientenabstieg ist einer der vielen sogenannten Abstiegsalgorithmen. Die allgemeine Formel lautet wie folgt:
xt+1 = xt – η∆xt
wobei η die Lernrate und ∆xt die Abstiegsrichtung ist. Diese Klasse von Algorithmen hat das Ziel, bei jeder Iteration ƒ(xt+1 ) ≤ ƒ (xt ) zu haben, wobei ƒ eine konvexe Funktion ist, die wir minimieren möchten.
Der Gradientenabstiegsalgorithmus beschließt, als Abstiegsrichtung dem Gegenteil des Gradienten einer konvexen Funktion f zu folgen, d.h. – Δƒ .
Warum ist das so? Der Gradient einer Funktion zeigt ihr maximales Wachstum von einem Punkt aus an. Die Wahl des Gegengradienten bedeutet, dass Sie den steilsten Anstieg wählen, um den Wert der Funktion zu minimieren. So funktioniert es :
- Es sei ein Initialisierungspunkt x0 , der zum Bereich von f gehört.
- Berechnen Sie f(xt ).
- Aktualisieren Sie die Koordinaten: xt+1 = xt – η Δ ƒ (xt ) (*)
- Wiederholen Sie 2 und 3 bis zum Abbruchkriterium.
Das Abbruchkriterium ist in der Regel ein Kriterium der Form |ƒxt+1 – ƒxt | ≤ ε , wobei der Wert sehr klein ist. Dieses Kriterium erscheint logisch, da man sich für einen Abbruch entscheidet, wenn der Unterschied zwischen den Werten der Funktion, die an zwei verschiedenen Punkten genommen werden, sehr wenig signifikant ist, was ein Zeichen dafür ist, dass man konvergiert hat. Ein anerkanntes Abbruchkriterium im Machine Learning ist die Anzahl der Iterationen; es wird eine endliche Anzahl von Optimierungen durchgeführt (Schritt 2 und 3).
Zwei Elemente, die auf den ersten Blick vernachlässigbar erscheinen, wenn man den Algorithmus betrachtet, sind in Wirklichkeit entscheidend für die gute Funktionsweise des Algorithmus; der Initialisierungspunkt x0 und der Wert der Lernrate η. Ein schlechter Initialisierungspunkt oder eine schlecht angepasste Lernrate kann den Algorithmus daran hindern, zum Minimum zu konvergieren. Je höher die Lernrate, desto weiter entfernt wird die Richtung verfolgt, die durch den Gradienten angezeigt wird. Dies kann dazu führen, dass wir in einem lokalen Minimum oder einem Sattelpunkt stecken bleiben oder das globale Minimum verfehlen. Wir werden anhand eines einfachen Beispiels den Einfluss der Lernrate auf die Leistung des Gradientenabstiegs untersuchen.
Bedeutung der Lernrate
Betrachten wir ein einfaches Beispiel einer linearen Regression. Es gibt eine Linie y=w0 *x+w1 . Wir haben n Beobachtungen, die einer linearen Beziehung folgen, und mit Hilfe dieser Beobachtungen versuchen wir, die richtigen Parameter zu finden, w und w0 1 , die diese Beziehung definieren. Wie bereits erwähnt, ist die Optimierung eines Modells, d.h. die Suche nach den besten Parametern, die zu einer guten Leistung führen, gleichbedeutend mit der Optimierung einer Verlustfunktion. Die Verlustfunktion, die in dieser Art von Situation am besten geeignet ist, ist die MSE,
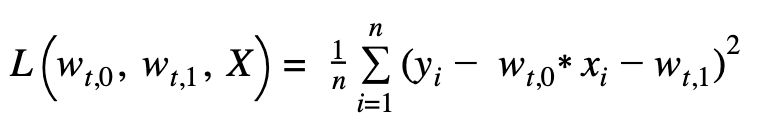
wobei t für die tième Iteration steht. Wenn Sie den Gradienten dieser Funktion berechnen und die Formel (*) anwenden, erhalten Sie die Formel für die Aktualisierung der Parameter :
Auf Code-Ebene ergibt sich daraus folgendes Ergebnis:
Wir variieren die Lernrate, um zu sehen, wie sie sich auf die Leistung des Modells auswirkt, und das über mehr als 100 Iterationen.
Eine geringe Lernrate?
Nehmen wir zunächst einen absichtlich kleinen Schritt von 0,01 an. Wir stellen fest, dass das Modell sehr lange braucht, um zu konvergieren. Nach 100 Iterationen sehen wir kaum noch, dass sich das Modell den Beobachtungen annähert.
In der dritten Grafik ist zu sehen, dass der Parameter w1 während der Optimierung stark variiert. Die letzte Grafik zeigt die langsame Veränderung der Verlustfunktion in Richtung ihres globalen Minimums. Dies ist ein Zeichen dafür, dass die Lernrate zu klein ist. Verändern wir sie in Richtung 0,99.
Eine hohe Lernrate?
Lassen Sie uns Grafik für Grafik analysieren. Die erste Grafik zeigt eine große Instabilität der linearen Approximation. Es ist zu erkennen, dass sie darüber und darunter liegt. Dies ist auf die instabile und plötzliche Änderung von w1 in der dritten Grafik zurückzuführen, die für die „Höhe“ der Linie in der Ebene verantwortlich ist. Woher kommt diese Instabilität? Die Antwort finden Sie in der 4.
Die hohe Rate bewirkt, dass der Verlust eine Art Ping-Pong-Effekt zwischen den beiden Seiten auf der Achse von w1 ausübt. Dieser Ping-Pong-Effekt verlangsamt den Rückgang des Wertes unserer Verlustfunktion. In der zweiten Grafik sehen wir, dass der Wert unseres Verlustes während der Iterationen lange Zeit hoch bleibt, da er in der Hälfte der Zeit nicht einmal auf der Grafik erscheint. Die Intuition sagt uns, dass wir den Wert senken sollten. Wir senken also die Rate auf 0,7 und beobachten das Ergebnis.
Ein besser angepasster Zinssatz
Diese Lernrate scheint optimal zu sein. In der letzten Grafik ist zu erkennen, dass der Wert der Verlustfunktion ab der ersten Iteration drastisch abnimmt, wie in der zweiten Grafik gezeigt wird. Das Modell nähert sich den Daten perfekt an, die Verlustfunktion stabilisiert sich bei 0, ihrem globalen Minimum, und die Parameter in Grafik 3 stagnieren, da sie optimal sind!
Die Komplexität der Lernrate
Wir haben festgestellt, dass die Lernrate eine entscheidende Rolle spielt. Eine zu hohe Lernrate kann dazu führen, dass man sehr lange um das Minimum schwankt oder es sogar verfehlt, während es bei einer zu geringen Lernrate sehr lange dauern kann, bis man konvergiert. Selbst eine zu hohe Lernrate kann zu einer Divergenz führen und das Ziel, das Minimum zu erreichen, verfehlen. Dasselbe Problem gilt für den Initialisierungspunkt. Zwei Initialisierungspunkte können zu zwei verschiedenen Ergebnissen führen, je nach der Komplexität der Verlustfunktion.
Hier hatten wir ein einfaches Modell mit zwei Parametern, was es uns ermöglichte, die Entwicklung des Modells zu visualisieren. In Wirklichkeit hat unser Modell viel mehr Parameter, was die Visualisierung unmöglich macht. Die Anpassung der Lernrate und die Wahl des Initialisierungspunktes sind in der Realität viel komplizierter. In der Praxis ist es notwendig, verschiedene Lernraten auf unser Modell anzuwenden, um zu sehen, welche die beste Leistung erbringt, ebenso wie der Initialisierungspunkt.
Hat Ihnen dieser Artikel gefallen? Abonnieren Sie unseren Newsletter, um regelmäßig weitere Informationen zu erhalten!









