Constraint Satisfaction Problems (CSPs) sind mathematische Probleme, bei denen eine Menge von Objekten eine Reihe von Beschränkungen erfüllen muss.
Diese Probleme, die in der Operationsforschung und der künstlichen Intelligenz viel Beachtung finden, erfordern spezielle Lösungsmethoden wie Backtracking oder Algorithmen zur Ausbreitung von Beschränkungen. Beispiele für berühmte Probleme, die durch ein CSP modelliert werden können, sind das Rucksackproblem, das Acht-Damen-Problem oder Sudoku.
Was ist Backtracking?
Backtracking ist eine Forschungstechnik, die komplexe Probleme löst, indem sie rekursiv Kombinationen von möglichen Entscheidungen untersucht, um zu einer Lösung zu gelangen. Sie wird häufig bei der Lösung von Such-, Optimierungs-, Planungs- und Spielproblemen eingesetzt. Backtracking basiert auf einer Tiefensuche, bei der Optionen so lange erforscht werden, bis eine Lösung gefunden wurde oder alle Möglichkeiten ausgeschöpft wurden.
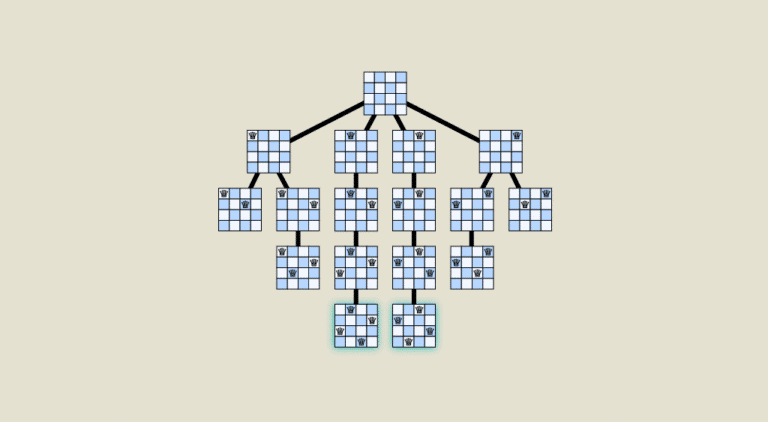
Baumförmige Datenstruktur
Backtracking basiert auf einer baumartigen Datenstruktur, bei der jeder Knoten einen Entscheidungsschritt bei der Lösung des Problems darstellt. Die Zweige des Baums stellen die verschiedenen Optionen oder Entscheidungen dar, die in jedem Schritt möglich sind. Während der Algorithmus fortschreitet, durchläuft er die verschiedenen Zweige des Baumes in der Tiefe, um zu bewerten, ob sie zu einer Lösung führen oder nicht.
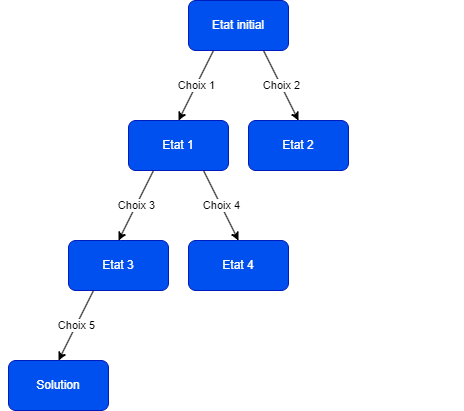
Ablauf des Algorithmus
Backtracking verfolgt einen rekursiven Ansatz zur Lösung eines Problems. Hier sind die verschiedenen Schritte zur Ausführung dieses Algorithmus:
- Schritt 1 – Auswahl: Der Algorithmus trifft zunächst eine Auswahl aus allen möglichen Optionen. Diese Wahl basiert auf dem aktuellen Zustand des Problems.
- Schritt 2 – Validierung: Nachdem der Algorithmus eine Auswahl getroffen hat, überprüft er, ob die Einschränkungen des Problems noch erfüllt sind. Wenn dies der Fall ist, kehrt er zu Schritt 1 zurück, um den Tiefgang fortzusetzen. Wenn dies nicht der Fall ist, geht er zurück (Backtrack), um eine andere Alternative auszuprobieren. Dies ist einer der Unterschiede zu grundlegenden Brute-Force-Lösungsalgorithmen: Backtracking kann Zweige eliminieren, ohne sie bis zum Ende durchsuchen zu müssen.
- Schritt 3 – Rückwärtsgehen (Backtracking): Wenn der Algorithmus zu irgendeinem Zeitpunkt feststellt, dass keine der Entscheidungen eines Zweiges zu einer Lösung führen wird oder dass er alle möglichen Optionen untersucht hat, ohne zu einem gültigen Endzustand zu gelangen, geht er zurück, um weitere Alternativen zu untersuchen. Dies bedeutet, dass du den Entscheidungsbaum zurückverfolgen musst, um andere, noch unerforschte Zweige zu durchlaufen.
- Schritt 4 – Lösung: Der Algorithmus durchläuft weiterhin den Zweig des Baumes und trifft Entscheidungen, indem er die Schritte 1 bis 3 wiederholt, bis er eine gültige Lösung erreicht. Eine Lösung wird im Allgemeinen als ein Endzustand des Problems definiert, der die gesetzten Beschränkungen oder Ziele erfüllt.
Anwendungsbeispiel für Backtracking
Um das Konzept des Backtracking zu veranschaulichen, nehmen wir ein konkretes Beispiel: das Lösen eines Sudoku-Rasters. In einem Sudoku-Spiel ist es das Ziel, ein 9×9-Gitter so auszufüllen, dass jede Zeile, jede Spalte und jedes 3×3-Untergitter alle Zahlen von 1 bis 9 ohne Wiederholungen enthält. Hier verwenden wir ein Raster der Größe 4×4, um die Illustration zu vereinfachen.
Backtracking kann zum Lösen eines Sudokus wie folgt verwendet werden:
Schritt 1 – Auswahl: Wähle zunächst ein leeres Feld im Gitter aus. Fülle dieses Feld mit einer möglichen Zahl (von 1 bis 4).
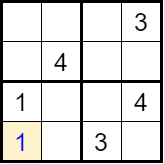
Schritt 2 – Validierung: Überprüfe, ob das Raster nach dieser Auswahl noch gültig ist. Wenn dies der Fall ist, gehe zu Schritt 1 zurück. Wenn nicht, gehe zurück, um eine andere Zahl in dem Feld auszuprobieren.
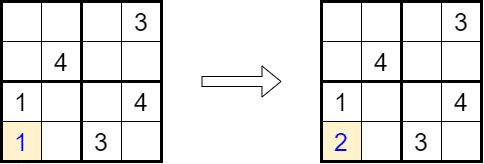
Hier entspricht die notierte 1 nicht den Regeln, also versuchen wir es stattdessen mit einer 2.
Schritt 3 – Backtracking: Wenn du zu irgendeinem Zeitpunkt keine gültige Zahl für ein Feld finden kannst, gehe zurück und versuche es mit einem anderen Wert im vorherigen Feld, usw.
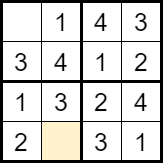
Hier kann man keine Zahl setzen und trotzdem die Regeln einhalten, also muss man die Zahl, die man direkt davor gesetzt hat, und die davor, wenn nötig, ändern.
Schritt 4 – Lösung: Wiederhole die Schritte 1 bis 3, bis alle Felder ausgefüllt sind und die Beschränkungen des Spiels überprüfen, was bedeutet, dass du eine gültige Lösung für das Sudoku gefunden hast.
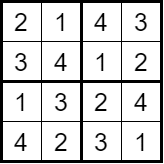
Vorteile des Backtracking
Backtracking hat als Problemlösungsansatz mehrere Vorteile:
- Vollständigkeit: Es stellt sicher, dass alle möglichen gültigen Lösungen untersucht werden, was es für die Suche nach optimalen Lösungen nützlich macht.
- Effizienz: Backtracking kann sich als sehr effizient erweisen, insbesondere bei Problemen mit starken Einschränkungen, wodurch einige Optionen schnell ausgeschlossen werden können.
- Anpassungsfähigkeit: Es kann auf eine Vielzahl von Problemen angewendet werden, da es auf einer allgemeinen Baumstruktur basiert.
Grenzen des Backtracking
Trotz seiner Vorteile hat das Backtracking einige Einschränkungen:
- Kombinatorische Explosion: Bei manchen Problemen kann die Anzahl der zu untersuchenden Kombinationen exponentiell ansteigen, wie z. B. beim Problem des Handlungsreisenden, bei dem die Berechnung eines Pfades zwar in 1 Mikrosekunde erfolgt, es aber fast zwei Jahrtausende dauert, um alle Pfade durch 20 Punkte zu berechnen.
- Komplexität: Die Implementierung von Backtracking kann komplex sein, insbesondere bei Problemen, bei denen die Definition von Entscheidungen, Einschränkungen und Abbruchkriterien kompliziert ist.
- Keine Konvergenzgarantie: Backtracking kann in bestimmten Fällen nicht zu einer Lösung konvergieren, z. B. wenn die Lösung nicht existiert, oder in Endlosschleifen stecken bleiben, wenn das Problem schlecht definiert ist.
Optimierung des Backtrackings
Es gibt verschiedene Techniken, um den Backtracking-Prozess zu optimieren, darunter :
- Heuristiken: Die Verwendung von intelligenten Regeln und Heuristiken, um die Suche zu den aussichtsreichsten Zweigen des Entscheidungsbaums zu leiten.
- Ausdünnen (pruning): Das frühzeitige Erkennen und Entfernen bestimmter Zweige des Baums, die nicht zu einer Lösung führen können, wodurch die kombinatorische Explosion reduziert wird.
- Memory: Das Speichern (Caching) der erforschten Zustände, um zu vermeiden, dass dieselben Konfigurationen mehrmals neu berechnet werden müssen, wenn sie auf mehrere verschiedene Arten gewonnen werden können.
Backtracking-Anwendungen in der KI
Backtracking wird in verschiedenen Bereichen der künstlichen Intelligenz und der Operationsforschung häufig eingesetzt. Hier sind einige Anwendungsbeispiele:
- Logikspiele: Das Lösen von Logikspielen, wie z. B. Sudoku, ist ein klassisches Beispiel für die Verwendung von Backtracking.
- Pfadsuche: Bei Pfadsuchproblemen, wie der Suche nach optimalen Pfaden in einem Graphen, kann Backtracking eingesetzt werden, um verschiedene Pfadoptionen zu erforschen.
- Schach und andere Brettspiele: In Brettspielen wie Schach kann Backtracking verwendet werden, um mögliche Handlungsfolgen zu bewerten und die beste Strategie zu wählen.

Fazit
Backtracking ist eine leistungsstarke Technik in der künstlichen Intelligenz, um komplexe Probleme zu lösen, indem systematisch die verschiedenen Kombinationen von möglichen Handlungen oder Entscheidungen erforscht werden. Es basiert auf einer Entscheidungsbaumstruktur und folgt einem iterativen Prozess der Auswahl, Bestätigung und Rückbesinnung.
Backtracking hat zwar Vorteile, kann aber auch mit dem Problem der kombinatorischen Explosion konfrontiert werden und erfordert oft Optimierungstechniken, um effektiv zu sein. Es wird häufig in Bereichen wie Spielen, Planung, Pfadsuche und Rätsellösungen eingesetzt und zeigt damit seine Vielseitigkeit bei der Lösung komplexer Probleme in der künstlichen Intelligenz.
Wenn du dich in Data Science und künstlicher Intelligenz weiterbilden möchtest, dann schau dir unsere Fortbildung zum Data Scientist an.