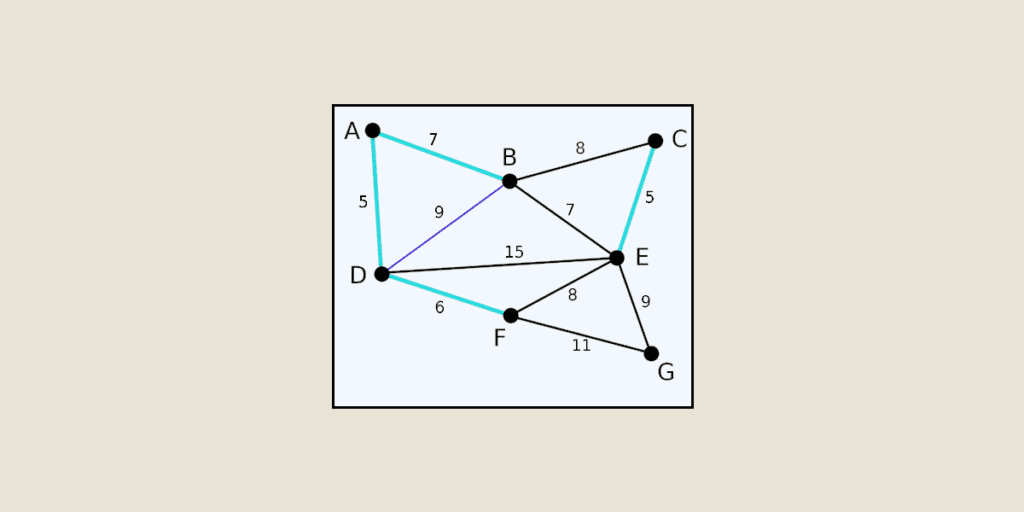
Der Kruskal-Algorithmus optimiert die Verbindungen innerhalb eines Netzwerks und ist eines der wichtigsten Konzepte im Bereich des maschinellen Lernens. Finde heraus, wie er funktioniert und wie nützlich er im Alltag ist.
Was ist der Kruskal-Algorithmus?
Der Kruskal-Algorithmus wurde 1956 von Joseph Kruskal entwickelt und dient dazu, in einem gewichteten, nicht-orientierten, zusammenhängenden Graphen einen minimal gewichteten Baum (ARPM) zu finden (auch Minimum Covering Tree (ACM) oder Minimum Subtendent Tree genannt).
Bevor wir ins Detail gehen, sollten wir die folgenden Begriffe definieren:
- Baum: Er steht für einen zusammenhängenden, zyklenfreien (oder azyklischen) Graphen.
Zusammenhängender Graph: Das bedeutet, dass es einen Pfad gibt, über den man von jedem anderen Scheitelpunkt des Graphen aus auf alle Scheitelpunkte zugreifen kann. - Azyklischer Graph: Das bedeutet, dass der Zyklus unterbrochen wird, um auf alle Scheitelpunkte zuzugreifen.
- Gewichteter Graph: Jede Kante hat ein Gewicht.
- Ungerichteter Graph: Jede Kante kann in beide Richtungen durchlaufen werden.
- Überlappender Baum: Er verweist auf eine Menge von Kanten eines gewichteten Graphen, der alle Eckpunkte (aber nicht unbedingt alle Kanten) enthält. Das Gewicht des überdeckenden Baums ist die Summe der Gewichte seiner Kanten.
- Minimal gewichteter überlappender Baum (ARPM): Dies ist ein überlappender Baum, dessen Gewicht so klein wie möglich ist. Das heißt, er ist eine Teilmenge von Kanten, die alle Knoten des Graphen verbindet, bei denen die Summe der Kantengewichte so gering wie möglich ist.
Das Ziel des Kruskal-Algorithmus ist es, einen solchen überlappenden Baum mit minimalem Gewicht zu finden.
💡Gut zu wissen: Neben dem Kruskal Algorithmus kann man auch den Prim-Algorithmus verwenden, um einen ARPM zu finden.
Wie funktioniert der Kruskal Algorithmus?
Die Schritte des Kruskal Algorithmus
Um den überlappenden Baum mit dem geringsten Gewicht zu finden, sieht der Kruskal-Algorithmus die folgenden Schritte vor:
- Sortiere die Kanten (a) des Graphen (G) nach steigendem Gewicht. Dabei werden die leichtesten Kanten zuerst untersucht.
- Von einem leeren Baum (T) ausgehen. Das heißt, ein Baum, der keine Kanten enthält; sein Gewicht ist gleich 0. Er wird schrittweise aufgebaut, indem man die folgenden Schritte befolgt.
- Wähle die Kanten nach steigendem Gewicht aus. Man sollte also mit den leichtesten Kanten beginnen. Wenn das Hinzufügen einer Kante nicht bedeutet, dass ein Zyklus im Graphen entsteht, sollte sie dem Baum hinzugefügt werden.
- Wiederhole den Vorgang, bis alle Eckpunkte (S) miteinander verbunden sind. Dies geschieht, ohne einen Zyklus in der ARPM zu erzeugen.

Mathematische Übersetzung
In der Mathematik wird der Kruskal-Algorithmus wie folgt übersetzt:
T = ø
Sortiere die a in G nach aufsteigenden Werten.
F = { ao }
Wiederhole F = { ao } solange, bis alle S in T aufgenommen wurden.
Wobei
ao: die kleinste nicht untersuchte Kante.
T: Überlappender Baum mit minimalem Gewicht
G: Graph
S: Scheitelpunkt
p: die Anzahl der Kanten, die bereits im G-Graphen platziert sind.
n: die Anzahl der Gipfel im Graphen G.
F = { ao } :Hinzufügen der kleinsten nicht untersuchten Kante
Gut zu wissen: Die Anzahl der Kanten eines ARPM kann um (n-1)n/2 variieren. Je weniger Kanten der überlappende Baum mit dem geringsten Gewicht enthält, desto schneller ist der Kruskal-Algorithmus.
Warum sollte man den Kruskal-Algorithmus verwenden?
In der Praxis wird dieser Algorithmus oft verwendet, um praktische Probleme zu lösen, wie z. B. die Gestaltung von Kommunikationsnetzen zu möglichst geringen Kosten, die Planung von Verkabelungen, die Beseitigung von weniger rentablen Seeverbindungen bei gleichzeitiger Wahrung der Erreichbarkeit der verschiedenen Häfen usw.
Unabhängig von der konkreten Anwendung ermöglicht der Kruskal-Algorithmus eine Optimierung der Verbindungen. Genau aus diesem Grund ist er im Machine Learning besonders nützlich.
Indem er die Gewichtung der Verbindungen optimiert, kann er die Effizienz von Modellen des maschinellen Lernens maximieren.
Gut zu wissen: Du kannst den Kruskal-Algorithmus in verschiedenen Programmiersprachen wie C++, Python, Java, C#, Javascript usw. verwenden.
Vertiefe dein Wissen über Machine Learning mit DataScientest
Über den Kruskal-Algorithmus hinaus erfordert Machine Learning das Beherrschen einer Vielzahl von mathematischen und statistischen Konzepten, Programmiersprachen, Big-Data-Tools, Datenvisualisierung etc. All diese technischen Fähigkeiten können nur durch eine umfassende Ausbildung erlernt werden. So wie die von DataScientest angebotene. Entdecke unser Programm.