Quicksort ist einer der besten Sortieralgorithmen, der bei großen Datenstrukturen wie Listen und Tabellen eingesetzt wird. Im Folgenden erfährst du, wie dieser Algorithmus funktioniert, welche verschiedenen Anwendungsfälle es gibt und wie leistungsfähig er ist.
Die Schnellsortierung oder Pivot-Sortierung ist ein Sortieralgorithmus, der 1961 von Tony Hoare erfunden wurde, als er als Gaststudent an der Moskauer Staatsuniversität studierte.
Zu den bekanntesten und am häufigsten verwendeten Sortieralgorithmen der Welt gehört auch die Quicksort. Quicksort ist eine Sortiertechnik, die verwendet wird, um die Elemente einer Datenstruktur in einer bestimmten Reihenfolge (aufsteigend oder absteigend) anzuordnen. Sie wird in der Regel bei Tabellen verwendet, kann aber auch bei Listen eingesetzt werden. Dieser Sortieralgorithmus basiert hauptsächlich auf dem DPR-Ansatz (Dividieren und Herrschen), bei dem zwei oder mehr Arrays mit einer Größe, die strikt kleiner als n ist, verwendet werden, um ein Sortierproblem für ein Array der Größe n zu lösen.
Bei der Schnellsortierung wird von Anfang an ein Element des zu sortierenden Arrays ausgewählt, das als Pivot bezeichnet wird, manchmal zufällig oder auf bestimmte Weise (normalerweise das erste Element oder das letzte Element des Eingabe-Arrays).
Anschließend muss die Eingabetabelle um den Pivot herum partitioniert werden, indem der Pivot an seiner entsprechenden Position in der sortierten Tabelle, d. h. seiner endgültigen Position, platziert wird: Dies wird durch eine Partitionierungsfunktion gewährleistet.
Der Partitionierungsalgorithmus ist ein iterativer Algorithmus, der die gesamte zu sortierende Tabelle durchläuft, um alle Elemente, die kleiner als der Pivot sind, links von diesem zu platzieren und alle Elemente, die größer als der Pivot sind, rechts von diesem zu platzieren.
Alles über den Quicksort-Algorithmus
Die Partitionierungsfunktion durchläuft iterativ die zu sortierende Tabelle, um die einzelnen Elemente mit dem Pivot zu vergleichen. Wenn ein Element gefunden wird, das kleiner als der Pivot ist, wird die Position dieses Elements mit dem Wert eines größeren Elements, das vor ihm in der Liste auftaucht, geändert. Wenn man auf ein Element stößt, das größer als die Pivotlinie ist, tut man nichts.
Als Ergebnis der Partition erhält man den Index des Pivots in der sortierten Tabelle, der somit sein endgültiger Index ist, und man tauscht somit die Anfangs- und Endposition des Pivots aus.
Die Wahl des Pivots ist entscheidend, da die Partitionierung der Datenstruktur um den Pivot herum durchgeführt wird. Wenn der Pivot die Tabelle nicht in zwei annähernd gleich große Untertabellen aufteilt, d.h. wenn der Pivot nicht mehr oder weniger dem Median entspricht, sondern einem Grenzwert der zu sortierenden Menge, wird die Partitionierung eine leere Menge der Größe und eine Menge der Größe n-1 ergeben, wenn die Anfangsgröße n war.
Im ersten Schritt erfordert diese Aufteilung n Operationen. Im nächsten Zug erfordert sie n-1, dann n-2, bis nichts mehr zum Sortieren übrig ist, was genau dem Prinzip der Auswahlsortierung entspricht, die eine quadratische Komplexität hat.
Eine allgemein akzeptierte Idee ist es, den Median von drei zufälligen Werten aus der Tabelle als Pivot zu nehmen, um die Situation der Wahl des falschen Pivots zu vermeiden.
Was ist zu tun, nachdem du die Endposition des Pivots nach der Partitionierungsfunktion erhalten hast?
Nachdem du die Endposition des Pivots erhalten und die Indizes ausgetauscht hast, musst du die Schnellsortierfunktion auf die beiden Untertabellen anwenden, die du auf beiden Seiten des Pivots erhalten hast.
Das heißt, die linke Untertabelle, die durch Array[Start,Pivot(Index)-1] markiert ist, und die rechte Untertabelle, die durch Array [Pivot(Index)+1,Ende] markiert ist, wobei Pivot(Index) dem Pivot-Index entspricht, den du nach der Partitionierungsfunktion für die Eingangstabelle erhalten hast.
Als Nächstes müssen wir zwei Pivots auswählen, die den Pivots der linken und rechten Untertabelle entsprechen, und dann einen rekursiven Aufruf der Funktion zum schnellen Sortieren auf diese beiden Untertabellen anwenden. Die rekursiven Aufrufe der Quicksort-Funktion werden entweder beendet, wenn der Start- und der Endindex eines Unterarrays gleich sind, was bedeutet, dass das Array nur ein Element enthält und somit bereits sortiert ist, oder wenn der Startindex eines Unterarrays größer ist als sein Endindex, was bedeutet, dass das Array kein Element enthält (leeres Array) und somit ebenfalls sortiert ist.
Illustration der Schnellsortierung / Quicksort
Betrachte zur Veranschaulichung das folgende Array, bei dem der Pivot als das am weitesten rechts stehende Element gewählt wurde, d. h. array[length(array)-1] = 4:
array = [9, 12, 1, 5, 6, 13, 8, 2, 4]
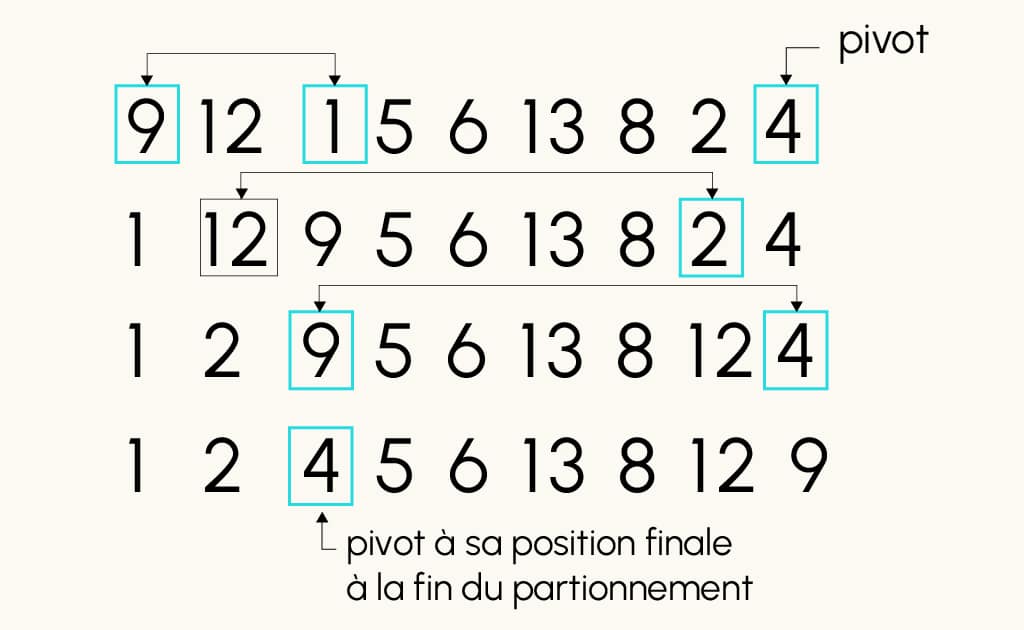
- Durch Anwendung der Funktion partition(array, 0, len(array)-1) erhält man:
Partitioniertes Array: 1 2 4 5 6 13 8 12 9 wobei der Pivot an seine Endposition in der sortierten Tabelle verschoben wurde.
- Anschließend wenden wir die Funktion quicksort auf die beiden Arrays an, die wir auf beiden Seiten des Pivots erhalten:
array1 = [1, 2]
array2 = [5, 6, 13, 8, 12, 9].
Außerdem musst du für jeden dieser Arrays einen Pivot auswählen und dann die Partitionen durchführen, bis sie sortiert sind.
Nach der Ausführung der Funktion quicksort erhält man die folgende Tabelle:
Sorted Array : 1 2 4 5 6 8 9 12 13 In Bezug auf die Komplexität ist im besten und im mittleren Fall eine fast lineare Komplexität in O(nlogn) zu beobachten. Im schlimmsten Fall hat die Schnellsortierung jedoch eine quadratische Komplexität, d. h. in O(n^2), was unbefriedigend ist. Eine quadratische Komplexität ist in diesem Algorithmus zu beobachten, wenn das Array bereits sortiert oder fast sortiert ist.
Demonstration der Komplexität des schnellen Sortierens / Quicksort im mittleren Fall
Ausgehend von der im mittleren Fall erfüllten Rekursionsgleichung kann man zeigen, dass die Komplexität nahezu linear ist, wie der folgende Beweis zeigt: Um ein Problem der Größe n zu lösen, löst man zwei Probleme der Größe n/2 mit einer linearen Rekonstruktion aufgrund der Partitionierungsfunktion, die linear zur Größe der Datenstruktur ist.
wobei O(n) die Komplexität der Partitionsfunktion darstellt
Wenn du n = 2 k setzt, erhältst du k = log 2 n
Nun stellt T(1) die Komplexität des schnellen Sortierens dar, wenn das Array nur ein einziges Element enthält und somit sortiert ist.
Warum ist das schnelle Sortieren / Quicksort so wichtig?
Die schnelle Sortierung / Quicksort ist aus Gründen der Datenlokalität im Durchschnitt effizienter als eine andere. Das liegt daran, dass jeder Aufruf mit Daten arbeitet, die im Speicher sehr nahe beieinander liegen. Aufgrund der Caches, die erhebliche Optimierungen ermöglichen, wenn die Daten eine hohe Lokalität haben, weist der Algorithmus eine bessere Leistung auf.
Was die räumliche Komplexität angeht, so hat die Schnellsortierung im schlimmsten Fall eine quadratische Komplexität und im mittleren Fall eine logarithmische Komplexität. Die Schnellsortierung ist effizient bei großen Datenstrukturen und hat eine geringe räumliche Komplexität. Dafür ist sie bei kleinen Strukturen weniger effizient als z. B. die Einfügesortierung.
Zusammenfassend lässt sich sagen, dass Quicksort ein häufig verwendeter Sortieralgorithmus ist, insbesondere bei großen Datenstrukturen, der im mittleren Fall eine gute zeitliche Komplexität aufweist. Die Wahl des Pivots bei der Verwendung dieses Algorithmus bleibt jedoch ein entscheidender Faktor, was folglich eine angemessene Wahl des Pivots erfordert.









