Möchtest du wissen, ob der Notendurchschnitt zwischen zwei Klassen sich voneinander unterscheidet? Oder wissen, ob die Umweltverschmutzung in einer Stadt über einem zulässigen Wert liegt? Wie können Sie die Wirksamkeit einer neuen Behandlung in einer Population testen? Hier setzen wir statistische Tests ein! Datascientest zeigt dir die Methode, um einen statistischen Test in 5 Schritten durchzuführen, mit einem Beispiel zur Unterstützung.
Was ist ein statistischer Test?
Ein statistischer Test dient dazu, eine Entscheidung zwischen zwei Hypothesen zu treffen. Ausgehend von der statistischen Hypothese und einer Datenprobe soll eine bestimmte Fragestellung beantwortet werden.
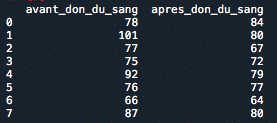
In diesem Artikel gehen wir von folgendem Experiment aus: Wir haben einen Datensatz, der die Herzfrequenz vor und nach einer Blutspende von 8 zufällig aus einer Population ausgewählten Personen misst. Wir listen in der folgenden Tabelle die Daten auf. Wir wollen herausfinden, ob die Herzfrequenz nach oder vor der Blutspende niedriger ist.
Schritt 1: Definiere die Nullhypothese und die Alternativhypothese
Die Nullhypothese Ho entspricht einem Nichteffekt des Experiments. Im Allgemeinen kann dies die Gleichheit von statistischen Parametern wie Mittelwert oder Varianz von zwei ausgewählten Stichproben aus einer Population sein. Dies wird verworfen oder akzeptiert.
Die Alternativhypothese H1 ist die Hypothese, die gezeigt werden soll. In der Regel ist sie eine „Gegen“- oder „Gegen“-Hypothese zur Nullhypothese. Sie besagt, dass der für die Nullhypothese verwendete Parameter entweder größer, kleiner oder anders ist.
In unserem Beispiel wollen wir herausfinden, ob die Herzfrequenz durch das Blutspenden sinkt. Daher definieren wir die Hypothesen Ho: „Die Herzfrequenz ist vor und nach dem Blutspenden gleich“ und H1: „Die Herzfrequenz ist nach dem Blutspenden niedriger als vor dem Blutspenden“.
Schritt 2: Der Fehler erster und zweiter Art und die Potenzfunktion
Bei einem statistischen Test muss man sich darüber im Klaren sein, dass man sich des Ergebnisses nie zu 100 % sicher sein kann. Es besteht immer die Gefahr, dass man sich irrt.
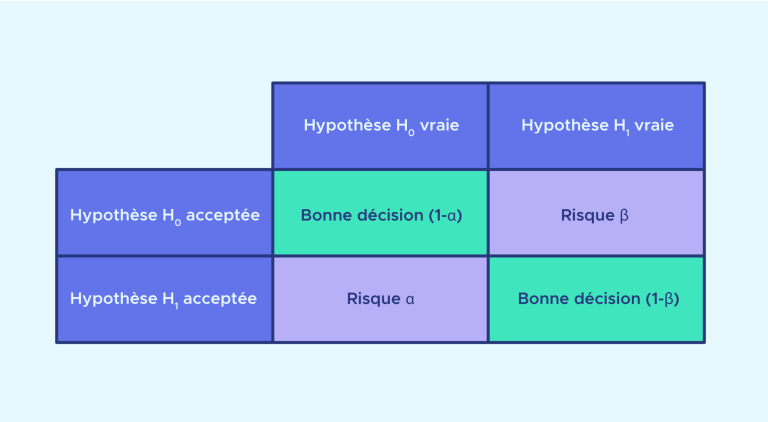
Der Fehler erster Art Alpha entspricht dem Risiko, die Nullhypothese Ho abzulehnen, obwohl sie wahr ist: Er ist ein „falsches Negativ“.
Der Beta-Fehler zweiter Art entspricht dem Risiko, die Nullhypothese anzunehmen, obwohl sie falsch ist: Er ist ein „falscher Positiver“ .
Die Potenzfunktion ist das Risiko, Ho abzulehnen, obwohl man Ho eigentlich ablehnen müsste.
Standardmäßig wird der Parameter Alpha auf 5% gesetzt: d. h. die maximale Wahrscheinlichkeit, HO abzulehnen, wenn sie wahr ist, beträgt 5%.
Bei der Konstruktion eines Tests wird vorgeschrieben, dass der Fehler erster Art der größte zu berücksichtigende Fehler ist. Daher wählt man aus allen Tests, deren Fehler erster Art eher gering ist, diejenigen aus, deren Fehler zweiter Art möglichst klein ist.Übersichtstabelle zu Fehlern erster und zweiter Art
Schritt 3: Wahl zwischen einseitigem und zweiseitigem Test
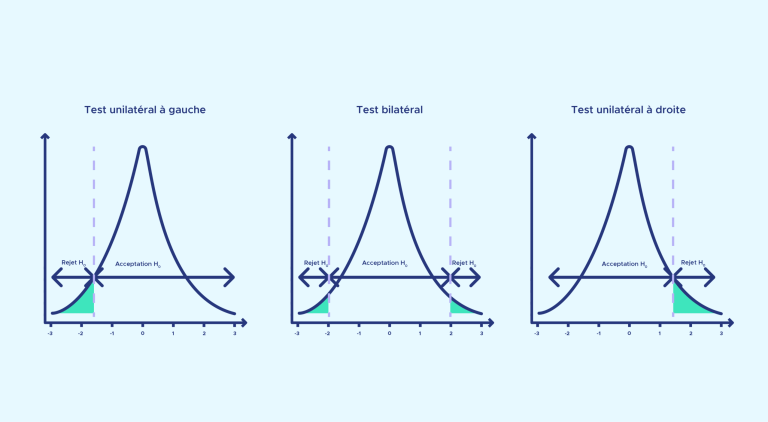
Es gibt zwei Haupttypen von Tests: einseitige oder zweiseitige Tests, die von der Definition der Hypothesen abhängen werden.
- Ein einseitiger Test ist ein statistischer Test, bei dem der Parameter der Alternativhypothese entweder kleiner oder größer als ein Referenzwert ist, z. B. wenn wir die Mittelwerte von zwei Stichproben A und B nehmen, ist dies mA > mB oder mA< mB.
- Ein zweiseitiger Test ist ein statistischer Test, bei dem der Parameter der Alternativhypothese unterschiedlich sein wird, ohne ein bekanntes Vorzeichen (mA = ! mB ).
In unserem Beispiel lautet unsere Alternativhypothese H1: „Die Herzfrequenz ist nach der Blutspende niedriger als vor der Blutspende“. Dies entspricht einem einseitigen Test. Wenn die Alternativhypothese H1 wäre: „Die Herzfrequenz ist vor und nach der Blutspende unterschiedlich“, dann wäre dies ein zweiseitiger Test.
Bei Python verwenden wir für alle statistischen Tests das Modul Stats der Bibliothek Scipy.
Alle statistischen Testfunktionen haben das alternative Argument, um den Typ anzugeben:
- Alternative = {“ greater“} / {„less“} für einen einseitigen Test,
- Alternative= {„two-sided“} für einen zweiseitigen Test (Standard, wenn nichts angegeben ist).
Schritt 4: Auswahl des geeigneten Tests
Dies ist ein sehr wichtiger Schritt, da eine falsche Wahl des Tests zu einer Fehlinterpretation der Ergebnisse führen kann.
Es gibt mehrere Kriterien, die hinsichtlich dieser Wahl zu berücksichtigen sind, insbesondere:
- die Größe der Stichprobe,
- die Unabhängigkeit zwischen den Gruppen,
- Arten von Variablen: quantitativ/qualitativ/kategorial.
Es gibt auch zwei Hauptarten von statistischen Tests: parametrische und nichtparametrische Tests.
Parametrische Tests sind Tests, bei denen die Stichprobe, die wir untersuchen, einer bestimmten Gesetzmäßigkeit (z. B. der Normalverteilung) folgt oder eine bestimmte Anzahl von Annahmen überprüft (gleiche Varianz zwischen den beiden gegebenen Stichproben). Sie sind leistungsstärker, erfordern aber eine bestimmte Anzahl von Annahmen, die überprüft werden müssen.
Wenn die Stichprobe, die uns zur Verfügung steht, die gegebenen Annahmen nicht bestätigt, dann wenden wir einen nichtparametrischen Test an. Dies sind robustere Tests, die in vielen Situationen gültig sind.
In unserem Beispiel wenden wir den Wilcoxon-Test für signierte Ränge an :
Schritt 5: Analyse der Ergebnisse
Nachdem wir den Test ausgewählt und ausgeführt haben, erhalten wir als Ausgabe mehrere Daten und insbesondere den p-Wert. Das ist der Wert, der uns erlaubt, den Test zu beantworten. Der p-Wert ist das Niveau, ab dem wir anfangen, Ho abzulehnen.
Wenn p-Wert < Alpha, dann lehnen wir Ho auf Alpha-Niveau ab,
Wenn p-Wert > Alpha, dann behalten wir Ho auf Alpha-Niveau bei.
Je kleiner der beobachtete p-Wert ist, desto eher möchte man Ho ablehnen, denn das bedeutet, dass der Wert der für den Test verwendeten Statistik für Ho untypisch ist.
Achtung! Der p-Wert ist nicht die Wahrscheinlichkeit, dass die Testhypothese wahr ist. Der p-Wert gibt an, inwieweit die Daten mit der Testhypothese und ihren Annahmen übereinstimmen. (Quelle wikipedia)
So können wir nun die Nullhypothese ablehnen oder beibehalten und somit unseren Test abschließen. In unserem Beispiel erhalten wir einen p-Wert von 0,039 < 0,05, also lehnen wir Ho auf dem Alpha-Niveau = 0,05 ab, also „Die Herzfrequenz ist nach der Blutspende niedriger als vor der Blutspende“.
Ein statistischer Test dient dazu, eine Entscheidung zwischen zwei Hypothesen zu treffen. Bevor wir kopfüber loslegen und eine Funktion anwenden, die uns das Ergebnis liefert, ist es wichtig, das Problem Schritt für Schritt zu stellen. Die Formulierung der Annahmen, die Wahl des statistischen Tests und die Analyse der Ergebnisse sind die wichtigsten Schritte. Wenn Sie mehr über statistische Tests erfahren möchten, gibt es in unserer Ausbildung zum Data Analyst und Data Scientist ein Modul, das diesem Thema gewidmet ist.









