Wenn du dich schon einmal für Methoden zur Dimensionsreduktion interessiert hast, hast du dich wahrscheinlich mit der Hauptkomponentenanalyse oder PCA beschäftigt. In diesem Artikel werden wir uns mit einer der anderen Methoden zur Dimensionsreduktion beschäftigen, die es gibt: t-SNE für t-distributed Stochastic Neighbor Embedding (t-distributed Stochastic Neighbor Embedding). Dieser Algorithmus bietet einen anderen Ansatz als die PCA.
t-SNE ist eine Technik zur Dimensionsreduktion, die bei der Erforschung großer Datenmengen eingesetzt wird. Sie wurde 2008 von Geoffrey Hinton und Laurens van der Maaten entwickelt. Wie bei der PCA besteht das Ziel darin, einen Raum mit kleinerer Dimension zu bestimmen, während die Abstände zwischen den Punkten erhalten bleiben.
Was ist der Unterschied zwischen t-SNE und PCA?
Die Hauptkomponentenanalyse ist eine weit verbreitete Methode zur Dimensionsreduktion, bei der versucht wird, die Daten in einer nahen Hyperebene so darzustellen, dass die Varianz der Datenwolke maximal erhalten bleibt. Mit anderen Worten: Die Daten werden in einem kleineren Unterraum dargestellt, der die gesamte Trägheit der Wolke, die in diesen Raum projiziert wird, maximiert. Wenn du mehr über die PCA wissen willst, schau dir unser Video dazu an:
Was ist das t-SNE-Prinzip?
Der t-SNE-Algorithmus besteht darin, eine Wahrscheinlichkeitsverteilung zu erstellen, die die Ähnlichkeiten zwischen Nachbarn in einem hochdimensionalen Raum und in einem kleineren Raum darstellt. Mit Ähnlichkeit wollen wir versuchen, Entfernungen in Wahrscheinlichkeiten umzuwandeln. Sie besteht aus drei Schritten:
- Schritt 1: Wir berechnen die Ähnlichkeiten der Punkte im großdimensionalen Ausgangsraum. Für jeden Punkt xi zentrieren wir eine Gaußsche Verteilung um diesen Punkt herum. Dann messen wir für jeden Punkt xj (i verschieden von j) die Dichte unter dieser zuvor definierten Gaußverteilung. Schließlich normalisieren wir für jeden Punkt. Wir erhalten eine Liste von bedingten Wahrscheinlichkeiten, die mit :
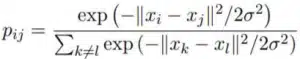
Die Standardabweichung wird anhand eines Wertes definiert, der Perplexität genannt wird und der Anzahl der Nachbarn um jeden Punkt entspricht. Dieser Wert wird vom User vorab festgelegt und dient dazu, die Standardabweichung der Gaußschen Verteilungen zu schätzen, die für jeden Punkt xi definiert sind. Je größer die Perplexität, desto größer ist die Varianz.
- Schritt 2: Wir müssen einen kleineren Raum erstellen, in dem wir unsere Daten darstellen. Natürlich kennen wir zu Beginn nicht die idealen Koordinaten auf diesem Raum. Daher werden wir die Punkte zufällig auf diesem neuen Raum verteilen. Der Rest ist ziemlich ähnlich wie in Schritt 1. Wir berechnen die Ähnlichkeiten der Punkte in dem neu erstellten Raum, allerdings unter Verwendung einer t-Student-Verteilung und nicht einer Gaußschen Verteilung. Auf die gleiche Weise erhalten wir eine Liste von Wahrscheinlichkeiten, die mit :
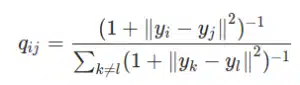
- Schritt 3: Um die Punkte im kleineren Raum genau darzustellen, möchten wir im Idealfall, dass die Ähnlichkeitsmaße in den beiden Räumen übereinstimmen. Daher müssen wir die Ähnlichkeiten der Punkte in den beiden Räumen mithilfe des Maßes Kullback_Leibler (KL) vergleichen. Wir versuchen dann, es durch Gradientenabstieg zu minimieren, um die bestmöglichen yi im kleinräumigen Raum zu erhalten. Dies ist gleichbedeutend mit der Minimierung der Abweichung der Wahrscheinlichkeitsverteilungen zwischen dem ursprünglichen Raum und dem Raum mit der kleinsten Dimension.
Wie unterscheiden sich die Methoden ACP und t-SNE?
Um die Unterschiede zwischen den beiden Methoden PCA und t-SNE besser zu verstehen, betrachten wir den MNIST-Datensatz. Für jede der beiden Methoden haben wir die Daten in einem zweidimensionalen Raum dargestellt.
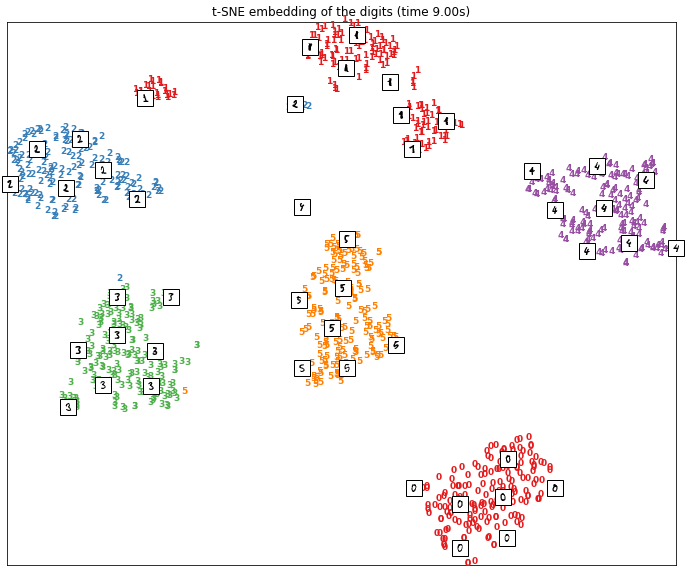
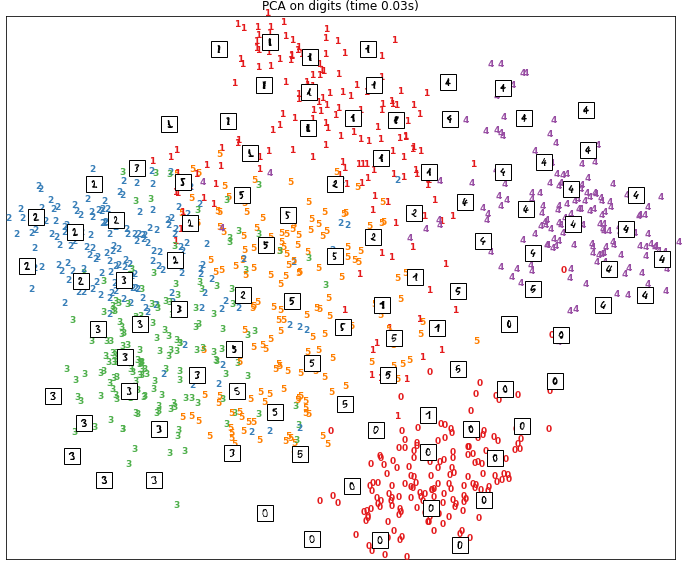
In der ersten Abbildung sehen wir das Ergebnis einer Dimensionsreduktion mit der t-SNE-Methode. In der zweiten Abbildung sehen wir das Ergebnis einer Hauptkomponentenanalyse.
Es ist klar, dass TSNE es geschafft hat, nahe beieinander liegende Daten zu gruppieren und unähnliche Daten voneinander zu entfernen. Die Punkte werden in Clustern dargestellt, wobei jeder Cluster einer Zahl zwischen 1 und 6 entspricht.
Bei den Ergebnissen der PCA ist die Trennung der Daten im zweidimensionalen Raum viel weniger deutlich. Wir können sehen, dass bei einigen Zahlen wie 0 die entsprechenden Punkte gut gruppiert sind. Bei anderen Zahlen, wie z. B. 5, sind die Punkte jedoch diffuser verteilt.
Wenn du dich über Themen wie Verkleinerungstechniken weiterbilden möchtest, dann besuche unsere Kurse im Bootcamp- oder im fortlaufenden Format!









