Die Graphentheorie ist ein Zweig der Mathematik und Informatik, bei dem verschiedene Probleme aus dem wirklichen Leben in Form von Graphen modelliert werden. Eine der klassischsten Anwendungen ist die Modellierung eines Straßennetzes zwischen verschiedenen Städten. Eines der Hauptprobleme ist die Optimierung der Entfernungen zwischen zwei Punkten. Um die kürzeste Strecke zu finden, wird oft der Dijkstra-Algorithmus verwendet. In diesem Artikel erfährst du mehr darüber, wie er funktioniert:
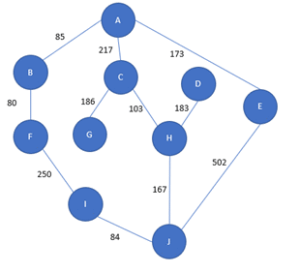
Hier werden die Städte A bis J durch die Eckpunkte des Graphen dargestellt.
Sie sind durch Straßen verbunden, die den Kanten des Graphen entsprechen. Jeder Kante ist ein Wert zugeordnet, der als Gewicht bezeichnet wird. Sie entspricht normalerweise den Kosten oder der Entfernung.
Hier kann jedes Gewicht als die Entfernung zwischen den beiden verbundenen Städten betrachtet werden.
Sehr schnell stellt sich ein Problem: Wie kann man den kürzesten Weg zwischen zwei Gipfeln bestimmen?
Hier kommt der Dijkstra-Algorithmus ins Spiel!
Wie funktioniert der Dijkstra-Algorithmus?
Angenommen, es wird versucht, den kürzesten Weg von Stadt A nach Stadt J zu finden.
Während des gesamten Algorithmus werden wir den kürzesten Weg von A zu jeder anderen Stadt in einer Tabelle speichern.
Immer wieder wird der gleiche Vorgang wiederholt:
- Du wählst den erreichbaren Gipfel mit der geringsten Entfernung als zu erforschenden Gipfel aus.
- Von diesem Gipfel aus erforscht man seine Nachbarn und aktualisiert die Entfernungen für jeden. Du aktualisierst die Distanz nur, wenn sie kleiner ist als die, die du vorher hattest.
- Dies wird so lange wiederholt, bis man am Zielpunkt angekommen ist oder bis alle Gipfel erkundet wurden.
Das ist alles ein bisschen vage…
Wie sieht das konkret aus?
Schlussfolgerung
Die abschließende Tabelle gibt uns den Wert des kürzesten Weges für jeden Eckpunkt des Graphen. Außerdem speichert sie den Ursprung des vorherigen Punktes, von dem aus der kürzeste Weg ermittelt wurde.
Zum Beispiel sagt uns der Wert 403C für den Gipfel G, dass es 403 km dauert, um ihn zu erreichen, und dass dieser kürzeste Weg direkt davor durch den Punkt C führt. Du kannst also einfach in der Tabelle nach oben scrollen, um den kürzesten Weg für jeden beliebigen Gipfel zu erhalten.
Diese Besonderheit erklärt den Vorteil des Dijkstra-Algorithmus: Mit nur einer Iteration erhält man den kürzesten Weg für jeden Gipfel!
Weiterführende Informationen:
- Es gibt viele andere Algorithmen, die das Problem des kürzesten Weges lösen. Man muss jedoch darauf achten, unter welchen Bedingungen diese verschiedenen Algorithmen angewendet werden. Der topologische Sortieralgorithmus zum Beispiel ist effizienter als der Dijkstra-Algorithmus, lässt sich aber nur auf azyklische Graphen (ohne Schleifen) anwenden.
- Die Komplexität des Dijkstra-Algorithmus ist polynomial. Sei n die Anzahl der Eckpunkte und a die Anzahl der Bögen, sie ist im schlimmsten Fall in O(a+ nlog(n))
- Edsger Dijkstra entdeckte diesen Algorithmus innerhalb von 20 Minuten, als er in einem Straßencafé nach dem besten Weg von Rotterdam nach Groningen suchte. Wie ein Kaffee viele Probleme lösen kann.
Hat dir dieser Artikel gefallen? Unser Data Scientist-Kurs beinhaltet auch einen Kurs über Graphentheorie. Warte nicht länger, sondern entdecke den Lehrplan!









