Wir behandeln ein neues Thema mit Daniel, dem technischen Support für die DataScientest-Schulungen. Der Experte für Data Science, der dich durch deine Schulung begleitet. Heute spricht er mit uns über Zeitreihen. Zeitreihen sind eines der am weitesten verbreiteten Studienobjekte der Datenwissenschaft. In diesem Artikel lernst du die Hauptkomponenten einer Zeitreihe kennen.
Was ist eine Zeitreihe?
Zeitreihen decken ein breites Spektrum an Phänomenen des realen Lebens ab und sind in vielen Bereichen anzutreffen.
Eine Zeitreihe kann die Bevölkerungsentwicklung oder das BIP eines Landes sein, ein Elektrokardiogramm oder der neueste Song von Dua Lipa.
Mathematisch gesehen ist eine Zeitreihe eine Reihe von Daten, die durch die Zeit indiziert sind.
Die Analyse und Vorhersage dieser Zeitreihen ist daher für bestimmte Industrien oder Wirtschaftszweige von größtem Interesse, denn konkret bedeutet die Vorhersage einer Zeitreihe die Vorhersage der Zukunft.
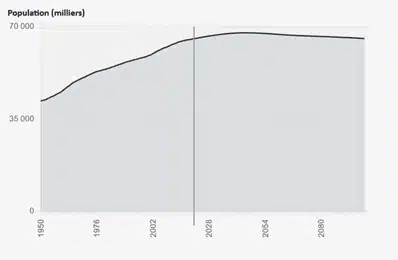
Wie zerfällt eine Zeitreihe?
Traditionell wird eine Zeitreihe in drei Elemente zerlegt:
- Ein Trend (Tt)
- Eine Saisonabhängigkeit (St)
- Ein Rest oder Fehler (εt)
Mathematisch kann man eine Zeitreihe also mit Xt = Tt + St + εt übersetzen.
Mit T der Trend, S die Saisonalität, ε das Residuum und t die Zeitindexierung.
Der Trend
Ein Trend ist ein zunehmendes oder abnehmendes Verhalten einer Reihe im Laufe der Zeit. Der Trend spiegelt häufig ein langfristiges Wachstums- oder Abnahmephänomen wider.
Der Trend in einer Zeitreihe kann verschiedene Formen annehmen:
- Linear Tt = α + βt
- Quadratisch Tt = α + βt + γt²
- Exponential Tt = α + βexp(t)
….
Saisonalität
Die Saisonalität spiegelt das Vorhandensein eines periodischen Phänomens wider, das sich entlang der Zeitreihe wiederholt.
Wenn sich also die saisonale Komponente in der Periode k wiederholt. St+k = St
Viele Daten sind saisonal bedingt, insbesondere Wetterdaten (Temperaturänderungen im Laufe der Zeit).
Einige Zeitreihen weisen sowohl einen Trend als auch eine Saisonalität auf, wie z. B. der weltweite Luftverkehr. Der Luftverkehr wächst, aber es gibt einen starken Unterschied zwischen dem Winter- und Sommerverkehr.
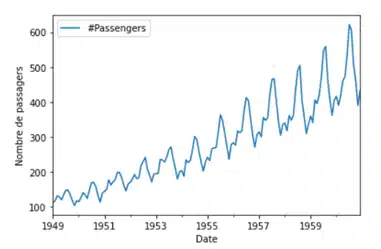
Der Rückstand
Das Residuum des Modells ist der Teil der Zeitreihe, der durch die Zerlegung nicht erklärt werden kann. Man kann eine Zeitreihe nicht vollständig nur nach Trend und Saisonalität zerlegen.
Im Idealfall ist das Residuum des Modells stationär, d.h. der verbleibende Prozess verändert sich nicht mit der Zeit (konstanter Mittelwert und konstante Varianz) . Wenn das Residuum unserer Zeitreihe nicht stationär ist, bedeutet dies, dass einige Zeitkomponenten im Modell nicht erklärt werden.
Sobald der Trend und die Saisonalität der Zeitreihe erklärt sind, kann man also versuchen, den Rest der Zerlegung mit Autoregressionsprozessen oder gleitenden Durchschnitten zu erklären, die das berühmte ARMA-Modell hervorgebracht haben.
Der Gral bei der Modellierung von Zeitreihen ist es, ein Residuum vom Typ des weißen Rauschens zu erhalten, d. h. ein Residuum, das keine Zeitinformationen mehr enthält. In der Praxis ist dies also ein zufälliges, unkorreliertes stationäres Signal.
Weiterführende Informationen
– Neben der Saisonalität wird manchmal auch ein Zyklus definiert, der als längerfristige Saisonalität angesehen werden kann, so dass mehrere verschiedene Zyklen definiert werden können.
– Das Vorhandensein einer nachgewiesenen Saisonalität zwischen zwei Zeitpunkten kann den Vergleich zwischen diesen Zeitpunkten erschweren. Je nach Fragestellung kann man daher versuchen, die saisonalen Schwankungen der Zeitreihen zu korrigieren. Dies ist z. B. bei der Arbeitslosenquote oder der Wachstumsrate der Fall, die von INSEE veröffentlicht werden.
– Die Zerlegung Xt = Tt + St + εt wird als additiv bezeichnet, man kann eine Zeitreihe auch nach einer multiplikativen Zerlegung Xt = Tt (1 + St )(1 + εt ) modellieren.
Schlussfolgerung
In diesem Artikel lernst du einige grundlegende Begriffe über Zeitreihen kennen: Trend, Saisonalität, Residuen, weißes Rauschen und Stationarität.
Neben den Zeitreihen umfasst die Datenwissenschaft jedoch auch viele andere Themen (Computer Vision, Natural Language Processing, Data Vizualisation, …), die du in einem unserer Data Scientist oder Data Engineer Kurse entdecken kannst.









