Was ist eine Wahrscheinlichkeit?
Eine Wahrscheinlichkeit quantifiziert die Chance bzw. das Risiko, dass ein Ereignis eintritt. Dieser Wert liegt immer zwischen 0 und 1.
Einige Anwendungsfälle der Wahrscheinlichkeit im Alltag
Das Werfen eines Würfels
Wenn man einen sechsseitigen ungesteppten Würfel wirft, hat man eine Chance von 1 zu 6, eine 3 zu würfeln.
Wir definieren das Ereignis A: „Es wird eine 3 gewürfelt“ und bezeichnen \mathbb{P}(A) als die Wahrscheinlichkeit dieses Ereignisses mit dem Wert: \mathbb{P}(A) = \frac{1}{6} Wir können weitere Ereignisse definieren, wie z. B. :
B: „Die gewürfelte Zahl ist ungerade“.
C: „Die Zahl ist größer oder gleich 5“.
Dann gilt: mathbb{P}(B) = \frac{3}{6} = \frac{1}{2} mathbb{P}(C) = \frac{2}{6} = \frac{1}{3} mathbb{P}(C) = \frac{2}{6} = \frac{1}{3}.
Wir können auch die Wahrscheinlichkeit berechnen, dass zwei Ereignisse zur gleichen Zeit eintreten.
[B \cap C [/latex]: „Die gewürfelte Zahl ist ungerade“ UND „Die gewürfelte Zahl ist größer oder gleich 5“.
Also ist B \cap C das Ereignis „Es wird eine 5 gewürfelt“.
Die Wahrscheinlichkeit, dass es eintritt, ist: mathbb{P}(B \cap C) = \frac{1}{6}.
Ebenso kann man die Wahrscheinlichkeit berechnen, dass mindestens eines von mehreren Ereignissen eintritt.
Das Ereignis D = B \cup C entspricht „Die gewürfelte Zahl ist ungerade“ ODER „Die gewürfelte Zahl ist größer oder gleich 5“, d. h. „Die gewürfelte Zahl ist 1, 3, 5 oder 6“.
In diesem Fall : \begin{aligned} \mathbb{P}(D) &= \mathbb{P}(B \cup C) \\ &= \mathbb{P}(B) + \mathbb{P}(C) – \mathbb{P}(B \cap C) \\&= \frac{1}{2} + \frac{1}{3} – \frac{1}{6} \\\mathbb{P}(D) &= \frac{2}{3} \\\end{aligned}
Ein Kartenstapel
Ein klassischer Kartenstapel besteht aus 52 Karten mit :
- 4 Farben (Pik, Karo, Kreuz, Herz)
- 13 Karten pro Farbe (von 2 bis 10, Bube, Dame, König, Ass)
On s’intéresse au résultat lorsqu’on tire une seule carte du paquet.
On définit les évènements :
- C : „La carte est un cœur“
- T : „La carte est une tête (valet, dame ou roi)“
- A : „La carte est un as“
Also:
- \mathbb{P}(C) = \frac{13}{52} = \frac{1}{4}
- \mathbb{P}(T) = \frac{12}{52} = \frac{3}{13}
- \mathbb{P}(A) = \frac{4}{52} = \frac{1}{13}
Wir erhalten auch:
- \mathbb{P}(T \cap C) = \frac{3}{52}
- \mathbb{P}(T \cap A) = 0
- \mathbb{P}(A \cap C) = \frac{1}{52}
Die Ergänzung zu diesen Ereignissen ist :
C^C: „Die Karte ist kein Herz“.
T^C: „Die Karte ist kein Kopf“.
A^C: „Die Karte ist kein Ass“.
In diesem Fall haben wir:
- \mathbb{P}(C^C) = 1 – \mathbb{P}(C) = 1 – \frac{1}{4} = \frac{3}{4}
- \mathbb{P}(T^C) = 1 – \mathbb{P}(T) = 1 – \frac{3}{13} = \frac{10}{13}
- \mathbb{P}(A^C) = 1 – \mathbb{P}(A) = 1 – \frac{1}{13} = \frac{12}{13}
Wenn wir eine Karte ziehen und wissen, dass es ein Herz ist, dann ist die Wahrscheinlichkeit, dass die Karte ein Kopf ist, frac{3}{13}.
Man spricht dann von bedingter Wahrscheinlichkeit: Es handelt sich um die Wahrscheinlichkeit unter der Bedingung einer bestimmten Information.
Man schreibt: \mathbb{P}(T | C) = \frac{mathbb{P}(T |cap C)}{mathbb{P}(C)}/.
Wir wissen, dass die Karte ein Herz ist. Es gibt insgesamt 13 Herzkarten, drei davon sind Köpfe, also haben wir eine Wahrscheinlichkeit von frac{3}{13}, dass wir einen Kopf gezogen haben, obwohl wir wissen, dass es ein Herz ist.
Berechnung :
\begin{aligned} \mathbb{P}(T | C) & = \frac{\mathbb{P}(T \cap C)}{\mathbb{P}(C)} \\ & = \frac{\frac{3}{52}}{\frac{1}{4}} \\ & = \frac{3}{13} \end{aligned}
Du bist an der Reihe
Wir verwenden einen Stapel mit 52 Karten.
- Wie hoch ist die Wahrscheinlichkeit, keine 8 zu ziehen?
- Wie hoch ist die Wahrscheinlichkeit, ein Ass oder ein Pik zu ziehen?
- Wie hoch ist die Wahrscheinlichkeit, einen König zu ziehen, wenn die gezogene Karte kein Kreuz ist?
Vokabeln und erste Eigenschaften
Wahrscheinlichkeitsraum
Wir befinden uns in einem Wahrscheinlichkeitsraum(\Omega, \mathcal{A}, \mathbb{P}) in dem :
\Omega das Univers ist
\mathcal{A} die Menge aller Ereignisse auf \Omega ist.
\mathbb{P} ist ein Wahrscheinlichkeitsmaß auf (\Omega,\mathcal{A})
Einige Eigenschaften
Gegeben sind A und B und zwei Vorfälle:
- \mathbb{P}(\emptyset)=0 et \mathbb{P}(\Omega)=1
- \mathbb{P}(A^C)= 1 – \mathbb{P}(A)
- \mathbb{P}(A \cup B)=\mathbb{P}(A) + \mathbb{P}(B) -\mathbb{P}(A \cap B)
Um diese letzte Gleichheit zu verstehen :
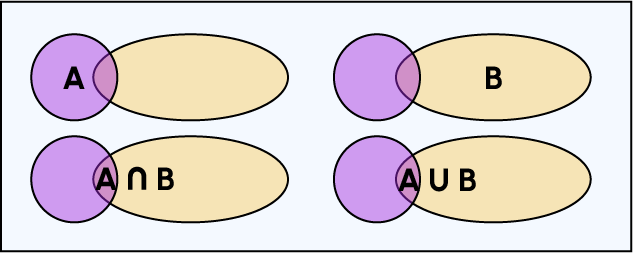
Bei der Berechnung der Wahrscheinlichkeit der Vereinigung zweier Mengen wird ein Teil entfernt, den man doppelt zählen könnte: der Schnittpunkt A, denn A ist in A enthalten und ist auch in B enthalten.
Umfassendes Ereignissystem
Ein vollständiges System von Ereignissen \left(E_i\right)_{i \in I} ist eine Menge von Teilen von\Omega, mit der I endlich oder abzählbar ist und erfüllt:
\bigcup\limits_{i \in I} E_i = \Omega
\forall \left(i,j\right) \in I^2, \quad i \ne j \Rightarrow E_i \cap E_j = \emptyset
Formel für die Gesamtwahrscheinlichkeit
Wir betrachten ein vollständiges System von Ereignissen \left(E_i\right)_{i \in I}.
Wir haben als Ereignis A, folgendes : \begin{aligned} \mathbb{P}\left(A\right) &= \sum \limits_{i \in I}{} \mathbb{P}\left(A \cap E_i\right) \\ &= \sum \limits_{i \in I}{} \mathbb{P}\left(A \vert E_i\right)\mathbb{P}\left(E_i\right) \\ \end{aligned}
Bedingungen
Wir betrachten einen Wahrscheinlichkeitsraum\left(\Omega, \mathcal{A}, \mathbb{P}\right).
Bedingte Wahrscheinlichkeit
Gegeben sei A \in \mathcal{A} ein Ereignis, so dass\mathbb{P}\left(A\right) \ne 0
Man nennt die bedingte Wahrscheinlichkeit A und notiert \mathbb{P}\left(\cdot\vert A \right) die Anwendung definiert auf\mathcal{A}
\forall B \in \mathcal{A} \quad \mathbb{P}\left(B \vert A\right) = \frac{\mathbb{P}\left(B \cap A\right)}{\mathbb{P}\left(A\right)}
Bayes'sches Theorem
Wir betrachten zwei Ereignisse A und B mit \mathbb{P}\left(B\right) \ne 0.
Dann gilt \mathbb{P}\left(A \vert B\right) = \frac{\mathbb{P}\left(B \vert A\right) \mathbb{P}\left(A\right)}{\mathbb{P}\left(B\right)}.
Beispiel
In einer Population sind 3 von 100 Personen von einer Krankheit betroffen.
Bei der Untersuchung auf diese Krankheit ist es möglich, dass der Test ein falsches Ergebnis liefert:
Wenn eine Person krank ist, besteht ein 2%-Risiko, dass der Test negativ ausfällt. Wenn eine Person nicht krank ist, besteht ein 0,5%-Risiko, dass der Test positiv ausfällt.
Frage
Wie hoch ist die Wahrscheinlichkeit, dass eine Person, deren Test positiv ausfällt, tatsächlich krank ist?
Antwort
Bezeichnen wir die Ereignisse:
M: Die Person ist krank.
T: Das Testergebnis ist positiv.
Dann kennen wir die folgenden Wahrscheinlichkeiten:
P(M)=3100P(M)=1003 (das ist die Wahrscheinlichkeit, dass eine Person krank ist)
P(TC∣M)=2100P(TC∣M)=1002 (das ist die Wahrscheinlichkeit, dass der Test einer kranken Person negativ ist)
P(T∣MC)=51000P(T∣MC)=10005 (das ist die Wahrscheinlichkeit, dass der Test einer gesunden Person positiv ist)
Dann kennen wir die folgenden Wahrscheinlichkeiten:
\mathbb{P}\left(M\right) = \frac{3}{100} (ist die Wahrscheinlichkeit, dass eine Person krank ist)
\mathbb{P}\left(T^C | M\right) = \frac{2}{100} (ist die Wahrscheinlichkeit, dass der Test einer kranken Person negativ ausfällt)
\mathbb{P}\left(T | M^C\right) = \frac{5}{1000} (ist die Wahrscheinlichkeit, dass der Test einer gesunden Person positiv ausfällt)
Das Problem ist, dass wir mathbbb{P}left(Tright) nicht kennen. Um diesen Wert zu berechnen, kann man die Formel für die Gesamtwahrscheinlichkeit verwenden. Dann bilden die Ereignisse T cap M und T cap M^C ein vollständiges System von Ereignissen in T. Die Formel für die Gesamtwahrscheinlichkeit ergibt :
\begin{aligned}\mathbb{P}\left(T\right) &= \mathbb{P}\left(T\cap M\right) + \mathbb{P}\left(T\cap M^C\right) \\ &= \mathbb{P}\left(T|M\right)\mathbb{P}\left(M\right) + \mathbb{P}\left(T|M^C\right)\mathbb{P}\left(M^C\right) \\ &= \left(1 – \mathbb{P}\left(T^C|M\right)\right)\mathbb{P}\left(M\right) + \mathbb{P}\left(T|M^C\right)\left(1 – \mathbb{P}\left(M\right)\right)\end{aligned}
Jetzt können wir berechnen: \mathbb{P}\left(M | T\right), da alle beteiligten Werte bekannt sind. \begin{aligned} \mathbb{P}\left(M | T\right) &= \frac{\left(1 – \mathbb{P}\left(T^C|M\right)\right)\mathbb{P}\left(M\right)}{\left(1 – \mathbb{P}\left(T^C|M\right)\right)\mathbb{P}\left(M\right) + \mathbb{P}\left(T|M^C\right)\left(1 – \mathbb{P}\left(M\right)\right)} \\ \\ &= \frac{\left(1 – \frac{2}{100}\right)\frac{3}{100}}{\left(1 – \frac{2}{100}\right)\frac{3}{100} + \frac{5}{1000}\left(1 – \frac{3}{100}\right)} \\ \\ &= \frac{588}{685} \\ \mathbb{P}\left(M | T\right) & \approx 85,84 \% \end{aligned}
Fazit
Das Ziel dieses Artikels war es, alle notwendigen Grundlagen der Wahrscheinlichkeitsrechnung zu vermitteln, um Teil 2 (der nicht allzu lange auf sich warten lassen sollte 😉) gut zu verstehen. Wahrscheinlichkeiten werden in mehreren Disziplinen sowie in vielen Machine-Learning- und Business-Intelligence-Tools umfassend genutzt. Die oben vorgestellten Konzepte sind Grundlagen, um die Funktionsweise dieser Werkzeuge mit einem besseren Verständnis einiger Algorithmen zu verstehen.
Außerdem sind Wahrscheinlichkeiten in Berufen, die mit Daten zu tun haben, sehr wichtig, insbesondere für Data Scientists und Analysten. DataScientest kann dir nicht nur helfen, deine Grundlagen zu erweitern, sondern dich auch bei deinem Kompetenzaufbau durch seine verschiedenen Kurse unterstützen. Besuche unsere Website oder kontaktiere uns direkt.









