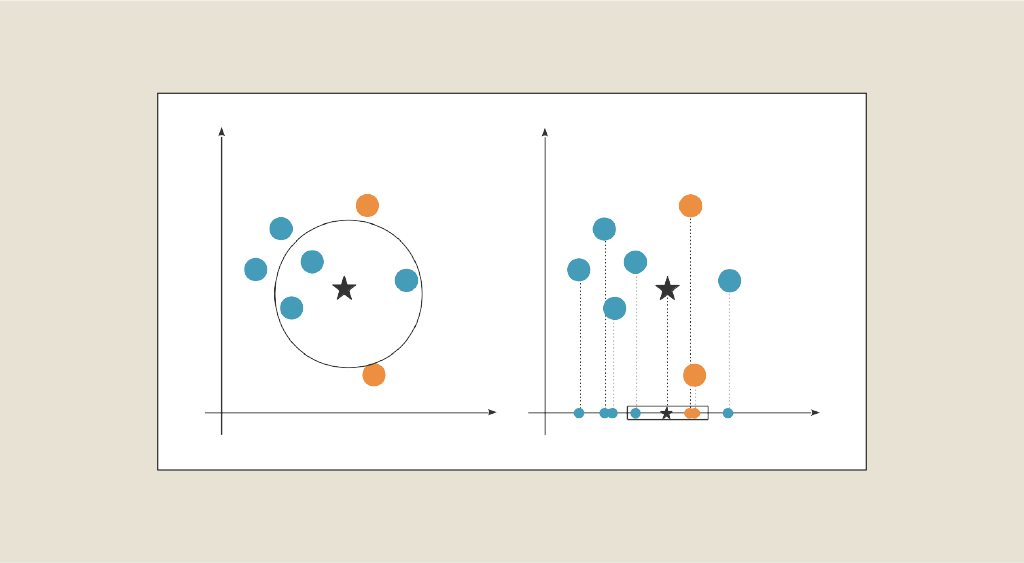
Die Datenanalyse kann als experimentelle Wissenschaft betrachtet werden, bei der Eigenschaften nach ihrer Beobachtung nachgewiesen werden und heuristisch Codes zur Interpretation der Ergebnisse erstellt werden. Im Bereich des maschinellen Lernens (Machine Learning) und der Datenanalyse spielt die Dimensionsreduktion eine wesentliche Rolle, um komplexe Datensätze zu vereinfachen.
Die Grundidee der Dimensionsreduktion besteht darin, mehrdimensionale Daten in einem Raum mit viel geringerer Dimension darzustellen, während wichtige und relevante Informationen erhalten bleiben.
Bevor wir uns in weitere mathematische Details vertiefen, ist es wichtig, einige Schlüsselbegriffe zu verstehen.
Das Vokabular der Dimensionsreduktion
Dimensionsraum: Die Anzahl der Merkmale oder Variablen, die ein Objekt in einem Datenbestand beschreiben. Eine Datenbank, die Merkmale über Personen sammelt, kann z. B. Variablen wie Alter, Einkommen, Adresse, Geschlecht und Bildungsniveau enthalten.
Dies definiert einen fünfdimensionalen Raum.
Bei der Projektion werden die Daten aus einem hochdimensionalen Raum mithilfe von Techniken zur Dimensionsreduktion in einen niedrigdimensionalen Raum umgewandelt. Durch diese Transformation können die Daten kompakter dargestellt werden, während wichtige Informationen erhalten bleiben.
Orthogonalität ist eine mathematische Eigenschaft, bei der zwei Vektoren oder zwei Räume senkrecht zueinander stehen. Im Zusammenhang mit der Dimensionsreduktion wird Orthogonalität häufig verwendet, um Variablen oder Komponenten zu beschreiben, die unkorreliert zueinander sind.
Wenn die Daten in einer Tabelle dargestellt werden, erfolgt die Verringerung der Dimensionalität durch eine Verringerung der Anzahl der Spalten. Wenn unser Dataset aus mehr als drei Variablen besteht, wird es mit zunehmender Dimension schwieriger, es zu visualisieren. So ist es nicht möglich, einen Datensatz mit 13 Attributen zu visualisieren, wohl aber mit nur 2 oder 3 Attributen. Das Ziel ist also, diese Daten auf die 2 oder 3 Achsen zu projizieren, die für den Informationsgehalt am wichtigsten sind, um die Darstellung der Daten so nah wie möglich an den Daten in großen Dimensionen zu halten.
Ein sehr einfaches Beispiel: Angenommen, wir haben einen Datensatz mit Informationen über Schüler, der die folgenden 5 Variablen enthält, und jeder Schüler wird durch eine Zeile im Datensatz repräsentiert, wobei jede Variable einer Spalte entspricht.
| Student | Alter | Grösse | Gewicht | Mathe | Wissenschaft |
|---|---|---|---|---|---|
| Etudiant 1 | 18 | 165 | 60 | 85 | 90 |
| Etudiant 2 | 20 | 170 | 65 | 75 | 80 |
| Etudiant 3 | 19 | 175 | 70 | 90 | 95 |
| Etudiant 4 | 22 | 180 | 75 | 80 | 70 |
Nach Anwendung der Hauptkomponentenanalyse zur Reduzierung der Dimension könnten wir einen neuen Datensatz mit weniger Variablen erhalten, z. B. indem wir nur die ersten beiden Hauptkomponenten beibehalten. Wir würden den folgenden Datensatz erhalten:
| Student | Hauptkomponente 1 | Hauptkomponente 2 |
|---|---|---|
| Student 1 | 0.23 | -0.12 |
| Student 2 | -0.12 | 0.10 |
| Student 3 | 0.30 | 0.25 |
| Student 4 | -0.41 | -0.23 |
So lässt sich dieser Datensatz leicht in einem zweidimensionalen Diagramm darstellen:

Mehr über die Hauptkomponentenanalyse (Principal Component Analysis, PCA)
Eine der am häufigsten verwendeten Methoden ist die Hauptkomponentenanalyse (Principal Component Analysis, PCA). Die PCA versucht, die Hauptrichtungen der Daten zu finden, die den größten Teil der beobachteten Varianz erklären. Dazu verwenden wir den Begriff der Kovarianz.
Stellen wir unseren Datensatz, der aus n Beobachtungen (Stichproben) und p Variablen (Merkmalen) besteht, durch eine Matrix X der Größe n x p dar. Vor der Anwendung der PCA wird oft empfohlen, die Variablen so zu standardisieren, dass sie einen Mittelwert von Null und eine Einheitsvarianz haben, damit Variablen mit unterschiedlichen Skalen die Analyse nicht dominieren.
Wir berechnen die Kovarianzmatrix von X, die wir mit C bezeichnen. Diese Matrix misst die linearen Beziehungen zwischen den Variablen. Sie wird mit der folgenden Formel berechnet: C = 1/nXT X
Wir suchen nach den Eigenvektoren der Kovarianzmatrix C. Eigenvektoren sind Richtungen im Raum der Variablen, die die Varianz der Daten beschreiben. Die Eigenvektoren werden normalisiert, so dass ihre Norm 1 ist.
Wir ordnen diese Eigenvektoren in absteigender Reihenfolge ihres zugehörigen Eigenwerts an: ν1 in Verbindung mit λ1, ν2 in Verbindung mit λ2 und λ1≥λ2 und so weiter. Je höher der Eigenwert, desto größer ist die Varianz, die durch die entsprechende Richtung erklärt wird.
Man wählt eine Anzahl k von Hauptkomponenten (oft 1, 2 oder 3), die man behalten möchte, und wählt die ersten k Eigenvektoren (ν1, ν2, … , νk) aus. Diese Eigenvektoren bilden eine Orthonormalbasis in dem neuen Raum mit reduzierter Dimension. Somit sind die neu erzeugten Variablen unkorreliert. Wir bezeichnen W als die Matrix, die von diesen ersten k Eigenvektoren gebildet wird.
Wir wollen nun unsere Daten in diesen neuen Raum projizieren, dessen eine Basis aus den Vektoren (ν1, ν2, … , νk) besteht. Um die Originaldaten in diesen Raum mit reduzierter Dimension zu projizieren, verwenden wir die folgende lineare Transformation: Y = XW, wobei Y den Koordinaten unserer Daten infolge der Projektion entspricht.
Für weitere Details über die PCA kannst du unseren Artikel lesen, der speziell dieser Methode gewidmet ist.
Es gibt noch andere Methoden zur Dimensionsreduktion, die bekanntesten sind nach wie vor :
- LDA (linear discriminant analysis): Die lineare Diskriminanzanalyse, die es ermöglicht, voneinander unkorrelierte Richtungen zu identifizieren. Sie zielt darauf ab, eine lineare Projektion der Daten zu finden, die die Trennung zwischen den Klassen maximiert und gleichzeitig die Varianz innerhalb der Klassen minimiert.
- T-SNE (t-Distributed Stochastic Neighbor Embedding): T-SNE ist eine nichtlineare Methode zur Dimensionsreduktion, mit der hochdimensionale Daten in einem Raum mit reduzierter Dimension (typischerweise 2D oder 3D) dargestellt werden können. Weitere Details zu diesem Thema findest du in diesem Artikel. t-NSE ist besonders geeignet, um komplexe Strukturen und nichtlineare Beziehungen in den Daten zu visualisieren.
Grenzen und Schwierigkeiten der Verkleinerung
Es ist wichtig zu beachten, dass die Verkleinerung der Dimension einen Kompromiss zwischen der Vereinfachung der Daten und dem Verlust von Informationen darstellt. Bei einer Verkleinerung der Dimension können einige subtile Informationen oder spezifische Details verloren gehen. Daher ist es entscheidend, das richtige Gleichgewicht zu finden, indem man eine angemessene Anzahl von Hauptkomponenten auswählt, die den Großteil der relevanten Informationen erfassen.
Jede Methode hat ihre Vorteile und Grenzen, und die Wahl der Methode hängt vom spezifischen Kontext und den Zielen der Datenanalyse ab.
Wenn dir dieser Artikel gefallen hat, kannst du diese Methoden in unseren Kursen Data Analyst und Data Scientist genauer kennen lernen. Du kannst sie dir gerne ansehen!