Kennst du die PCA? Diese Methode ist sehr nützlich und wird bei Dimensionsreduktionen verwendet. Erfahre in diesem Artikel, wie sie funktioniert.
Wer hat nicht schon einmal einen Datensatz mit einer sehr großen Anzahl von Variablen in den Händen gehalten, ohne zu wissen, welche die wichtigsten sind? Wie kann man diesen Datensatz so reduzieren, dass er auf einfache Weise auf 2 oder 3 Achsen dargestellt werden kann? Hier kommt die PCA!
Die Hauptkomponentenanalyse ist die Antwort auf diese Fragen. Die PCA ist eine bekannte Methode zur Dimensionsreduktion, mit der hoch korrelierte Variablen in neue, unkorrelierte Variablen umgewandelt werden können.
Das Prinzip ist einfach: Es geht darum, die Informationen, die in einer großen Datenbank enthalten sind, in einer Reihe von synthetischen Variablen zusammenzufassen, die als Hauptkomponenten bezeichnet werden.
Die Idee ist dann, diese Daten auf die nächstgelegene Hyperebene zu projizieren, um eine einfache Darstellung unserer Daten zu erhalten.
Natürlich bedeutet eine Verkleinerung der Dimension einen Verlust an Informationen. Das ist die Herausforderung bei der Hauptkomponentenanalyse. Du musst in der Lage sein, deine Daten zu verkleinern und gleichzeitig ein Maximum an Informationen zu erhalten.
Wie funktioniert eine Hauptkomponentenanalyse?
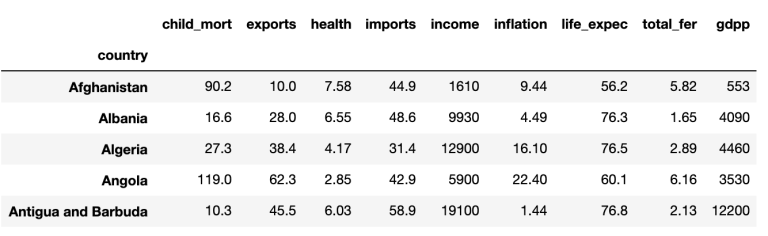
Um das Prinzip der PCA zu veranschaulichen, nehmen wir als Beispiel einen Datensatz mit dem Namen ‚country_data‚, der, wie der Name schon sagt, mehrere Informationen (BIP; Durchschnittseinkommen; Lebenserwartung; Geburten-/Mortalitätsrate etc.) über verschiedene Länder zusammenfasst.
Hier sind die ersten fünf Zeilen:
Anschließend ist es wichtig, unsere Variablen zu zentrieren und zu reduzieren, um den Skaleneffekt abzuschwächen, da sie nicht auf derselben Basis berechnet werden.
Wenn du diesen Schritt gemacht hast, musst du unsere Daten als eine Matrix aus
von der wir Eigenwerte und Eigenvektoren berechnen werden.
In der linearen Algebra entspricht der Begriff des Eigenvektors der Untersuchung von Vorzugsachsen, nach denen sich eine Anwendung eines Raumes in sich selbst wie eine Dilatation verhält, wobei die Vektoren mit einer Konstante multipliziert werden, die Eigenwert genannt wird. Die Vektoren, auf die das zutrifft, heißen Eigenvektoren, die in einem Eigenraum zusammengefasst sind.
Nach dem Importieren des PCA-Moduls von sklearn.decomposition werden folgende Eigenwerte zurückgegeben
Die Eigenwerte sind:[3.48753851 1.47902877 1.15061758 0.93557048 0.65529084 0.15140052].
Mithilfe dieser Eigenwerte können wir die optimale Anzahl an Hauptfaktoren/Komponenten für unsere PCA bestimmen. Wenn die optimale Anzahl der Komponenten beispielsweise 2 ist, dann werden unsere Daten auf zwei Achsen dargestellt und so weiter.
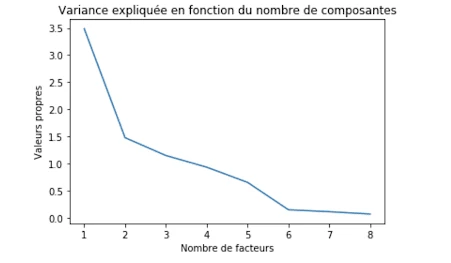
In diesem Diagramm, das die Anzahl der zu wählenden Faktoren in Abhängigkeit von den Eigenwerten darstellt, zeigen wir, dass die optimale Faktorwahl 2 beträgt (dank der Knickmethode). Wir werden also von einer Dimension 9 zu einer Dimension 2 übergehen, was die Basisdimension erheblich reduziert. Wie bereits erwähnt, wird es durch diese Reduzierung zwangsläufig zu einem Informationsverlust kommen. Dennoch bleibt eine Informationsrate von fast 70 % erhalten, was uns erlaubt, eine Darstellung zu erhalten, die meiner 9-dimensionalen Darstellung nahe kommt.
Nachdem das PCA-Modul die Koordinaten unserer Daten berechnet hat, müssen wir sie nur noch darstellen, aber bevor wir das tun, werden wir uns mit einem Werkzeug beschäftigen, das sehr oft verwendet wird, wenn man eine Hauptkomponentenanalyse durchführt, nämlich dem Korrelationskreis.

Da unsere Darstellung auf zwei Achsen beruht, ist der Korrelationskreis ein praktisches Hilfsmittel, mit dem wir die Bedeutung jeder erklärenden Variable für jede Achse der Darstellung visualisieren können. Die Richtung jedes Pfeils zeigt an, welche Achse durch die Variable erklärt wird, und die Richtung zeigt an, ob die Korrelation positiv oder negativ ist. Es fällt auf, dass Variablen wie „income„, „gdpp“ und „health“ positiv mit der ersten Achse korreliert sind, während „child_mort“ oder „total_fer“ zwar auch positiv, aber negativ korreliert sind. Wir können uns nun ansehen, wie die Länder auf den beiden Achsen der PCA dargestellt werden und welchen Einfluss die Variable „life_expec“ auf ihre Darstellung hat.
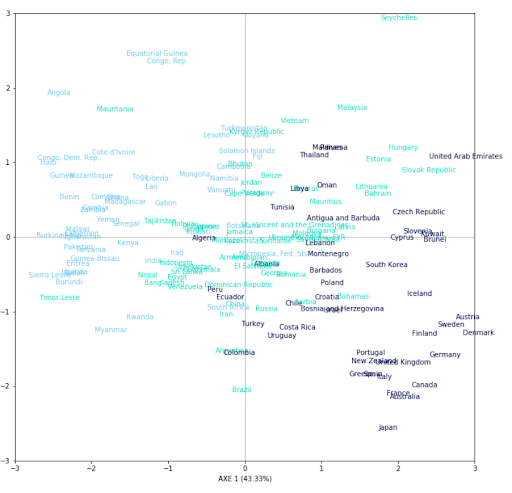
Hier ist eine Darstellung jedes Landes (167) auf 2 Achsen. Um die Qualität unserer Darstellung zu beurteilen, haben wir beschlossen, jedes Land entsprechend seiner Lebenserwartung in drei Gruppen einzufärben, wobei wir eine gewisse Tendenz erkennen können. Wir können feststellen, dass die Länder mit einer hohen Lebenserwartung im unteren rechten Teil des Diagramms konzentriert sind. Der Korrelationskreis zeigt, dass die Personen in diesem Bereich teilweise durch die Variablen „health„, „income“ oder „gdpp“ erklärt werden. Daraus lässt sich schließen, dass die Länder, die am meisten für Gesundheit ausgeben, eine höhere Lebenserwartung haben. Dasselbe gilt für die Länder, die sich im oberen linken Teil des Diagramms befinden. Der Korrelationskreis zeigt, dass dieser Teil am meisten durch die Variablen „child_mort“ oder „total_fer“ erklärt wird.
Wenn du mehr über die Hauptkomponentenanalyse oder andere Methoden zur Reduzierung von Dimensionen erfahren möchtest, gibt es in unserer Data Analyst-Weiterbildung mehrere Module, die sich damit beschäftigen.