Markov Modelle verstehen: Man sagt, dass ein Modell die Markov-Eigenschaft besitzt, wenn sein Zustand zu einem Zeitpunkt T nur von seinem Zustand zum Zeitpunkt T-1 abhängt. Wenn man die Zustände, in denen sich das Modell zu jedem Zeitpunkt befindet, beobachten kann, spricht man von einem beobachtbaren Markov-Modell. Andernfalls spricht man von einem Hidden-Markov-Modell.
In diesem Artikel werden wir diese Modelle veranschaulichen, um zu verstehen, wie sie funktionieren und wie nützlich sie sind.
Beobachtbares Markov-Modell
Betrachte die folgende Situation:
Du bist an einem regnerischen Tag zu Hause eingesperrt und möchtest das Wetter für die nächsten fünf Tage bestimmen.
Da Du kein Meteorologe bist, machst Du es Dir einfach, indem du annimmst, dass das Wetter einem Markov-Modell folgt: Das Wetter am Tag T hängt nur vom Wetter am Tag T-1 ab.
Um die Sache noch weiter zu vereinfachen, nimmst du an, dass es nur drei mögliche Wettervarianten gibt:
- Sonne
- Wolken
- oder Regen.
Basierend auf den Beobachtungen der letzten Monate erstellst Du das folgende Übergangsdiagramm:
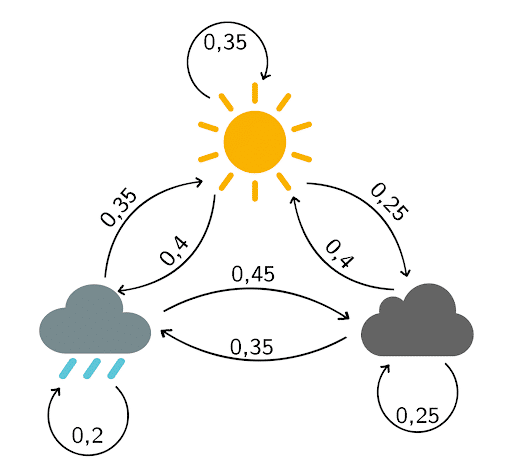
Die zugehörige Übergangsmatrix lautet:
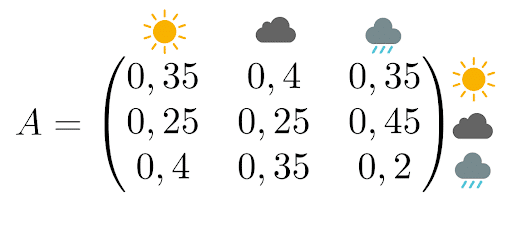
Zur Erläuterung: Diese Matrix liest sich wie folgt:
- Die Wahrscheinlichkeit, dass es morgen sonnig wird, wenn man weiß, dass es heute regnet, beträgt 35 %.
- Die Wahrscheinlichkeit, dass es morgen bewölkt ist, beträgt 25 %, wenn man bedenkt, dass es heute schon bewölkt ist.
Berechnen wir die Wahrscheinlichkeit, dass das Wetter in den nächsten fünf Tagen „Sonne, Sonne, Regen, Wolken, Sonne“ sein wird.
Da das Wetter an einem Tag nur vom Wetter am Vortag abhängt, multipliziere einfach die Wahrscheinlichkeiten (zur Erinnerung: heute regnet es):
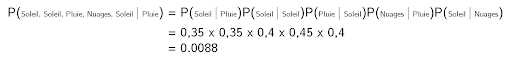
Man kann diese Wahrscheinlichkeit für alle möglichen Kombinationen berechnen und die Kombination mit der höchsten Wahrscheinlichkeit auswählen, um die Fragestellung zu beantworten.
In unserem Fall sind dies die fünf Kombinationen, die am wahrscheinlichsten eintreten (Nuage = Wolken, Soleil= Sonne, Pluie = Regen, Prob. = Warsch.)

Hidden-Markov-Modell
Wir behalten die gleichen Annahmen wie im vorherigen Teil bei.
Nehmen wir nun an, dass ein Wetterpsychopath dich in einen fensterlosen Raum gesperrt hat, in dem nur ein Computer und eine Lampe stehen. Jeden Tag leuchtet die Lampe in einer bestimmten Farbe, je nachdem, wie das Wetter ist. Dein Entführer stellt dir die folgende Beobachtungsmatrix zur Verfügung:
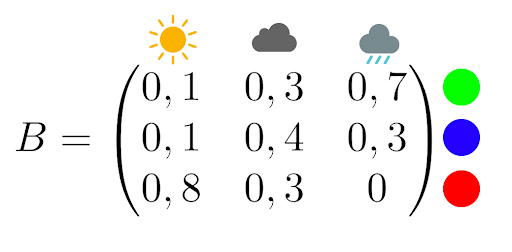
Wenn es z. B. regnet, ist die Lampe mit 70 % Wahrscheinlichkeit grün und mit 30 % Wahrscheinlichkeit blau.
Du kannst nach Hause gehen, wenn du das Wetter für die nächsten fünf Tage nur anhand der Farbe der Lampe bestimmst. Du baust dann ein Hidden-Markov-Modell.
Du bleibst fünf Tage lang eingesperrt und stellst die folgenden Farben fest:
blau, blau, rot, grün, rot.
Du erinnerst dich daran, dass es am Tag vor deinem Einschluss geregnet hat.
Du kannst nun einen Python-Code schreiben, der die Kombination zurückgibt, die mit der höchsten Wahrscheinlichkeit eintritt:
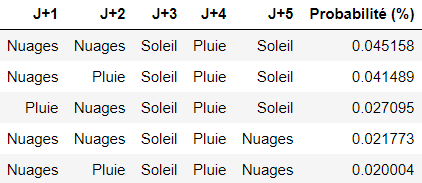
NB: Man hätte auch den Viterbi-Algorithmus implementieren können, der die wahrscheinlichste Kombination zurückgibt, also [‚Wolken‘, ‚Wolken‘, ‚Sonne‘, ‚Regen‘, ‚Sonne‘].
Dieser Ansatz zur Vorhersage ist interessant, aber sehr grob. Wenn du lernen möchtest, beeindruckendere Vorhersagen zu treffen, z. B. mithilfe von Machine-Learning-Algorithmen, dann kontaktiere uns direkt online, um weitere Informationen über unsere Kurse in Data Science zu erhalten!