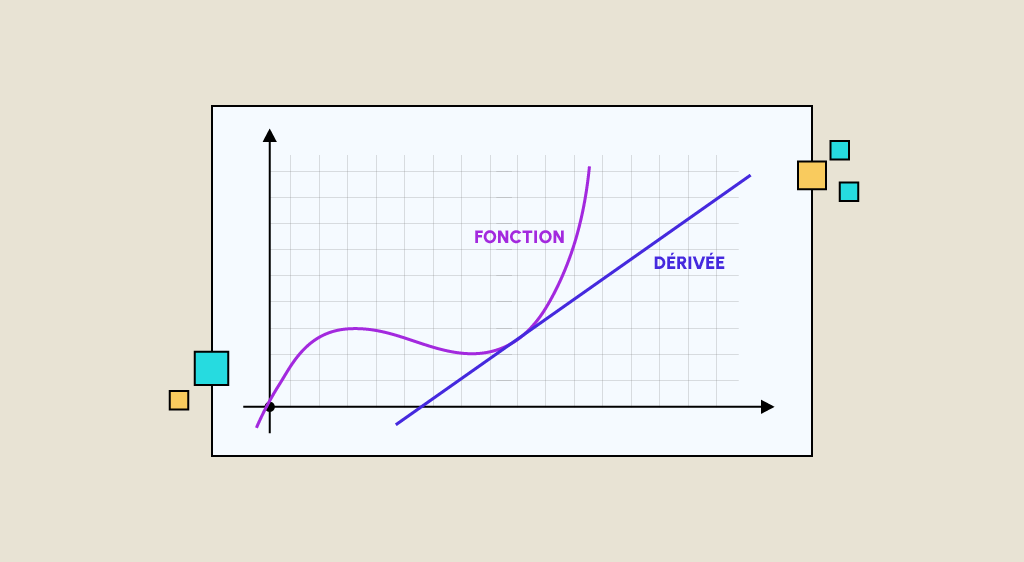
Der Begriff der Ableitung wird insbesondere in der DataScience sehr häufig verwendet, um Modelle für das maschinelle Lernen zu erlernen. Abgesehen von dem, was Du wahrscheinlich in der Schule gesehen hast, sind die Anwendungen dieses mathematischen Werkzeugs viel breiter gefächert, und wir werden am Ende dieses Artikels darauf zurückkommen. In diesem Artikel erfährst Du zunächst, wie Du die Ableitung einer Funktion berechnen kannst, und anschließend gehen wir etwas näher auf den Nutzen dieser Berechnung ein.
Definition
Der Begriff der Ableitung ist n. Die Ableitung einer Funktion f(x) stellt die Änderungsrate dieser Funktion dar. Sie kann auch als f'(x) oder dfdx bezeichnet werden. Die Berechnung und Untersuchung der Ableitung ist ein wichtiger Bestandteil des Studiums von Funktionen und wird vor allem in der DataScience für das Lernen von Machine-Learning-Modellen verwendet. Abgesehen von dem, was Du wahrscheinlich in der Schule gesehen hast, sind die Anwendungen dieses mathematischen Werkzeugs viel breiter gefächert, und wir werden am Ende dieses Artikels darauf zurückkommen.
In diesem Artikel erfährst Du zunächst, wie Du die Ableitung einer Funktion berechnen kannst, und anschließend gehen wir etwas näher auf den Nutzen dieser Berechnung ein.
Formeln
Die Berechnung einer Ableitung ist im Allgemeinen recht einfach, wenn man die grundlegenden Formeln der üblichen Funktionen kennt.
Diese Formeln sind in der folgenden Tabelle zusammengefasst:
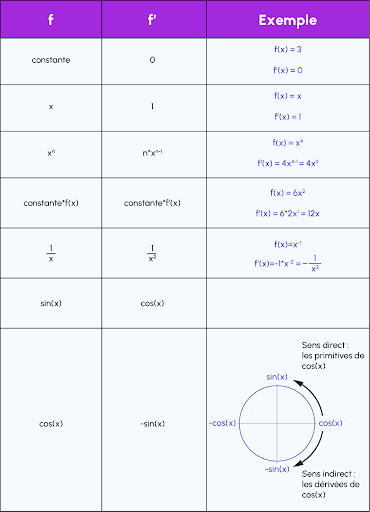
Mit dieser Tabelle kannst du dir die grundlegendsten Ableitungen anzeigen lassen.
Ableitung – Summe der Funktionen
Wenn deine Funktion die Summe von mehreren anderen Funktionen ist :
f(x)=u(x)+v(x)
dann ist ihre Ableitung die Summe der Ableitungen:
f'(x)=u'(x)+v'(x).
Zum Beispiel:
f(x)=x2+3
In diesem Fall ist u(x)=x2 und v(x)=3.
Wir können also berechnen
u'(x)=(x2)’=2×2-1=2x
v'(x)=(3)‘ = 0
f'(x)=u'(x)+v'(x) = 2x + 0 = 2x.
Ableitung – Produkte von Funktionen
Für die Multiplikation von Funktionen:
f(x)=u(x)*v(x)
Die totale Ableitung ist etwas spezieller und entspricht der folgenden Regel:
f'(x)=u'(x)*v(x)+u(x)*v'(x)
f(x)=x2sin(x)
In diesem Fall ist u(x)=x2 und v(x)=sin(x).
Wir können also berechnen
u'(x)=(x2)’=2×2-1=2x
v'(x)=(sin(x))‘ = cos(x)
f'(x)=u'(x)*v(x)+u(x)*v'(x) = 2x*sin(x) + x2*cos(x)
Quotienten von Funktionen
Wenn eine Funktion die Division von zwei anderen Funktionen ist: f(x)=u(x)v(x), dann wird die Ableitung wie folgt aussehen
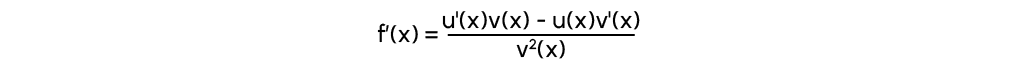
Beispiel:
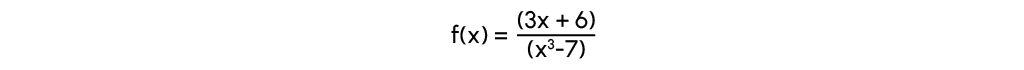
In diesem Fall ist u(x)=(3x+6) und v(x)=(x3-7).
Wir können also berechnen:
u'(x)=(3x+6)’=3
v'(x)=(x3-7)‘ =3×2
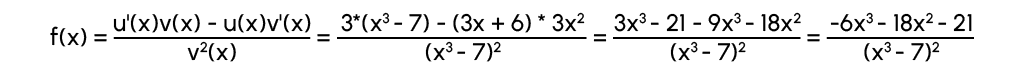
Zusammengesetzte Funktionen
Wenn Deine Funktion als zwei zusammengefasste Funktionen oder, anders ausgedrückt, als Funktion einer Funktion wahrgenommen wird :
h(x)=f(g(x))=f ◦ g.
dann wird seine Ableitung von auf diese Weise berechnet:
h'(x)=(f ◦ g) ‚ = g‘ .(f ‚ ◦ g).
Beispiel:

Wir können also Folgendes annehmen:
g(x)=x2+2x-4 und g'(x)=2x+2
f(x)=x und f'(x)=121×1/2=12x

Und

Also

Anwendungen
Mais à quoi sert vraiment le calcul de la dérivée ?
Pour faire simple, le signe de la dérivée permet d’indiquer les variations de la fonction f. C’est ce qui représente la tangente à la fonction
Aber wozu dient die Berechnung der Ableitung wirklich?
Vereinfacht gesagt, kann man anhand des Vorzeichens der Ableitung die Variationen der Funktion f erkennen.
Es stellt die Tangente an die Funktion dar. Und die Ableitung selbst stellt den Leitkoeffizienten der Tangente an f im Punkt dar.
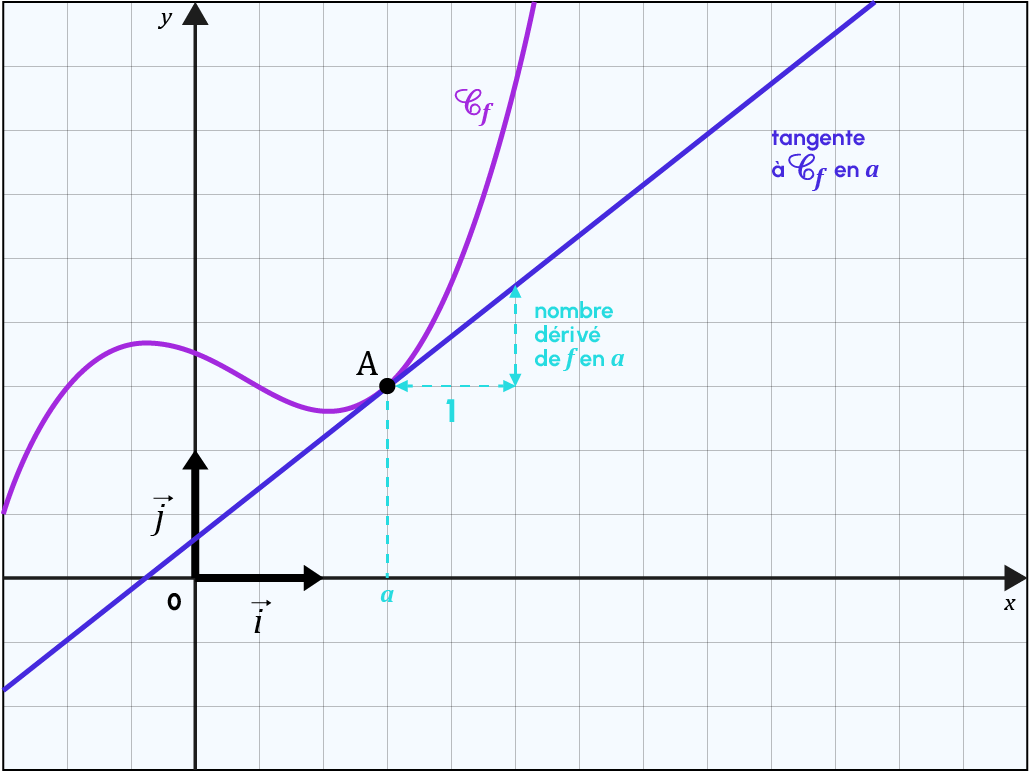
Zur Erinnerung: Die Tangente einer Funktion in einem Punkt ist die Gerade, die die Funktion in diesem Punkt und nur in diesem Punkt berührt.
Wenn f ‚ ≥ 0, dann ist f steigend.
Wenn f ‚ ≤ 0, dann ist f abnehmend.
Und wenn f’=0, haben wir den Punkt x, an dem der Leitkoeffizient der Tangente annulliert wird und die Funktion f möglicherweise ihre Variation ändert.
Zum Beispiel:
f(x)=x2-4x+2
f'(x)=2x-4
f'(x)=0 ⇔ 2x=4 ⇔ x=2
Dies deutet also darauf hin, dass fürx=2 meine Funktion vielleicht ihre Variation ändert. Wie du unten sehen kannst, stellt x=2 einen Wendepunkt dar:
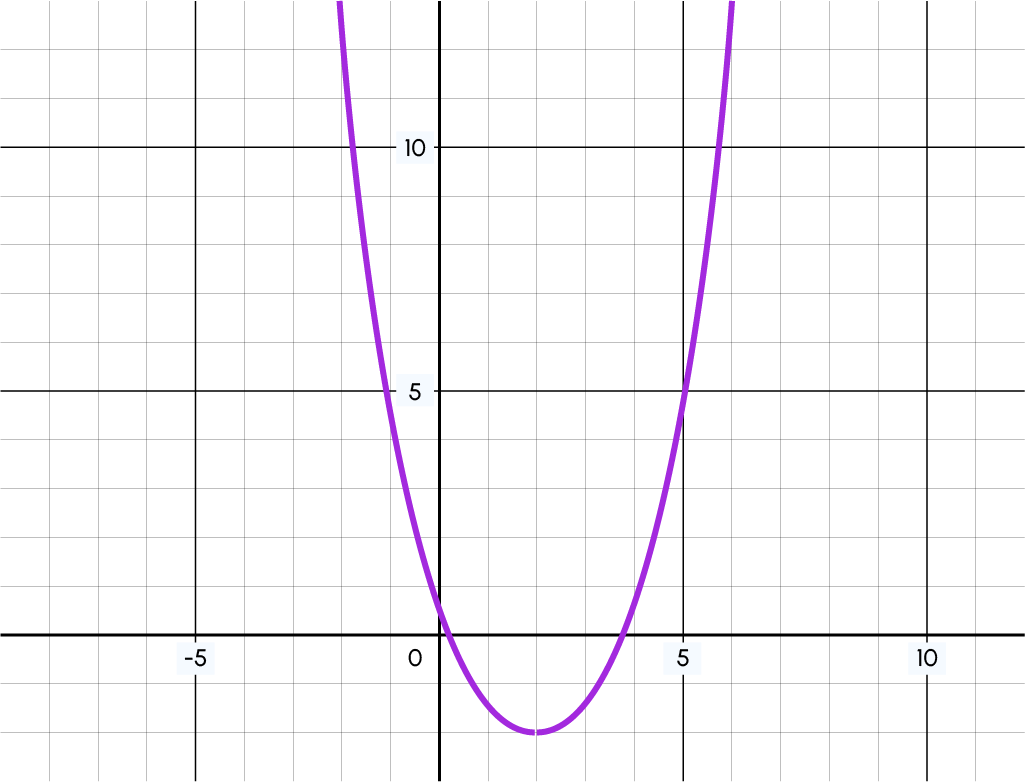
Wenn du also x durch x<2 ersetzt, z. B. x=1,
Wir haben:
f'(1)=2 × 1-4=⎯2<0
Die Ableitung ist kleiner als 0, also nimmt die Funktion f ab.
Wenn wir x durch x>2 ersetzen, z. B. x=3,
Wir haben:
f'(3)=2*3-4=2>0
Die Ableitung ist größer als 0, also wächst die Funktion f.
Wir haben also die folgende Variationstabelle:
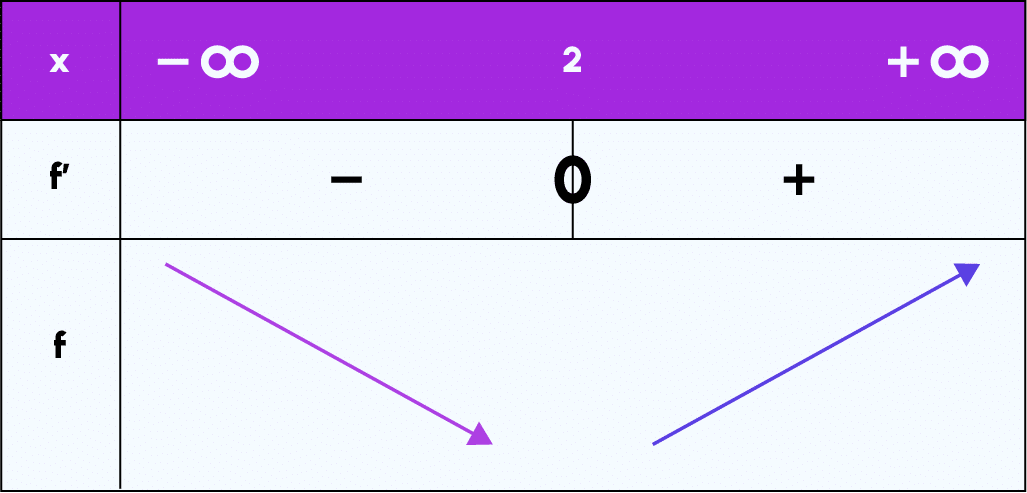
Aber was ist nun die Verbindung zum maschinellen Lernen?
In Machine-Learning-Problemen versuchen wir, das Minimum der Kostenfunktion zu finden, um den Fehler in der Vorhersage zu minimieren und so die Leistung des Modells zu maximieren.
Um dies zu erreichen, suchen wir das Minimum der Funktion mithilfe der Ableitung.
Die Berechnung der Ableitung und ihre Gleichsetzung mit 0, um die entsprechenden x zu finden, führt jedoch nicht mit Sicherheit zu analytischen Lösungen.
Aus diesem Grund verwenden wir die Methode des Gradientenabstiegs.