Korrelation ist ein statistisches Werkzeug, das für Machine Learning verwendet wird, um Abhängigkeitsbeziehungen zwischen mehreren Variablen zu identifizieren. Es gibt verschiedene Arten von Korrelationen. Erfahre unten mehr über die Pearson- und die Spearman-Korrelation.
Für die Datenanalyse stehen einem Data Scientist verschiedene statistische Werkzeuge zur Verfügung. Unter diesen Werkzeugen kann er die Korrelation verwenden. Dies ist ein besonders nützliches statistisches Maß, mit dem die Beziehung zwischen zwei Variablen anhand der Berechnung eines Korrelationskoeffizienten untersucht werden kann.
Die Korrelation entspricht der Stärke (angegeben durch den absoluten Wert des Koeffizienten) und der Richtung (angegeben durch das Vorzeichen des Koeffizienten) der Beziehung zwischen diesen Variablen. Die Richtung kann entweder positiv (wenn ein x steigt, steigt auch y) oder negativ (wenn x steigt, sinkt y oder umgekehrt) sein.
Es gibt verschiedene Arten von Korrelationen. Unter diesen Korrelationen gibt es zwei, die besonders häufig verwendet werden: Die Pearson vs. Spearman Korrelation. Diese beiden Arten von Korrelationen werden im weiteren Verlauf dieses Artikels näher erläutert.
Pearson vs. Spearman Korrelation - Was ist Pearson?
Die Pearson-Korrelation, auch lineare Korrelation genannt, misst den linearen Zusammenhang zwischen zwei kontinuierlichen Variablen. Die Pearson-Korrelation wird durch den Wert des Korrelationskoeffizienten r angegeben, der mithilfe der folgenden Formel berechnet wird:

Bevor du den Pearson-Koeffizienten berechnest, musst du sicherstellen, dass die Daten die folgenden Annahmen erfüllen:
- Die Datenstichprobe ist zufällig (repräsentativ für die Grundgesamtheit).
- Die Variablen sind quantitativ (kontinuierlich).
- Die Daten sind paarweise verknüpft (jedem Wert x wird ein Wert y zugeordnet).
- Die Beobachtungen sind unabhängig
- Die Daten sind normalverteilt
- Es besteht eine lineare Beziehung zwischen den Variablen.
- Es gibt keine Ausreißer in den Daten
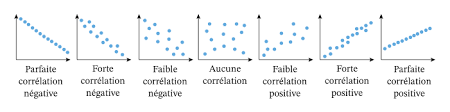
Der Wert des Korrelationskoeffizienten r liegt zwischen -1 und 1. Je nach dem Wert von r gibt es mehrere mögliche Fälle:
- Wenn r nahe bei 1 liegt, dann sind die Variablen linear positiv voneinander abhängig.
- Wenn r nahe bei 0 liegt, dann gibt es keine lineare Beziehung zwischen den Variablen.
- Wenn r nahe bei -1 liegt, dann sind die Variablen linear negativ abhängig.
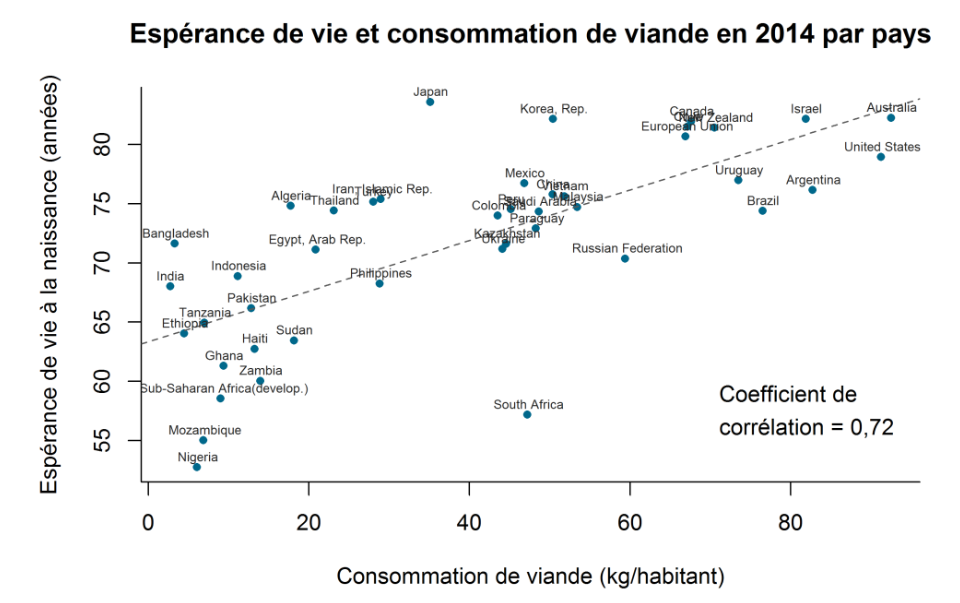
Ein Beispiel für die Anwendung der Pearson-Korrelation wäre z. B. die Untersuchung des Zusammenhangs zwischen Fleischkonsum und Lebenserwartung in verschiedenen Ländern.
Pearson vs. Spearman Korrelation - Was ist Spearman?
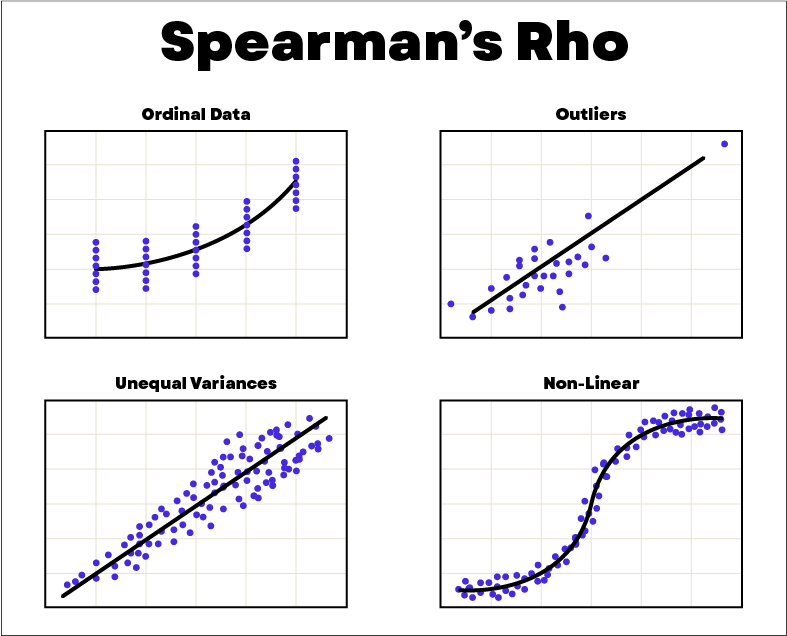
Die Spearman-Korrelation ist ein Korrelationsmaß, das eine monotone Beziehung zwischen zwei Variablen anhand des Datenrangs misst. Ein Beispiel für die Bestimmung des Datenrangs ist: [58,70,40] wird zu [2,1,3].
Die Spearman-Korrelation wird häufig für Daten verwendet, die aus Ausreißern bestehen. Um die Spearman-Korrelation zu messen, wird als Indikator der Spearman-Koeffizient rs verwendet, der auch als Rangkoeffizient bezeichnet wird und in der folgenden Formel angegeben ist. In dieser Formel gibt die Variable n die Anzahl der Punkte in der Datenreihe an. Die Variable d ist das Quadrat der Differenz der Ränge zwischen jedem Punkt mit den Koordinaten (x,y).
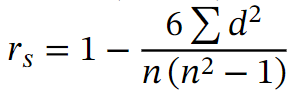
Bevor du den Spearman-Koeffizienten berechnest, musst du sicherstellen, dass die Daten die folgenden Annahmen erfüllen:
- Die Stichprobe der Daten ist zufällig.
Die Beziehung zwischen den Variablen ist monoton - Die Daten sind paarweise verknüpft
- Die Beobachtungen sind unabhängig
- Es besteht eine monotone Beziehung zwischen den Variablen.
- Die Variablen sind ordinal oder stetig.
Die Interpretation des Spearman-Koeffizienten rs variiert je nach den erhaltenen Werten:
- Wenn rs nahe bei 1 liegt, dann gibt es eine positive monotone Beziehung zwischen den Variablen.
- Wenn rs nahe 0 ist, dann gibt es keine monotone Beziehung zwischen den Variablen.
- Wenn rs nahe bei -1 liegt, dann gibt es eine negative monotone Beziehung zwischen den Variablen.
Ein Beispiel für die Anwendung der Spearman-Korrelation wäre die Untersuchung der Beziehung zwischen den Präferenzen eines Verbrauchers und dem Preis eines Produkts.
Fazit
Die Spearman vs. Pearson Korrelation sind zwei verschiedene Korrelationsmaße, die in bestimmten Situationen Anwendung finden. Die Spearman-Korrelation verwendet den Rang der Daten, um die Monotonie zwischen ordinalen oder kontinuierlichen Variablen zu messen. Die Pearson-Korrelation hingegen erkennt lineare Beziehungen zwischen quantitativen Variablen mit Daten, die einer Normalverteilung folgen. Bei Problemen mit Machine Learning werden oft Korrelationsmatrizen verwendet, die aus den Korrelationskoeffizienten zwischen allen Variablen in einem Datensatz bestehen. Der Begriff der Korrelation ist also wichtig für Machine Learning.
Wenn du dich in Machine Learning weiterbilden lassen möchtest, um tiefer in den Bereich der Datenwissenschaft einzusteigen, dann schau dir unsere Weiterbildungen zum Data Scientist und Data Analyst an.