Clustering ist eine spezielle Disziplin von Machine Learning, mit dem Ziel, deine Daten in homogene Gruppen mit gemeinsamen Merkmalen aufzuteilen. Dies ist z. B. ein beliebtes Gebiet im Marketing, wo oft versucht wird, Kundenstämme zu segmentieren, um bestimmte Verhaltensweisen zu erkennen. Der K-Mittelwert-Algorithmus (K-means) ist ein sehr bekannter unüberwachter Algorithmus für das Clustering.
In diesem Artikel werden wir detailliert beschreiben, wie es funktioniert und welche nützlichen Mittel es gibt, um es zu optimieren.
Dieser Algorithmus wurde 1957 in den Bell Laboratorien von Stuart P. Lloyd als Pulscodemodulations-Technik (PCM) entwickelt. Er wurde erst 1982 der breiten Öffentlichkeit vorgestellt. Im Jahr 1965 hatte Edward W. Forgy einen fast ähnlichen Algorithmus veröffentlicht, weshalb K-Means oft als Lloyd-Forgy-Algorithmus bezeichnet wird.
Die Anwendungsbereiche sind vielfältig: Kundensegmentierung, Datenanalyse, Segmentierung eines Bildes, semi-überwachtes Lernen…
Das Prinzip des k-means-Algorithmus
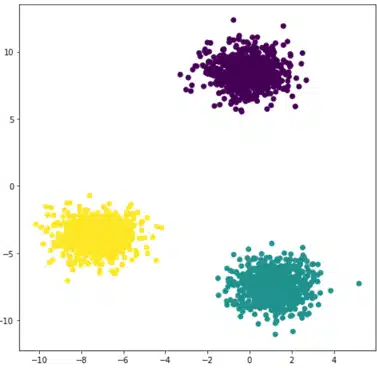
Wenn Punkte und eine ganze Zahl k gegeben sind, zielt der Algorithmus darauf ab, die Punkte in k homogene und kompakte Gruppen, sogenannte Cluster, zu unterteilen. Schauen wir uns das folgende Beispiel an:
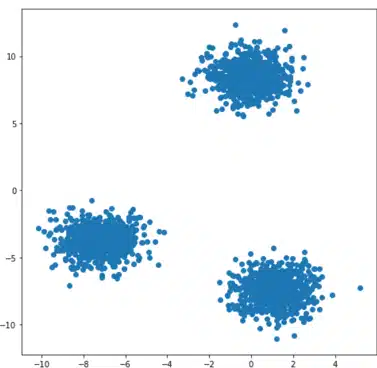
Wie geht man konkret vor?
Die Idee ist ziemlich einfach und intuitiv. Der erste Schritt besteht darin, drei Zentroiden zufällig zu definieren, denen wir drei Bezeichnungen zuordnen, z. B. 0, 1, 2. Dann schauen wir uns für jeden Punkt die Entfernung zu den drei Zentroiden an und verbinden den Punkt mit dem nächstgelegenen Zentroiden und dem entsprechenden Label. Dies entspricht einer Beschriftung unserer Daten.
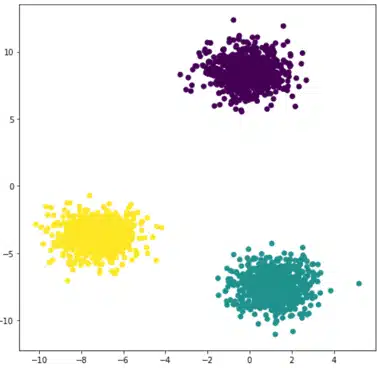
Schließlich berechnen wir drei neue Zentroiden, die die Schwerpunkte jeder beschrifteten Punktwolke sein werden. Diese Schritte werden so lange wiederholt, bis die neuen Zentroide sich nicht mehr von den vorherigen unterscheiden. Das Endergebnis ist in der Abbildung rechts zu sehen.
Begriff der Entfernung und Initialisierung
In diesem Algorithmus sind zwei Punkte entscheidend: Welche Metrik wird verwendet, um die Entfernung zwischen den Punkten und den Zentroiden zu bewerten? Wie viele Cluster müssen ausgewählt werden? Im k-Mittelwert-Algorithmus wird normalerweise die euklidische Distanz verwendet, d.h. p = (p1,….,pn) und q = (q1,….,qn).
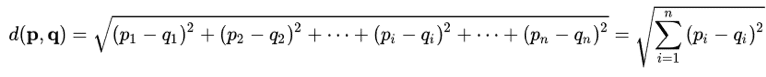
Sie ermöglicht es, die Entfernung zwischen jedem Punkt und den Zentroiden zu schätzen. Für jeden Punkt wird die euklidische Distanz zwischen diesem Punkt und jedem Zentroiden berechnet und dann dem nächstgelegenen Zentroiden zugeordnet, d.h. demjenigen mit der geringsten Distanz.
Im vorherigen Beispiel war es einfach, die ideale Anzahl von Clustern zu finden, indem man sie grafisch darstellte. Normalerweise haben Datensätze mehr als zwei Dimensionen und es ist daher schwierig, die Punktwolke zu visualisieren und die optimale Anzahl von Clustern schnell zu identifizieren. Nehmen wir im vorherigen Beispiel an, dass wir die Daten nicht vorher visualisiert haben und beschließen, verschiedene Male mit einer unterschiedlichen Anzahl an anfänglichen Clustern zu testen. Hier sind die erhaltenen Ergebnisse:
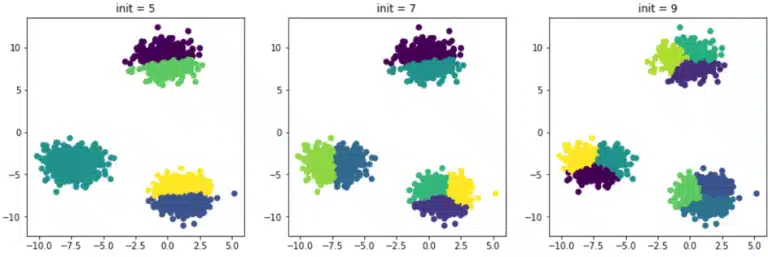
Die Partitionierung ist ungenau, da die Anzahl der anfänglichen Cluster viel höher ist als die ideale Anzahl, in diesem Fall 3. Es gibt Methoden, um die ideale Anzahl von Clustern zu bestimmen. Die bekannteste ist die Ellbogenmethode. Sie stützt sich auf den Begriff der Trägheit.
Diese wird wie folgt definiert: die Summe der euklidischen Abstände zwischen jedem Punkt und seinem zugehörigen Zentroid. Je höher die anfängliche Anzahl der Cluster ist, desto geringer ist die Trägheit: Die Punkte haben eine größere Chance, neben einem Zentroid zu liegen. Schauen wir uns an, wie das in unserem Beispiel aussieht:
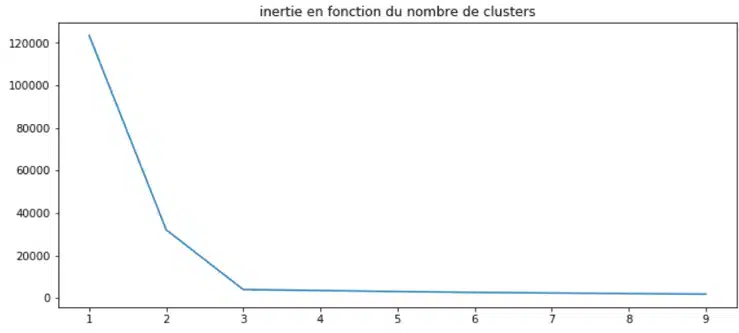
Es fällt auf, dass die Trägheit ab 3 Clustern stagniert. Diese Methode ist schlüssig. Man kann sie mit einem präziseren Ansatz verbinden, der jedoch mehr Rechenzeit erfordert: dem Silhouettenkoeffizienten. Er wird wie folgt definiert:
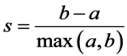
- a der durchschnittliche Abstand zu anderen Beobachtungen im selben Cluster (cad der Durchschnitt innerhalb des Clusters).
- b die durchschnittliche Entfernung zum nächstgelegenen Cluster.
Dieser Koeffizient kann zwischen -1 und +1 variieren. Ein Koeffizient nahe +1 bedeutet, dass die Beobachtung gut innerhalb ihres eigenen Clusters liegt, während ein Koeffizient nahe 0 bedeutet, dass sie nahe einer Grenze liegt; schließlich bedeutet ein Koeffizient nahe -1, dass die Beobachtung mit dem falschen Cluster in Verbindung gebracht wird.
Wie bei der Trägheit ist es sinnvoll, die Entwicklung des Koeffizienten in Abhängigkeit von der Anzahl der Cluster wie folgt anzuzeigen:
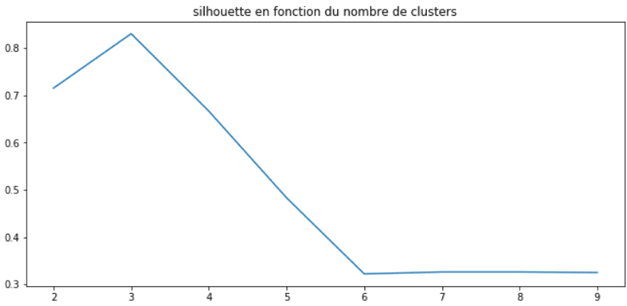
Diese Methode hilft auch dabei, die ideale Anzahl von Clustern zu finden, d.h. 3. Zusätzlich zu diesen beiden Methoden ist es wichtig, eine gründliche Analyse der erstellten Cluster durchzuführen. Darunter verstehe ich eine genaue und gründliche beschreibende Analyse, um die gemeinsamen Merkmale jedes Clusters zu bestimmen. Dies wird dir helfen, die typischen Profile jedes Clusters zu verstehen.
Und nun die Praxis in Python
Das Workout eines K-Mittelwert-Algorithmus wird durch die Bibliothek Sci-Learning erleichtert Scikit-Learn. Unser Beispieldatensatz lässt sich leicht mit der Funktion make_blobs von Scikit-Learn erstellen. Hier ist, wie sie in Code implementiert wird:

Jetzt, da wir unseren Datensatz haben, können wir mit der Implementierung eines K-means weitermachen. Wir benutzen die Scikit-Learn Bibliothek und sehen uns das Ergebnis an:
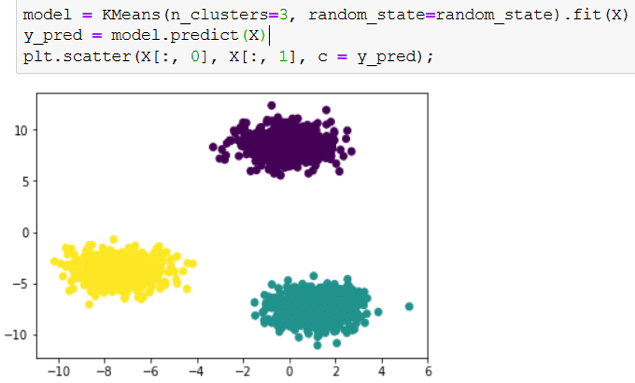
Das Attribut n_clusters der KMeans-Klasse von Scikit-Learn ermöglicht es, die Anzahl der gewünschten Zentroiden festzulegen. Daher legt es auch die Anzahl der anfänglichen Zentroiden fest. Diese Klasse verwendet standardmäßig keine zufällige Initialisierungsmethode, sondern eine Methode, die 2007 von David Arthur und Sergei Vassilvitskii entwickelt wurde und K-MEANS ++ heißt. Bei dieser Methode werden Zentroide ausgewählt, die sich voneinander unterscheiden, wodurch das Risiko einer Konvergenz zu einer nicht-optimalen Lösung verringert wird. Die Standarddistanz ist natürlich die oben definierte euklidische Distanz.
Wo liegen die Grenzen des k-means-Algorithmus?
Wie wir gesehen haben, muss der Algorithmus zunächst die Anzahl der Partitionen festlegen. Dies erfordert eine genaue Vorstellung davon, und obwohl wir zwei komplementäre Methoden zur Optimierung für bestimmte Datensätze gesehen haben, sind sie nicht unfehlbar.
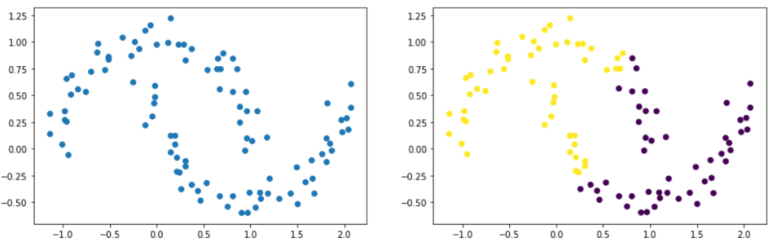
Das liegt daran, dass Datensätze mit z. B. elliptischen Formen problematisch sein können. Im folgenden Beispiel siehst du deutlich zwei Gruppen, die zwei Ellipsen ähneln. Die rechte Abbildung zeigt das Ergebnis nach der Anwendung des k-Mittelwert-Algorithmus. Es ist klar, dass der Algorithmus nicht in der Lage war, unsere beiden Ellipsen zu identifizieren.
Bei Datascientest lernst du, die wichtigsten Clustering-Algorithmen zu beherrschen und sie in Datensätzen zu interpretieren.
Erkunde unsere Kursangebote und bewirb dich für einen Kurs, um mehr über Clustering, aber auch über viele andere Bereiche des Machine Learning zu erfahren.