Word Embedding bezeichnet eine Reihe von Lernmethoden, die darauf abzielen, Wörter in einem Text durch Vektoren reeller Zahlen darzustellen. Heute präsentieren wir dir den dritten Teil unseres NLP-Dossiers.
Hast du die ersten Episoden verpasst? Keine Sorge, hier sind sie:
Dieser Abschnitt soll die Funktionsweise erklären und den berühmten Word2vec-Algorithmus in Python implementieren.
Word Embedding
Zur Erinnerung: Word Embedding ist in der Lage, den Kontext, die semantische und syntaktische Ähnlichkeit (Genus, Synonyme, …) eines Wortes zu erfassen, indem es die Dimensionen verringert.
Man könnte z. B. erwarten, dass die Wörter „bemerkenswert“ und „bewundernswert“ durch Vektoren dargestellt werden, die in dem Vektorraum, in dem diese Vektoren definiert sind, relativ wenig voneinander entfernt sind.
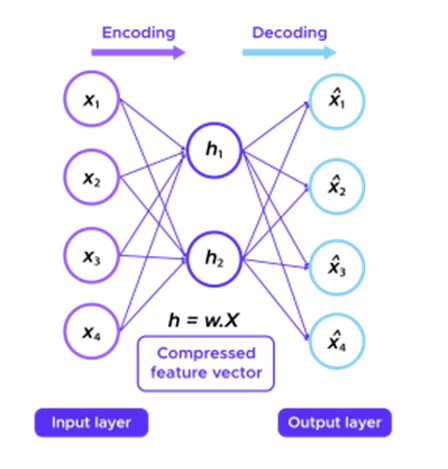
Die allgemein verwendete Einbettungsmethode, um die Größe eines Vektors zu reduzieren, besteht darin, das Ergebnis zu verwenden, das eine dichte Schicht zurückgibt, d. h. eine Einbettungsmatrix W mit der „one hot“-Darstellung des Wortes zu multiplizieren:

In Vektorform :
Embedding mit Word2vec
Um die Einschränkungen der ersten Methode zu vermeiden, ist es jedoch möglich, die W-Matrix mithilfe des bekannten Word2Vec-Algorithmus unüberwacht mit einfachem Text zu trainieren.
Wie funktioniert Word2vec?
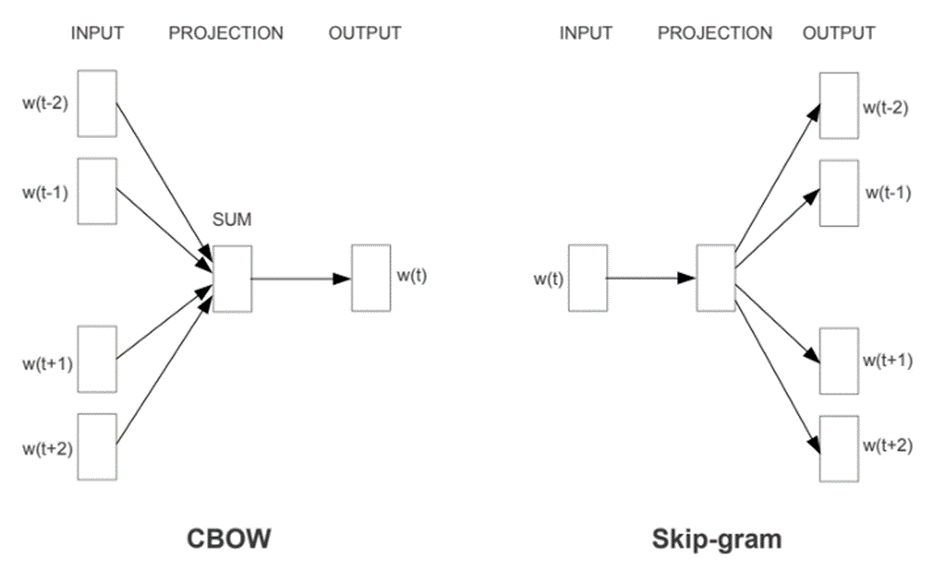
Es gibt zwei Varianten des Word2vec, beide verwenden ein neuronales Netz mit drei Schichten (1 Eingabeschicht, 1 verborgene Schicht, 1 Ausgabeschicht): Common Bag Of Words (CBOW) und Skip-gram.
In der folgenden Abbildung wird das Wort im blauen Feld als Zielwort bezeichnet und die Wörter in den weißen Feldern werden als Kontextwörter in einem Fenster der Größe 5 bezeichnet.

CBOW: Das Modell wird mit dem Kontext gefüttert und sagt das Zielwort voraus. Das Ergebnis der verborgenen Schicht ist die neue Repräsentation des Wortes (ℎ1, …, ℎ𝑁).
Skip Gram: Das Modell wird mit dem Zielwort gefüttert und sagt die Wörter im Kontext voraus. Das Ergebnis der verborgenen Schicht ist die neue Darstellung des Wortes (ℎ1, …, ℎ𝑁).
Formatierung der Daten:
Hier werden wir das CBOW-Modell vorstellen, d. h. der Kontext ist der Input unseres Modells und das Zielwort (blaues Wort) ist der Output. Wir definieren ein Fenster mit der Länge 5 für den Kontext (Eingabe).


Modell:
Das CBOW-Modell hat Ähnlichkeiten mit dem Klassifikationsmodell, das wir gerade im vorherigen Abschnitt implementiert haben. Unser Modell wird aus den folgenden Schichten bestehen:
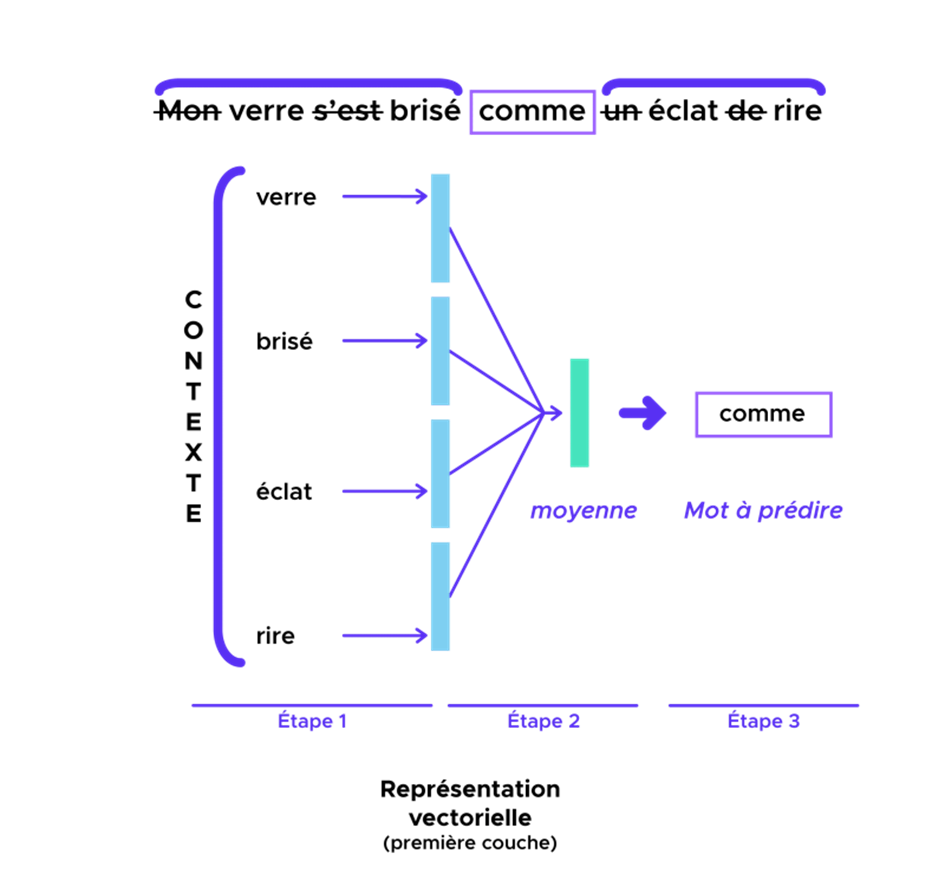
- Die Embedding-Schicht wird jedes Wort im Kontext in einen Embedding-Vektor umwandeln. Die W-Matrix des Embeddings wird im Laufe des Workouts des Modells erlernt. Die resultierenden Dimensionen sind: (lot, context_size, embedding).
- Anschließend können mit der GlobalAveragePooling1D-Schicht die verschiedenen Einbettungen summiert werden, um eine Ausgabegröße zu erhalten (batch_size, embedding).
- Schließlich kann der Dense-Layer mit der Größe „voc_size“ das Zielwort vorhersagen.
Die Cross-Entropy-Loss-Funktion wird in der Regel zum Workout des Modells :
Metrisch in diesem Raum:
Da das Modell nun trainiert ist, kann es interessant sein, den Abstand zwischen den Wörtern zu vergleichen.
Die „Cosine similarity“ wird im Allgemeinen als Metrik zur Messung der Entfernung verwendet, wenn die Norm der Vektoren keine Rolle spielt. Diese Metrik erfasst die Ähnlichkeit zwischen zwei Wörtern.
Je näher die „cosine similarity“ an 1 liegt, desto mehr sind die beiden Wörter miteinander verwandt.
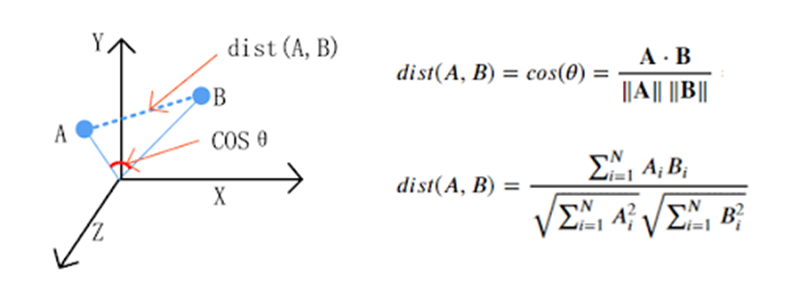
Mit dieser Metrik und in diesem Untervektorraum sind die 5 Wörter, die am nächsten an „body“ liegen, :
intestines - 0.30548161268234253
bodies - 0.2691531181335449
arm - 0.24878980219364166
chest - 0.2261650413274765
leg - 0.2193179428577423
Die obigen Zahlen stellen die Cos-similar-Distanzen zwischen dem Wort „body“ und den nächstliegenden Wörtern dar.
Zum Wort „Zombie„:
Slasher - 0.3172745406627655
cannibal - 0.28496912121772766
zombies - 0.2767203450202942
horror - 0.2607246935367584
zombi - 0.25878411531448364
Zum Wort „amazing„:
glänzend - 0.3372475802898407
extraordinary - 0.319326251745224
great - 0.29579296708106995
breathtaking - 0.2907085716724396
fantastic - 0.2871546149253845
Zum Wort „god„:
heavens - 0.268303781747818
jesus - 0.26807624101638794
goodness - 0.2618488669395447
gods - 0.24795521795749664
doom - 0.22242328524589539
Arithmetische Eigenschaften:
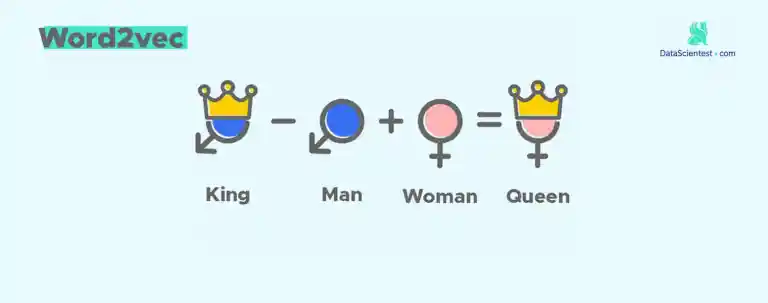
Wir können uns nun die Frage stellen, ob unser Untervektorraum der Wörter arithmetische Eigenschaften hat. Nehmen wir das folgende berühmte Beispiel:
𝐾𝑖𝑛𝑔 – 𝑀𝑎𝑛 + 𝑊𝑜𝑚𝑎𝑛 = 𝑄𝑢𝑒𝑒𝑛
In diesem Beispiel ist die arithmetische Eigenschaft das Königtum. Wir möchten überprüfen, ob sich diese Eigenschaft auf „woman“ ausbreiten wird. Das heißt, wir werden nach den Wörtern suchen, die dem folgenden Vektor am nächsten liegen:
arithmetic_vector = word2vec[index_word1] – word2vec[index_word2] + word2vec [index_word3].
Hier ist das Wort „queen“ in unserem Datensatz nicht sehr stark vertreten, was eine schlechte Darstellung erklärt. Aus diesem Grund werden wir uns stattdessen mit der Zahleneigenschaft :
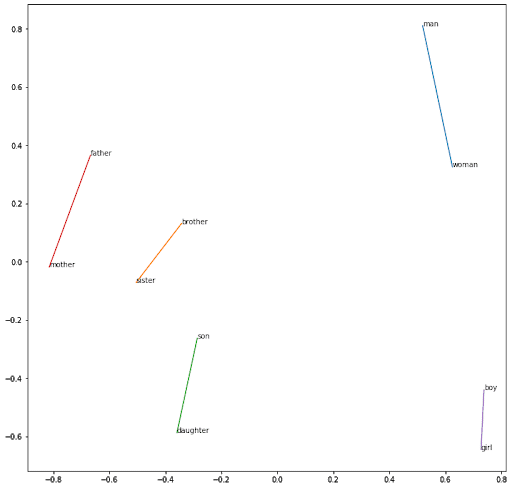
Men – 𝑀𝑎𝑛 + 𝑊𝑜𝑚𝑎𝑛 = Women
Unter Verwendung der oben definierten Operation und einer Metrik für die Kosähnlichkeit sind die fünf ähnlichsten Wörter :
women - 0.2889893054962158 weiblich - 0.272260844707489 strangers - 0.24558939039707184 teens - 0.2443128377199173 daughters - 0.24117740988731384
Das Ergebnis für Zombies – Zombie + 𝑊𝑜𝑚𝑎𝑛 :
women - 0.2547883093357086 weiblich - 0.23258551955223083 ladies - 0.22764989733695984 stripper - 0.22274985909461975 develops - 0.2202150821685791
Das Ergebnis für Men – Man + Soldier :
soldiers - 0.3547001779079437 daughters - 0.21896378695964813 letters - 0.21452251076698303 backyard - 0.21437858045101166 veterans - 0.21067838370800018
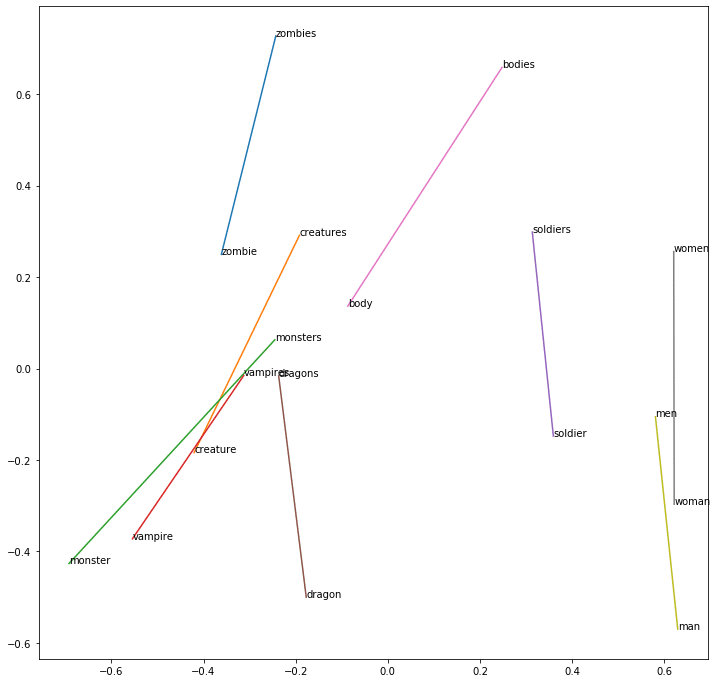
Das Ergebnis für Zombies – Zombie + Monster :
werewolves - 0.2724993824958801
monsters - 0.25695472955703735
creature - 0.24453674256801605
Drachen - 0.22363890707492828
bloke - 0.21858260035514832
Hier scheinen die Wörter „monsters“ und „werewolves“ im Zusammenhang mit unserem Datensatz sehr ähnlich zu sein.
Mithilfe einer PCA können wir die Dimension der Zahleneigenschaft :
Mit der gleichen Argumentation wird das Geschlecht erfasst:
Mit der gleichen Argumentation zwischen Verben im Infinitiv und Verben, die auf -ed enden:
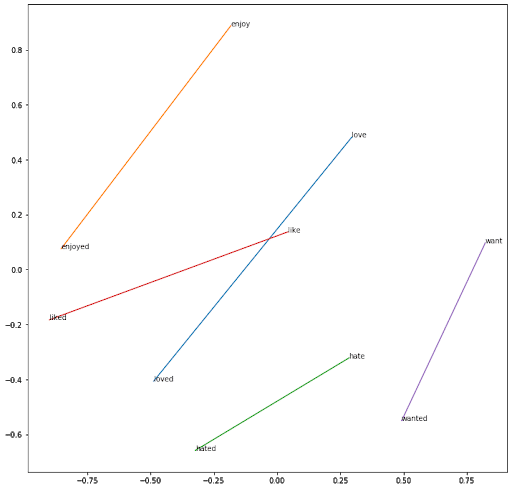
Das „word2vec embedding“ erfasst effektiv die semantischen und arithmetischen Eigenschaften eines Wortes. Es reduziert außerdem die Dimension des Problems und damit die Lernaufgabe.
Wir können uns vorstellen, den word2vec-Algorithmus zu verwenden, um die Einbettungsmatrix des Klassifikationsmodells vorab zu trainieren. Infolgedessen wird unser Klassifikationsmodell während der Lernphase der Gefühle eine viel bessere Darstellung der Wörter haben.
Hast du Lust, eine ausführlichere Schulung zu den verschiedenen Aspekten, die in diesem Artikel behandelt werden, zu beginnen?