Eine Zeitreihe ist eine Datentabelle, die die Entwicklung einer Variablen im Laufe der Zeit wiedergibt. In Python wird die Zeitreihe oft in Form einer Pandas-Reihe verarbeitet, die durch ein DateTime indiziert ist. Dieses Format ist sehr einfach zu verarbeiten und zu visualisieren.
Zeitreihen werden in vielen Bereichen wie z. B. der Astronomie und der Meteorologie verwendet, aber wahrscheinlich am häufigsten in der Wirtschaft. Man denke z. B. an die Aktienkurse von Unternehmen oder auch an die Entwicklung der Temperaturen im Laufe der Zeit.
Der ARMA-Prozess
AR
Eine erste Modellierung von Zeitreihen kann mithilfe des AR- oder Autoregressiven Modells erfolgen. Dieses Modell zielt darauf ab, den Wert unserer Zeitreihe zu einem Zeitpunkt t mithilfe einer Summe über die p vorherigen Zeitpunkte vorherzusagen.
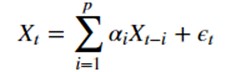
mit:
- Xt der Wert zu einem Zeitpunkt t
- epsilon t der Fehler zu einem Zeitpunkt t
- alpha i der Koeffizient, der mit Xt-i verbunden ist
MA
Der MA- oder Moving-Average-Prozess hingegen versucht, den Wert zu einem Zeitpunkt t aus den Fehlern der letzten q Zeitpunkte vorherzusagen.
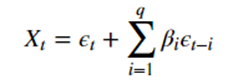
Dabei gilt Folgendes:
- Xt der Wert zu einem Zeitpunkt t
- epsilon t der Fehler zu einem Zeitpunkt t
- beta i der Koeffizient, der mit epsilon t-i verbunden ist
ARMA
Der ARMA-Prozess kombiniert einen AR- und einen MA-Prozess. Er wird als ARMA(p, q) bezeichnet. Die genaue mathematische Formel lautet wie folgt:
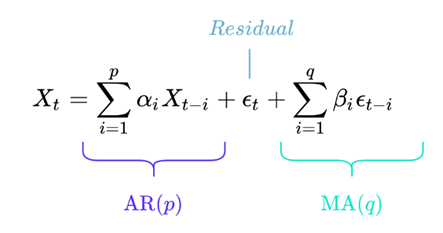
In der gleichen Schreibweise wie oben.
Auch wenn diese Formel erschreckend klingen mag, ist sie in Wirklichkeit sehr einfach zu verstehen.
Konkret bedeutet ein ARMA(1, 1)-Prozess Folgendes:
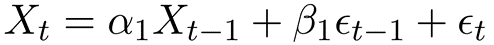
Grenzen des Modells
Dieses Modell ist zwar sehr einfach und liefert gute Ergebnisse, hat aber einige Einschränkungen. Zunächst einmal liefert dieses Modell nur gute Ergebnisse bei sogenannten stationären Zeitreihen, d. h. bei Zeitreihen, deren Mittelwert und Varianz konstant sind.
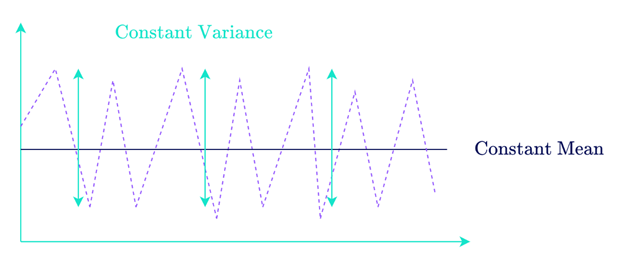
Außerdem ist es schwierig, die nächsten Werte für mehr als t + 1 vorherzusagen, da wir dann kein Feedback mehr über den Fehler unseres Modells für den MA-Teil haben.
Python-Studie
Erste Analyse
Um mit der Analyse der Zeitreihe zu beginnen, importieren wir die Pandas-Bibliothek und Matplotlib, die für die Visualisierung verwendet wird.
In dieser Befehlszeile sind neben dem Namen der Datei, die gelesen werden soll, die Argumente für die Funktion:
- parse_dates: Dieses Argument teilt pandas mit, dass der Dataframe eine Datumsspalte enthält und dass diese die erste Spalte ist.
- index_col: gibt an, dass der Index ebenfalls die erste Spalte ist.
- squeeze: ermöglicht die Rückgabe einer Series und nicht eines Dataframes.
Um unsere Analyse zu beginnen, können wir unsere Zeitreihe ganz einfach mithilfe der Bibliothek matplotlib.pyplot visualisieren, indem wir die folgende Funktion verwenden:
Mithilfe dieser Funktion erhältst du ein Diagramm, das die Entwicklung unserer Variable im Laufe der Zeit zeigt.

Stationaritätstest
Anschließend wird ein Stationaritätstest durchgeführt. Der Dickey-Fuller-Test liefert schnell gute Ergebnisse und ist in Python bereits in der Bibliothek Statsmodels implementiert.
Indem wir die Funktion importieren und sie wie folgt verwenden, können wir feststellen, ob unsere Zeitreihe durch einen ARMA-Prozess modelliert werden kann:
Dieser Code-Schnipsel ruft den p-Wert des Dickey-Fuller-Tests für die Reihe ab. Dieser Wert gibt an, ob die Reihe als stationär angesehen werden kann. Normalerweise wird sie als stationär angesehen, wenn der Wert unter 0,05 liegt. Hier liegt unser p-Wert bei 0,053. Wir befinden uns also an der Grenze zur Stationarität, da die Varianz der Reihe nicht wirklich konstant ist, aber du wirst sehen, dass dies später kein Problem darstellt.
Modellierung
Dazu wird ein ARMA-Modell erstellt, dessen Parameter so angepasst werden müssen, dass sie der Zeitreihe so gut wie möglich entsprechen, was sich als schwierig erweisen kann.
Hier entsprechen die Begriffe p und q der ersten bzw. letzten Stelle des Arguments order der Funktion. Die am Ende hinzugefügte Methode fit dient dazu, das Modell zu trainieren, damit es seine Parameter allein bestimmt.
Mit der Methode summary können wir überprüfen, ob unser Modell gut ist:
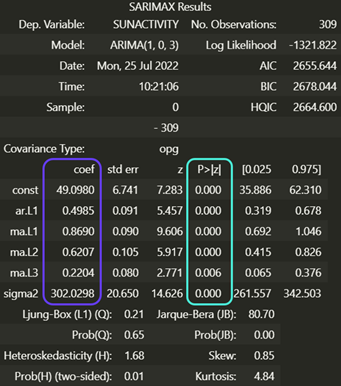
Diese Tabelle mag beeindruckend erscheinen, ist aber in Wirklichkeit sehr einfach zu interpretieren. Die lila umrandete Spalte entspricht den Parametern des Modells und die blau umrandete Spalte gibt den p-Wert jedes Parameters an. Hier sieht man, dass die Parameter gut sind, denn der p-Wert ist immer kleiner als 0,05. Wenn das nicht der Fall ist, kann man p und q ändern, um unnötige Parameter zu entfernen.
So kannst die Ergebnisse aufrufen und ansehen:
In Rot ist unser Modell dargestellt, in Blau die tatsächlichen Werte:
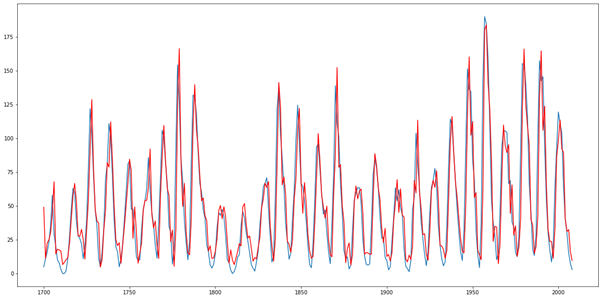
Fazit
Zusammenfassend lässt sich sagen, dass wir unsere Zeitreihe modellieren konnten, aber unser Modell hat einige Einschränkungen, die wir weiter oben besprochen haben. Um nicht-stationäre Zeitreihen zu behandeln, können wir das ARIMA-Modell verwenden, das eine Differenzierung hinzufügt. Wenn unsere Reihe Saisonalität aufweist, d. h. Schwankungen in einem regelmäßigen Zeitintervall, solltest du eher das SARIMA-Modell verwenden. Diese Modelle und noch mehr werden in unserer Weiterbildung für Data Scientists behandelt.