Um ein Vorhersagemodell zu definieren, verwenden Datenwissenschaftler eine Vielzahl von Beobachtungen. Doch während die Untersuchung dieser Beobachtungen zu einem optimalen Ergebnis führt, haben die Datenexperten oft nur wenig Zeit, um alle Hypothesen zu analysieren.
Wie kann man also in kürzester Zeit das richtige Modell finden? An dieser Stelle kommt die Bayes’sche oder Bayesianische Optimierung ins Spiel. Worum geht es dabei? Wie funktioniert sie? Die Antworten findest du hier.
Was ist der bayesianische Ansatz?
Die bayesianische Optimierung leitet sich direkt aus dem Bayes’schen Theorem ab:
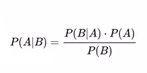
Durch dieses Theorem hast du einen Wert y, der eine Funktion von x ist. Die Idee ist nun, den Wert von x zu bestimmen, indem man den Wert von y optimiert. In diesem Fall besteht x aus einem Satz von Parametern (oder Beobachtungen).
Konkret kann dies in einer Vielzahl von Situationen angewendet werden, z. B. bei der Festlegung eines idealen Preises zur Maximierung der Gewinnspanne, bei der Konfiguration einer Anwendung oder einer Datenbank zur Maximierung ihrer Leistung, bei der Verwaltung von Parametern zur Optimierung des überwachten Lernens etc.
Bei all diesen Annahmen steht den Data Scientists nur eine begrenzte Anzahl von Beobachtungen zur Verfügung, um ein optimales Ergebnis zu erzielen (sei es aufgrund von zeitlichen, finanziellen oder materiellen Beschränkungen).
Denn um das beste Modell zu definieren, müssen in der Regel viele Hypothesen getestet, mehrere Trainings durchgeführt und Validierungen vorgenommen werden. All diese Testphasen sind jedoch zeitaufwendig. Daher ist es nicht möglich, eine unbegrenzte Anzahl von Hypothesen zu untersuchen.
Um diese Einschränkungen zu bewältigen, wurde die Bayes’sche Optimierung eingeführt.

Wie funktioniert die bayesianische Optimierung?
Die zentrale Idee der bayesianischen Optimierung ist es, die Anzahl der Beobachtungen zu minimieren und gleichzeitig schnell zur optimalen Lösung zu konvergieren. Um dies zu erreichen, muss man drei grundlegende Prinzipien kennen.
Der Gaußsche Prozess
Die Idee des bayesianischen Ansatzes ist es, bekannte Beobachtungen zu nutzen, um daraus Wahrscheinlichkeiten für Ereignisse abzuleiten, die noch nicht beobachtet wurden. Um zu dieser Schlussfolgerung zu gelangen, muss für jeden Wert X die Wahrscheinlichkeitsverteilung bestimmt werden.
Die effektivste Methode dafür ist zweifellos der Gaußsche Prozess. Dieser ermöglicht es, den wahrscheinlichsten Wert (genannt Mittelwert µ) und die wahrscheinliche Streuung des Wertes um den Mittelwert (genannt Standardabweichung σ) zu identifizieren. Diese Standardabweichung σ wird schwächer, je näher du dich einem bereits beobachteten Punkt näherst.
Idealerweise solltest du diese Werte und Abstände für jeden Beobachtungspunkt berechnen. In der Praxis ist diese umfassende Darstellung jedoch aus Zeitgründen nicht möglich. Daher sollten die zu bewertenden Punkte ausgewählt werden.
💡Auch interessant:
| Standardabweichung Excel |
| WENN Funktion Excel |
| Dropdown Liste Excel |
| Excel Spalte Zeile fixieren |
Exploration und Betrieb
Um ein leistungsfähiges Vorhersagemodell zu entwerfen, müssen Data Scientists die relevantesten Punkte definieren. Dies geschieht in zwei Schritten:
- Die Exploration: Diese ist dann interessant, wenn die Standardabweichung besonders groß ist. Mit anderen Worten: Die unbekannte Variable im Suchraum ist hoch. Dies ermöglicht es, mehrere Modelle zu testen und das Wissen über die zu optimierende Funktion zu verbessern.
- Auswertung: In diesem Stadium geht es darum, die zuvor getesteten Modelle zu verfeinern. Die Idee ist, den maximalen oder höchsten Punkt zu finden. Dazu werten die Data Scientists den Mittelwert µ aus. Wenn der Mittelwert µ in den Extremen liegt, ist es einfacher, das richtige Modell zu identifizieren.

Beachte, dass du das richtige Gleichgewicht zwischen Erkundung und Betrieb finden musst. Wenn du dich auf die Erkundung konzentrierst, kann es sein, dass du andere Modelle, die vielleicht besser sind, übersiehst. Wenn du dich hingegen auf die Ausbeutung konzentrierst, könntest du notwendige Verbesserungen übersehen.
Die Akquisitionsfunktion
Die Akquisitionsfunktion hilft dabei, den richtigen Kompromiss zwischen diesen beiden Variablen zu finden. Denn für jeden Punkt im Suchraum identifiziert die Funktion ein Optimierungspotenzial. Unter all diesen Punkten identifiziert die Funktion ein Maximum. Das ist der nächste Punkt, der getestet wird. Die Berechnung wird so oft wiederholt, bis eine Konvergenz zwischen dem Maximum und dem Minimum erreicht ist. Mit diesem Parameterpaar sollte die beste Leistung erzielt werden.
Gut zu wissen: Rauschen kann die Daten verfälschen und das Lernen erschweren. Um dies zu vermeiden, ist es wichtig, dass die Umgebung stabil und die Beobachtungen reproduzierbar sind, bevor du die Bayes’sche Optimierung anwendest.
💡Auch interessant:
Wie lässt sich die bayesianische Optimierung in die Praxis umsetzen?
Um die Berechnungen der bayesianischen Optimierung zu vereinfachen, ist es am einfachsten, gute Werkzeuge zu verwenden. Wie das Python-Paket scikit-optimize oder bayesian-optimization. Du musst dann nur einen Suchraum definieren, und das Tool wird sich dann darum kümmern, die Punkte mit hohem Potenzial zu finden, insbesondere mithilfe des Gaußschen Prozesses. Auch hier musst du Python neu starten, bis du ein zufriedenstellendes Ergebnis erhältst.