La qualité des performances de l’apprentissage automatique dépend en grande partie des informations disponibles. C’est pourquoi, les Data Scientists doivent étudier avec attention les jeux de données utilisés. Pour cela, ils disposent d’un large panel d’outils statistiques. Parmi lesquels, le kurtosis. Alors de quoi s’agit-il ? À quoi ça sert ? Découvrez les réponses.
Qu’est-ce que le Kurtosis ?
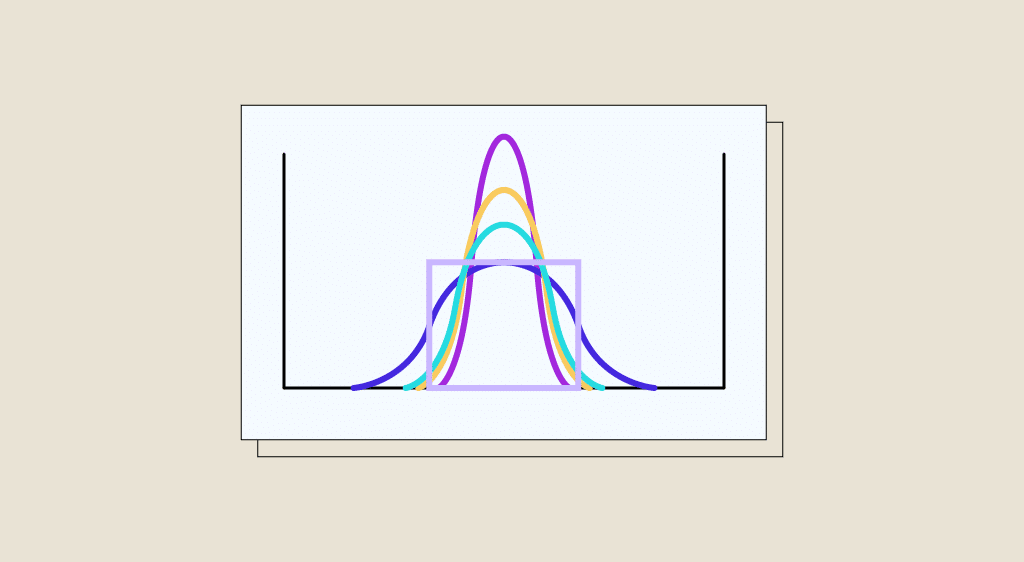
Venant du nom grec ancien κύρτωσις (signifiant courbure), le Kurtosis est un outil statistique permettant de mesurer l’acuité et l’aplatissement de la distribution d’une valeur aléatoire réelle.
L’aplatissement correspond à la probabilité et/ou fréquence d’apparition des valeurs aberrantes (soit des valeurs extrêmement élevées ou extrêmement basses par rapport à la moyenne). Sur une courbe, cela représente les extrémités situées de chaque côté d’une distribution.
Bon à savoir : on parle aussi de coefficient d’acuité, coefficient d’aplatissement et degré de voussure.
Quels sont les différents types de Kurtosis ?
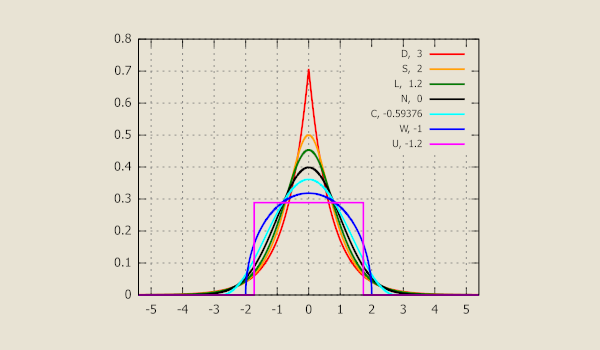
Selon leur niveau d’aplatissement, les distributions peuvent être classées en 3 catégories.
Les distributions mésokurtiques
Ce sont les distributions à aplatissement moyen. Autrement dit, les valeurs aberrantes ne sont ni très fréquentes, ni très rares.
Le Kurtosis est toujours mesuré par rapport à un Kurtosis normal. Par principe, la distribution normale a un Kurtosis de 3. Si tel est le cas, toutes les distributions présentant un Kurtosis similaire seront considérées comme mésokurtiques.
Bon à savoir : bien souvent, le Kurtosis est décrit à travers un excès de Kurtosis, Soit -3. Cet aplatissement excédentaire facilite la comparaison des distributions par rapport à la norme. Mais ici, l’excès de Kurtosis normal a une valeur égale à 0. Et là encore, toutes les distributions présentant un Kurtosis proche de 0 seront considérées comme mésokurtiques.
Ce type de distribution concerne par exemple le poids de naissance des bébés. Même s’il y a des valeurs aberrantes (5 ou 2 kilogrammes à la naissance), elles ne sont ni très fréquentes, ni très peu fréquentes.
Les distributions platykurtiques
Il s’agit des distributions à faible aplatissement (ce sont les queues fines). Ce qui signifie que les valeurs aberrantes sont très peu fréquentes.
Dans ce cas, le Kurtosis est moins élevé qu’une distribution normale. Il est inférieur à 3, et l’excès de Kurtosis inférieur à 0. C’est pourquoi, on parle également d’aplatissement négatif, car l’excès d’aplatissement est négatif.
Bon à savoir : le nom de PlatyKurtosis (et plus exactement le terme platy) vient du grec platús, qui signifie plat. Cela s’explique, car de nombreuses distributions platykurtiques ont un pic aplati, même si certaines peuvent être pointues. Mais attention, le Kurtosis mesure la longueur de l’aplatissement (les deux extrémités de la distribution), et non le « pic ». PlatyKurtosis vient donc d’une confusion des statisticiens de l’époque, mais le terme est resté.
Sur une courbe, une distribution platykurtique se traduit généralement par une distribution uniforme. Il n’y a presque pas de variations entre les différentes variables.
Ça serait par exemple le cas d’une étude sur l’utilisation des réseaux sociaux par des lycéens. Ici, ils ont presque tous le même âge, et utilisent également presque tous les médias sociaux, quel que soit leur âge. Il n’y a pas ou peu de valeurs aberrantes (au sein d’un lycée, peu d’élèves auraient plus de 18 ans ou moins de 14 ans).

Les distributions leptokurtiques
Ce sont les distributions à aplatissement élevé (on parle aussi de queue large). Autrement dit, il y a beaucoup de valeurs aberrantes. Ces dernières sont donc plus élevées qu’une distribution normale. Cela se traduit par un Kurtosis supérieur à 3 et un excès de Kurtosis supérieur à 0. Ici, on parle de Kurtosis positif.
Une distribution leptokurtique pourrait par exemple concerner la distance de la terre avec d’autres étoiles de l’univers. Certaines sont relativement proches (ou du moins accessibles) alors que d’autres sont à des centaines d’années lumières.

À quoi sert le Kurtosis ?
En déterminant la disparité des valeurs au sein d’une distribution, le Kurtosis figure parmi les outils statistiques incontournables. Il peut ainsi s’appliquer à une grande variété de secteurs d’activité.
Voici les plus courants :
- L’analyse financière : le Kurtosis permet de mesurer le risque de volatilité du prix d’un investissement. Si le Kurtosis est élevé (dans le cas d’une distribution leptokurtique), cela signifie que l’investissement choisi produira occasionnellement des rendements extrêmes. Ce qui peut permettre de multiplier les gains de façon exponentielle, mais aussi de perdre beaucoup d’argent. À l’inverse, un portefeuille d’actions avec une faible valeur de Kurtosis indique un rendement plus stable et prévisible. Donc moins de risque, mais aussi moins de profit.
- Le Machine Learning : il s’agit ici de mesurer la disparité d’un dataset. Pour autant, cela ne signifie pas que les données disponibles sont mauvaises. L’idée est surtout de permettre aux Data Scientists de mieux comprendre le jeu de données afin d’améliorer les performances en apprentissage automatique.
Quelles différences entre Skewness et Kurtosis ?
Pour mesurer la disparité d’un jeu de données, les Data Scientists peuvent utiliser le Kurtosis ou le skewness. Dans le second cas, il s’agit surtout de mesurer la répartition de la distribution autour de la valeur centrale. À l’inverse, le Kurtosis mesure davantage la fréquence des valeurs aberrantes.
Mais dans les deux cas, il s’agit d’outils de mesure incontournables pour l’apprentissage automatique.
Vous souhaitez en savoir plus sur le Machine Learning ?
Au-delà des outils statistiques, le Machine Learning nécessite des compétences variées en matière d’analyse prédictive, de langage informatique, de bases de données, … À ce titre, il est plus que nécessaire de se former en science de la donnée. C’est justement pour cette raison que nous vous proposons la formation Data Scientist. Découvrez-la !