Connaissez vous l'ACP ? Méthode très utile et utilisée en réductions de dimensions, découvrez son fonctionnement dans cet article.
Qui n’a jamais eu entre les mains un jeu de données contenant un très grand nombre de variables sans savoir lesquelles sont les plus importantes ? Comment réduire ce jeu de données afin de le représenter de manière simple sur 2 ou 3 axes ? Voici l’ACP !
L’analyse en composantes principales vient répondre à ces questions. En fait, l’ACP est une méthode bien connue de réduction de dimension qui va permettre de transformer des variables très corrélées en nouvelles variables décorrélées les unes des autres.
Le principe est simple : Il s’agit en fait de résumer l’information qui est contenue dans une large base de données en un certain nombre de variables synthétiques appelées : Composantes principales.
L’idée est ensuite de pouvoir projeter ces données sur l’hyperplan le plus proche afin d’avoir une représentation simple de nos données.
Évidemment, qui dit réduction de dimension dit perte d’informations. C’est là tout l’enjeu que représente une Analyse en Composantes principales. Il faut pouvoir réduire la dimension de nos données tout en conservant un maximum d’informations.
Comment fonctionne une Analyse en Composantes Principales ?
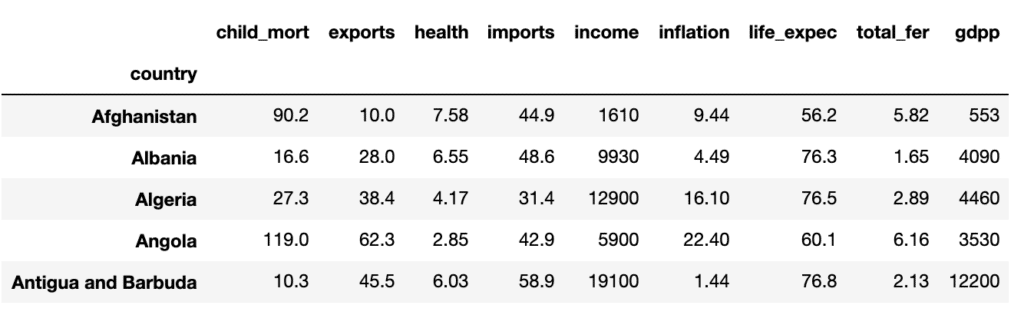
Pour illustrer le principe de l’ACP, nous allons prendre pour exemple un jeu de données nommé ‘country_data’ qui comme son nom l’indique regroupe plusieurs informations (PIB ; Revenu moyen ; Espérance de vie ; Taux de natalité/mortalité etc…) sur différents pays.
En voici les 5 premières lignes :
Par la suite il est important de centrer et réduire nos variables pour atténuer l’effet d’échelle car elles ne sont pas calculées sur la même base.
Une fois cette étape réalisée, il faut voir nos données comme une matrice à partir
de laquelle nous allons calculer des valeurs propres et vecteurs propres.
En algèbre linéaire, la notion de vecteur propre correspond à l’étude des axes privilégiés, selon lesquels une application d’un espace dans lui-même se comporte comme une dilatation, multipliant les vecteurs par une constante appelée valeur propre. Les vecteurs auxquels il s’applique s’appellent vecteurs propres, réunis en un espace propre
Après avoir importé le module PCA de sklearn.decomposition, les valeurs propres renvoyés sont les suivants
Les valeurs propres sont :[3.48753851 1.47902877 1.15061758 0.93557048 0.65529084 0.15140052]
Ces valeurs propres vont nous permettre de déterminer le nombre de facteur/Composantes principales optimal pour notre ACP. Par exemple, si le nombre optimal de composantes est 2, alors nos données seront représentées sur deux axes et ainsi de suite.
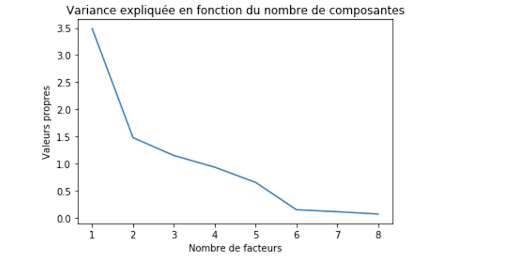
Sur ce graphe qui représente le nombre de facteurs à choisir en fonction des valeurs propres nous indiquent que le choix optimal de facteur est de 2 (grâce à la méthode du coude). Ainsi, nous allons passer d’une dimension 9 à une dimension 2 ce qui réduit considérablement la dimension de base. Comme dit précédemment, il y aura forcément une perte d’information à la suite de cette réduction. Cependant, on garde tout de même un taux d’informations de quasiment 70% ce qui nous permettra d’avoir une représentation proche de ma représentation en 9 dimensions.
Le module ACP ayant calculé les coordonnées de nos données, il ne reste plus qu’à les représenter mais avant ça, nous allons nous intéresser à un outil très souvent utilisé lorsque l’on fait une Analyse en Composantes Principales, c’est le cercle des corrélations.
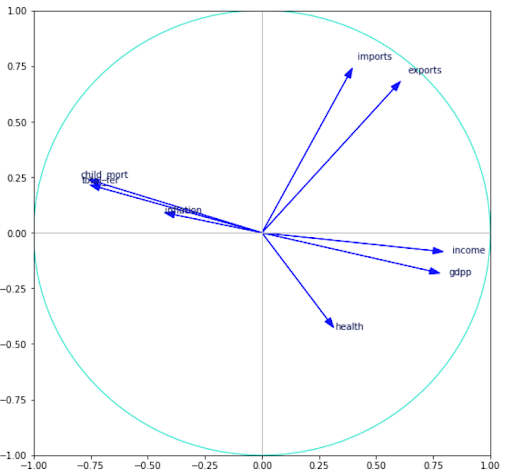
Notre représentation se faisant sur 2 axes, le cercle des corrélations est un outil pratique nous permettant de visualiser l’importance de chaque variable explicative pour chaque axe de représentation. La direction de chaque flèche indique l’axe expliqué par la variable et le sens indique si la corrélation est positive ou négative. On remarque que des variables comme ‘income’,’gdpp’ et ‘health’ sont corrélées positivement au premier axe alors que ‘child_mort’ ou ‘total_fer’ le sont aussi mais négativement. On peut alors s’intéresser à la représentation des pays dans les deux axes choisis par l’ACP et voir l’influence de la variable ‘life_expec’ sur leurs représentations.
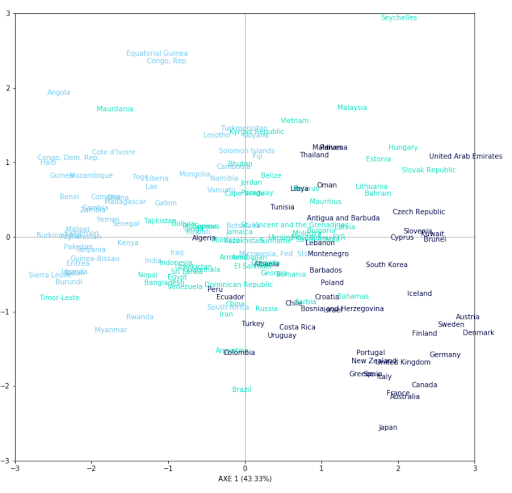
Voici une représentation de chaque pays (167) sur 2 axes. Pour juger de la qualité de notre représentation, nous avons décidé de colorer chaque pays en fonction de l’espérance de vie de chacun selon 3 groupes, nous pouvons observer une certaine tendance. On peut alors remarquer que les pays avec une espérance de vie élevée sont concentrés dans la partie inférieure droite du graphe. D’après le cercle des corrélations les individus se trouvant dans cette partie sont en partie expliqués par les variables ‘health’, ‘income’ ou ‘gdpp’. On peut alors en conclure que les pays dépensant le plus dans la santé ont une espérance de vie plus élevée. De même pour les pays se trouvant dans la partie supérieure gauche du graphe. D’après le cercle des corrélations, cette partie est majoritairement expliquée par les variables ‘child_mort’ ou ‘total_fer’.
Si vous souhaitez en savoir plus sur l’Analyse en Composantes Principales ou sur d’autres méthodes de réduction de dimensions, plusieurs modules y sont consacrés dans notre formation Data Analyst.