Le clustering est une discipline particulière du Machine Learning ayant pour objectif de séparer vos données en groupes homogènes ayant des caractéristiques communes. C’est un domaine très apprécié en marketing, par exemple, où l’on cherche souvent à segmenter les bases clients pour détecter des comportements particuliers.
Dans un précédent article, nous avions présenté un premier algorithme de clustering : celui des K-moyennes ou K-means.
Dans cet article nous allons détailler le fonctionnement de l’algorithme CAH. La Classification Ascendante Hiérarchique : CAH est un algorithme non supervisé très connu en matière de Clustering.
Les champs d’application sont divers : segmentation client, analyse de donnée, segmenter une image, apprentissage semi-supervisé….
Le Principe
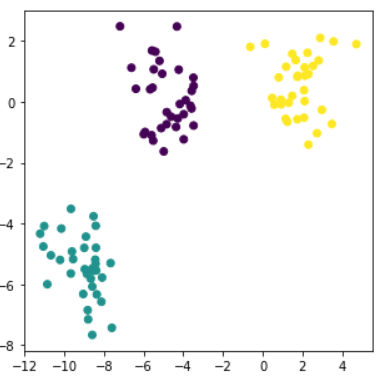
Étant donnés des points et un entier k, l’algorithme vise à diviser les points en k groupes, appelés clusters, homogènes et compacts. Regardons l’exemple ci-dessous :

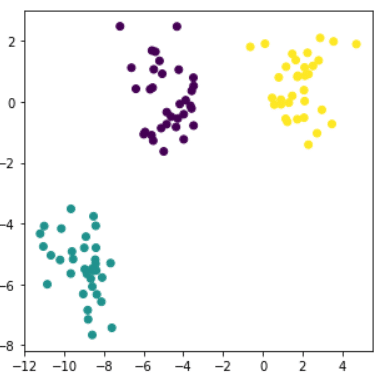
Sur ce jeu de données en 2D il apparaît clair que l’on peut le diviser en 3 groupes. Concrètement comment s’y prend-on ?
- L’idée de départ est de considérer que chacun des points de votre jeu de données est un centroïde. Cela revient à considérer qu’à chaque point correspond une unique étiquette (0,1,2,3, 4…).
- Ensuite on regroupe chaque centroïde avec son centroïde voisin le plus proche. Ce dernier prend l’étiquette du centroïde qui l’a « absorbé ».
- On calcule alors les nouveaux centroïdes qui seront les centres de gravité des clusters nouvellement créés.
- On réitère l’opération jusqu’à obtenir un unique cluster ou bien un nombre de clusters préalablement défini.
Dans notre exemple le nombre de clusters optimal est 3 et le résultat final se trouve sur la figure de droite.
Pour mieux comprendre le mécanisme on peut le représenter avec un schéma simple :

Au début, chaque lettre est considérée comme un cluster puis on les regroupe au fur et à mesure selon leur proximité pour ne former à la fin qu’un seul groupe : abcdef.
Notion de distance et critère
Vous l’aurez compris dans cet algorithme trois points sont clé :
Quelle est la métrique utilisée pour évaluer la distance entre les centroïdes ? Quel est le nombre de clusters à choisir ? Sur quel critère décide-t-on de regrouper les centroïdes entre eux ?
Dans la classification ascendante hiérarchique généralement on utilise la distance euclidienne, soient p = (p1,….,pn) et q = (q1,….,qn)
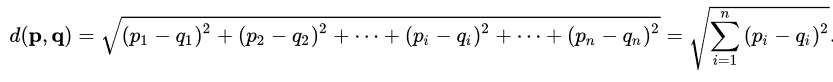
Elle permet d’évaluer la distance entre les centroïdes. A chaque étape de regroupement entre deux centroïdes on obtiendra un nouveau cluster et un nouveau centroïde qui n’est autre que le centre de gravité du nuage de points comme expliqué plus haut.
C’est là qu’intervient la notion d’inertie intraclasse. Il s’agit simplement de la somme des distances euclidiennes entre chaque point associé au cluster et le centre gravité nouvellement calculé. Bien évidemment quand vous allez regrouper des clusters entre eux vous allez augmenter l’inertie intraclasse. Tout le challenge est de faire en sorte de minimiser cette augmentation. Ainsi si vous avez le choix de regrouper un cluster avec 4 ou 5 autres clusters différents vous choisirez celui qui minimise le gain d’inertie intraclasse. Cette méthode est le principe du critère de Ward qui est très souvent utilisé pour la Classification Ascendante Hiérarchique. Il existe d’autres critères mais le critère de Ward est celui utilisé par défaut quand on implémente une CAH en python avec Scikit Learn.
Dans l’exemple précédent il était aisé de trouver le nombre idéal de clusters simplement en visualisant graphiquement. Généralement les jeux de données ont plus de deux dimensions et il est donc difficile de visualiser le nuage de points et d’identifier rapidement le nombre de clusters optimal. On peut décider la CAH en lui donnant un nombre de clusters au préalable. Supposons dans l’exemple précédent que nous n’avions pas visualisé les données avant et nous décidons de tester différentes fois avec un nombre de clusters différents. Voici les résultats obtenus :
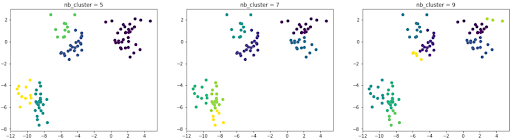
Le partitionnement est inexact car le nombre de clusters optimal est 3. Une méthode connue pour trouver le nombre de cluster optimal est d’utiliser un dendrogramme comme celui-ci :
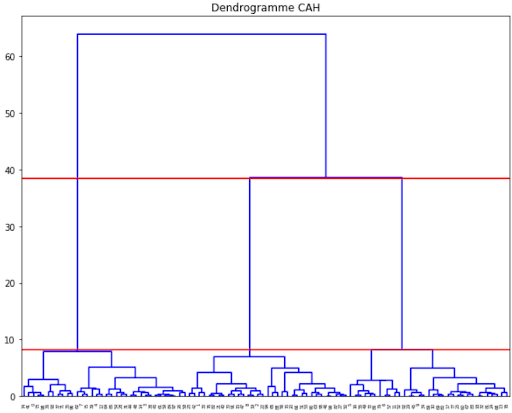
Il permet de visualiser les regroupements successifs jusqu’à obtenir un unique cluster. Il est souvent pertinent de choisir le partitionnement correspondant au plus grand saut entre deux clusters consécutifs.
Le nombre de clusters correspond alors au nombre de lignes verticales traversée par la coupe horizontale du dendrogramme. Dans notre exemple ci-dessus la coupe horizontale correspond aux deux lignes rouges. Il y a 3 lignes verticales traversées par la coupe. On en déduit que le nombre de clusters optimal est 3.
Passons à la pratique en Python
L’entraînement d’une Classification Ascendante Hiérarchique est facilité avec la librairie Scikit-Learn. Un jeu de données comme celui qui a servi d’exemple se crée facilement avec la fonctionalité make_blobs de Scikit-Learn.
Une fois notre jeu de données générés, nous pouvons passer à l’implémentation d’une CAH. Nous allons utiliser la librairie Scikit-Learn.
Voici comment l’implémenter en code :
L’attribut n_clusters permet de renseigner le nombre de clusters souhaité pour la classification. Par défaut la distance utilisée est la distance euclidienne. Également le « critère de regroupement » appelé linkage est par défaut le critère de Ward.
Les limites de la Classification Ascendante Hiérarchique
Comme nous l’avons vu l’algorithme demande en amont de définir le nombre de partitions. Cela demande d’en avoir une idée précise et même si nous avons vu une méthode pour optimiser sur certains jeux de données elle n’est pas infaillible. En effet les jeux de données avec des formes elliptiques par exemple poseront problème. Dans l’exemple ci-dessous on voit clairement deux groupes s’apparentent à deux ellipses. La figure de droite montre le résultat après utilisation d’une CAH. Il est clair que celle-ci n’a pas réussi à identifier nos deux ellipses.
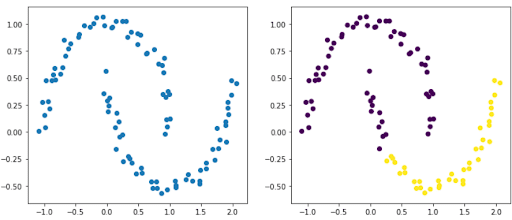
Également la classification ascendante hiérarchique peut s’avérer rapidement très coûteuse en temps et en ressource. Un moyen de contourner ce problème est de renseigner une matrice de connectivité. Il s’agit d’une matrice creuse indiquant quelles paires d’observation sont voisines.
L’utilisation d’un algorithme de clustering tel que la Classification Ascendante Hiérarchique n’est pas aisée suivant les données dont vous disposez. Il faudra souvent les retravailler. Chez Datascientest nous vous apprendrons à maîtriser les principaux algorithmes de clustering ainsi qu’à les interpréter sur des jeux de données.
N’hésitez pas à venir découvrir nos offres de formation pour apprendre à maîtriser les algorithme de clustering mais également de nombreux d’autres domaines du Machine Learning.