La théorie des graphes est une branche des mathématiques et de l’informatique qui consiste à modéliser différents problèmes de la vie réelle sous forme de graphes. L’une des utilisations les plus classiques est la modélisation d’un réseau routier entre différentes villes. L’une des problématiques principales étant l’optimisation des distances entre deux points. Pour trouver le plus court chemin , on utilise souvent l’algorithme de Dijkstra. Revenons sur son fonctionnement dans cet article Voyons un exemple (tiré de Wikipedia) :
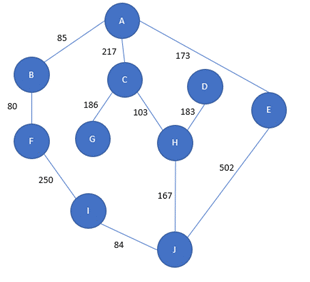
Ici les villes A à J sont représentées par les sommets du graphe.
Elles sont reliées par des routes qui correspondent aux arêtes du graphe. À chaque arête est associée une valeur que l’on appelle le poids. Elle correspond généralement à un coût ou à une distance.
Ici, chaque poids peut être vu comme la distance entre les deux villes reliées.
Très vite se pose un problème : comment déterminer le plus court chemin entre deux sommets ?
C’est là que l’algorithme de Dijkstra intervient !
Comment l’algorithme Dijkstra fonctionne ?
Imaginons que l’on cherche à trouver le plus court chemin entre la ville A et la ville J.
Tout au long de l’algorithme on va garder en mémoire le chemin le plus court depuis A pour chacune des autres villes dans un tableau.
On répète toujours le même processus :
- On choisit le sommet accessible de distance minimale comme sommet à explorer.
- A partir de ce sommet, on explore ses voisins et on met à jour les distances pour chacun. On ne met à jour la distance que si elle est inférieure à celle que l’on avait auparavant
- On répète jusqu’à ce qu’on arrive au point d’arrivée ou jusqu’à ce que tous les sommets aient été explorés.
C’est un peu vague tout ça …
Et concrètement ça donne quoi ?
Conclusion
Le tableau final nous donne la valeur du plus court chemin pour chacun des sommets du graphe. Par ailleurs, il garde en mémoire l’origine du point précédent permettant d’obtenir ce plus court chemin.
Par exemple, pour le sommet G, la valeur 403C nous indique qu’il faut 403 km pour l’atteindre et que ce plus court chemin passe juste avant par le point C. Il suffit donc de remonter le tableau pour obtenir le plus court chemin pour n’importe quel sommet.
Cette particularité explique l’intérêt de l’algorithme de Dijkstra : une seule itération permet d’obtenir le plus court chemin pour chaque sommet !
Pour aller plus loin :
- Il existe de nombreux autres algorithmes résolvant le problème du plus court chemin. Il faut cependant prendre garde aux conditions d’application de ces différents algorithmes. L’algorithme de tri topologique par exemple est plus efficace que l’algorithme de Dijkstra mais ne s’applique qu’à des graphes acycliques (sans aucune boucle).
- La complexité de l’algorithme de Dijkstra est polynomiale. Soit n le nombre de sommets et a le nombre d’arcs, elle est dans le pire des cas en O(a+ nlog(n))
- Edsger Dijkstra a découvert cet algorithme en 20 minutes alors qu’il cherchait la meilleure façon d’aller de Rotterdam à Groningen à la terrasse d’un café. Comme quoi un café peut résoudre beaucoup de problèmes.
Cet article vous a plu ? Notre formation Data Scientist comporte un cours sur la théorie des graphes. N’attendez plus, découvrez le cursus !










