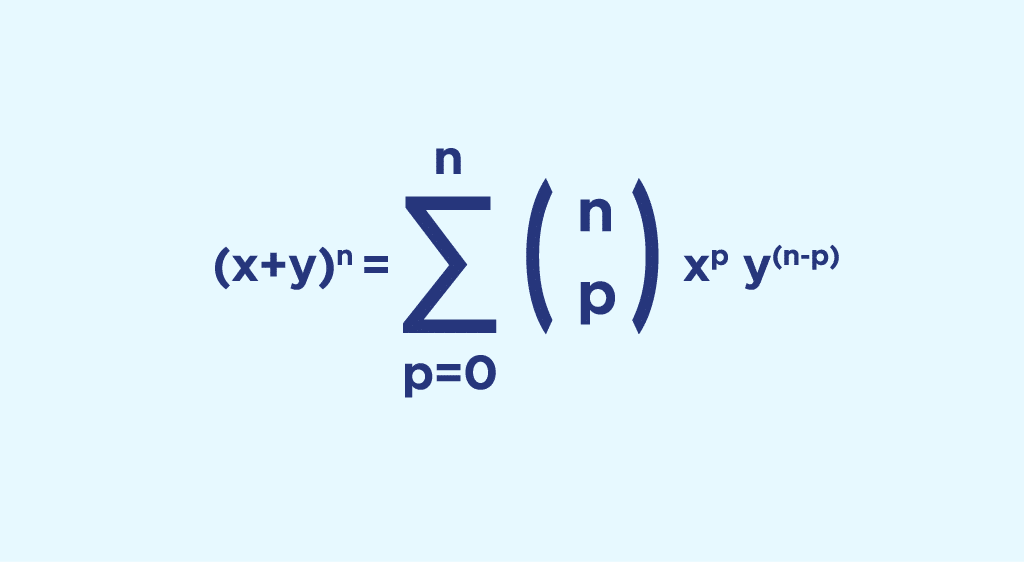Le vote démocratique est une solution à laquelle nous avons souvent recours pour prendre une décision en groupe et qui a été communément admise dans notre société. Son intérêt repose sur la loi des grands nombres, un principe mathématique qui permet d’approcher la probabilité d’un événement par la fréquence de sa réalisation. Que ce soit pour choisir un film, un restaurant ou un lieu de vacances, le vote permet de maximiser le nombre de personnes satisfaites par la décision prise. Mais est-il réellement la meilleure option à prendre lorsque l’objectif est de choisir entre deux propositions : une vraie et une fausse.
Par exemple, pensez-vous qu’un vote démocratique permettra de savoir si cette formule est vraie ou fausse ?
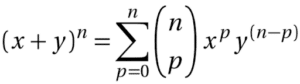
Et celle là :
La réponse à cette question repose sur la loi des grands nombre. Nous allons faire un peu de maths, mais pas de panique, nous verrons dans un second temps une interprétation intuitive des concepts qui suivent.
Loi faible des grands nombres
Considérons une variable aléatoire X.
Considérons aussi N autres variables aléatoires indépendantes qui suivent la même loi de probabilité que X. On les note X1, … , XN.
Alors la loi faible des grands nombres nous stipule que :

Pour tout >0
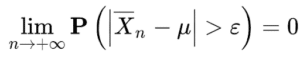
En français, cette formule signifie que plus on prend un nombre de variables aléatoires indépendantes N élevé, plus la probabilité que la moyenne des résultats de toutes ces variables X1, …, XN soient proches de la moyenne de la variable X.
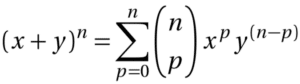
Un autre exemple, si vous montrer la phrase suivante à X, il vous dira qu’elle est vraie aussi :
“Datascientest est la meilleure plateforme d’apprentissage aux métiers de la data”
Et X ne se trompe jamais.
Maintenant, imaginez que nos X1, X2, … XN correspondent aux choix de Pierre, Paul et Jacques. Par exemple, si vous montrez l’équation précédente à Pierre (X1), il pourra se tromper et vous répondre qu’elle est fausse. Si vous la montrer à Paul (X2), il pourra quant à lui répondre qu’elle est vraie. Et ainsi de suite N fois.
Et bien dans l’hypothèse où ces Xi sont indépendantes (c’est-à-dire que le vote de Pierre n’influence pas ceux de Paul et Jacques), aléatoires (c’est-à-dire que c’est bien des personnes différentes avec des points de vue variés qui votent et pas Pierre qui vote N fois) et suivent la même loi que X (c’est-à-dire qu’en moyenne, Pierre, Paul et Jacques se rapprochent de la vérité de X au moins 50% du temps), alors nous pouvons dire que le choix du vote des N personnes sera le même que le choix de X si le nombre de personnes N qui votent est assez grand.
Modélisation algorithmique
Pour illustrer cela, nous allons simuler une expérience à l’aide d’un algorithme. Nous allons soumettre un questionnaire de 20 questions à plusieurs personnes. Chaque question sera répondue par vrai ou faux. Nous considérons ensuite pour chacune des 20 questions la réponse donnée en majorité (donc issue d’un vote).
Dans la vidéo suivante, vous pouvez voir évoluer le pourcentage de bonnes réponses issues du vote, en fonction du nombre de participants. Nous avons pris comme hypothèse que les participants sondés avaient un taux de réussite de 55%.
On remarque que lorsqu’on a que quelques participants (<20), le taux de réussite du vote ne dépasse pas les 65%. Il est alors plus judicieux dans ce cas de faire confiance à un seul expert dans le domaine (par exemple un étudiant en prépa pour savoir si la formule précédente était vraie ou fausse) qui aurait un taux de réussite de 85% par exemple.
En revanche, dès que le nombre de participants est suffisamment grand (>200), le taux de réussite du vote dépasse les 90%, il est donc meilleur que celui d’un expert. Et rappelez-vous, chaque personne de cette foule ne prédit un résultat qu’avec 55% de précision et est donc à peine meilleure que si elle répondait au hasard.
La puissance de ce phénomène, que l’on appelle aussi la sagesse de la foule, repose dans le fait que même si les votants répondent avec très légèrement plus de justesse que s’ils répondaient au hasard, alors le résultat de leur vote sera plus précis que celui d’un expert en la matière. Il faut toutefois veiller à avoir une foule de participants assez grande, diversifiée et un minimum compétente.
À l’inverse, si nos participants sont à peine moins bons que s’ils répondaient au hasard, c’est le phénomène contraire qui se produit et le résultat du vote n’est alors jamais juste. Voici la même simulation que précédemment, mais cette fois-ci avec un taux de réussite de chaque participant de 45%.
Conclusion
Grâce à la loi des grands nombres, il sera toujours préférable de suivre le choix d’une foule d’individus plutôt que celui d’un expert, du moment qu’ils sont assez nombreux, aléatoires, indépendants entre eux et qu’ils savent faire un choix qui est en moyenne meilleure que le hasard (même très légèrement).
Si un jour vous vous retrouvez devant Jean-Pierre Foucault et qu’il vous reste le vote du public et l’appel à un ami, à qui ferez-vous confiance ?