Clustering ist eine besondere Disziplin des Machine Learning, mit dem Ziel deine Daten in homogene Gruppen mit gemeinsamen Merkmalen aufzuteilen. Ein im Marketing sehr geschätztes Anwendungsgebiet, zum Beispiel dort, wo oft Kundenstämme zu segmentieren, um bestimmte Verhaltensweisen zu erkennen.
In den vorherigen Artikeln haben wir dir zwei Clustering Algorithmen erklärt: clustering : K-means und CAH Algorithmus- hieraschische aufsteigende Klassifizierung.
Deshalb erscheint es uns als wichtig, diesen Lernprozess mit dem DBSCAN fortzusetzen.
DBSCAN Algorithmus
DBSCAN ist ein sehr bekannter unüberwachter Algorithmus für Clustering. Er wurde 1996 von Martin Ester, Hans-Peter Kriegel, Jörg Sander und Xiawei Xu vorgeschlagen.
In diesem Artikel erklären wir dir, wie er funktioniert und wie es in Python mit Hilfe von Bibliotheken wie Scikit-Learn implementiert werden kann. Die Anwendungsbereiche sind vielfältig: Kartenanalyse, Datenanalyse, Segmentierung eines Bildes….
Das Prinzip
Wenn Punkte und eine ganze Zahl k gegeben sind, zielt der Algorithmus darauf ab, die Punkte in k homogene und kompakte Gruppen, sogenannte Cluster, zu unterteilen. Schauen wir uns das folgende Beispiel an:
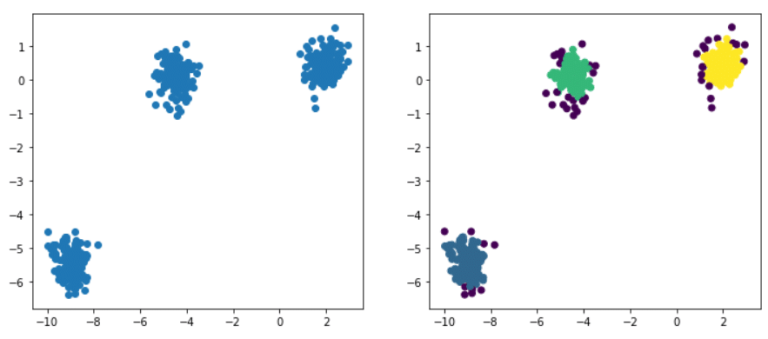
DBSCAN ist ein einfacher Algorithmus, der Cluster definiert, indem er die Schätzung der lokalen Dichte verwendet. Er kann in vier Schritte unterteilt werden:
- Für jede Beobachtung schaust du dir die Anzahl der Punkte an, die höchstens einen ε-Abstand von ihr entfernt sind. Diesen Bereich nennt man die ε-Nachbarschaft der Beobachtung.
- Wenn eine Beobachtung mindestens eine bestimmte Anzahl von Nachbarn hat, einschließlich sich selbst, wird sie als Kernbeobachtung betrachtet. In diesem Fall wurde eine Beobachtung mit hoher Dichte entdeckt.
- Alle Beobachtungen in der Nähe einer Core-Beobachtung gehören zu demselben Cluster. Es können auch Herzbeobachtungen in unmittelbarer Nähe zueinander sein. Das bedeutet, dass es eine lange Folge von Herzbeobachtungen gibt, die einen einzigen Cluster bilden.
- Jede Beobachtung, die keine Kernbeobachtung ist und keine Kernbeobachtung in ihrer Nachbarschaft hat, wird als Anomalie betrachtet.
Du musst also zwei Informationen festlegen, bevor du den DBSCAN benutzen kannst:
Wie groß ist die Entfernung ε, um für jede Beobachtung die ε-Nachbarschaft zu bestimmen? Welche minimale Anzahl von Nachbarn ist notwendig, um eine Beobachtung als Kernbeobachtung zu betrachten?
Diese beiden Informationen werden vom Nutzer frei eingegeben. Im Gegensatz zum k-Mittelwert-Algorithmus oder der hierarchischen aufsteigenden Klassifizierung muss die Anzahl der Cluster nicht vorab festgelegt werden, was den Algorithmus weniger starr macht.
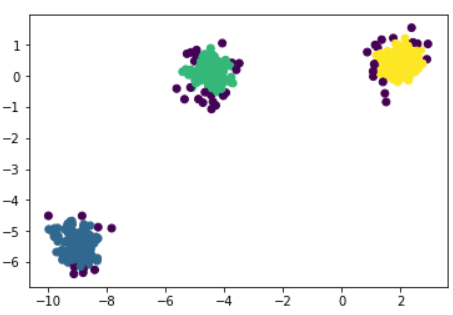
Ein weiterer Vorteil von DBSCAN ist, dass es auch mit Ausreißern oder Anomalien umgehen kann. In der obigen Abbildung siehst du, dass der Algorithmus drei Hauptcluster ermittelt hat: blau, grün und gelb. Die violett gefärbten Punkte sind Anomalien, die vom DBSCAN erkannt wurden. Natürlich kann die Partitionierung je nach dem Wert von ε und der Anzahl der minimalen Nachbarn variieren.
Begriff der Entfernung und Wahl des ε
In diesem Algorithmus sind zwei Punkte entscheidend:
Welche Metrik wird verwendet, um die Entfernung zwischen einer Beobachtung und ihren Nachbarn zu bewerten? was ist das ideale ε?
In DBSCAN wird normalerweise die euklidische Distanz verwendet, d.h. p = (p1,….,pn) und q = (q1,….,qn):
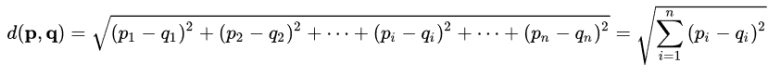
Bei jeder Beobachtung wird, um die Anzahl der Nachbarn in höchstens einer Entfernung ε zu zählen, die euklidische Entfernung zwischen dem Nachbarn und der Beobachtung berechnet und überprüft, ob diese kleiner als ε ist.
Bleibt nun noch die Frage, wie man das richtige Epsilon auswählt. Angenommen, wir entscheiden uns in unserem Beispiel dafür, den Algorithmus mit verschiedenen Werten von ε zu testen. Hier ist das Ergebnis :
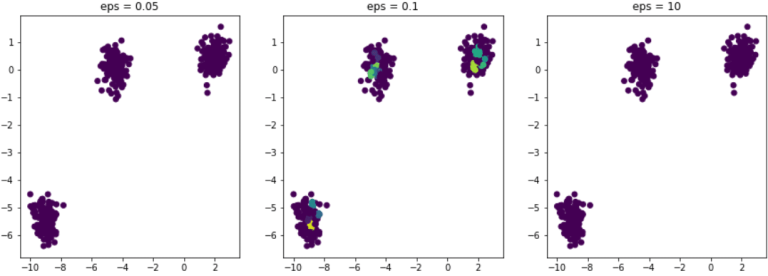
In allen drei Beispielen ist die minimale Anzahl an Nachbarn immer auf 5 festgelegt.
Wenn ε zu klein ist, ist die ε-Nachbarschaft zu gering und alle Beobachtungen im Datensatz werden als Anomalien betrachtet.
Dies ist der Fall in der linken Abbildung eps = 0,05.
Im Gegensatz dazu enthält jede Beobachtung, wenn epsilon zu groß ist, in ihrer ε-Nachbarschaft alle anderen Beobachtungen des Datensatzes. Folglich erhalten wir nur einen einzigen Cluster. Es ist daher sehr wichtig, das ε gut zu kalibrieren, um eine qualitativ hochwertige Partitionierung zu erhalten.
Eine einfache Methode, um ε zu optimieren, besteht darin, für jede Beobachtung zu schauen, wie weit ihr nächster Nachbar entfernt ist. Dann kannst du einfach ein ε so festlegen, dass ein „ausreichend großer“ Anteil der Beobachtungen einen Abstand zum nächsten Nachbarn hat, der kleiner als ε ist. Mit „ausreichend groß“ sind 90-95% der Beobachtungen gemeint, die mindestens einen Nachbarn in ihrer ε-Nachbarschaft haben müssen.
Wie implementiert man DBSCAN mit Python?
Das Training von DBSCAN wird durch die Scikit-Learn-Bibliothek erleichtert. Unser Datensatz, der als Beispiel diente, lässt sich leicht mit der Funktion make_blobs von Scikit-Learn erstellen. Hier ist, wie sie in Code implementiert wird :
Da wir nun unseren Datensatz haben, werden wir versuchen, das optimale ε zu bestimmen, um eine bessere Partitionierung unseres Datensatzes zu erreichen.
Scikit-Learn stellt eine Klasse NearestNeighbors zur Verfügung, mit der die nächsten Nachbarn jeder Beobachtung sowie die Entfernungen ermittelt werden können. Hier ist, wie man sie in Code implementiert:
Hier ist das Ergebnis:
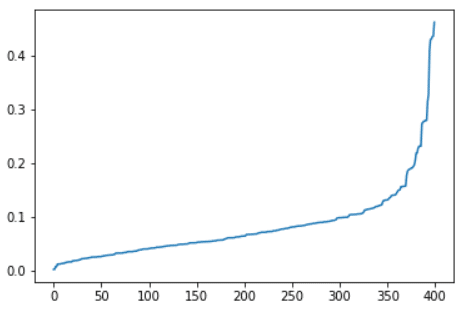
Wie wir zuvor gesehen haben, werden wir ein ε so wählen, dass 90% der Beobachtungen einen Abstand zum nächsten Nachbarn haben, der kleiner als ε ist. In unserem Beispiel scheint 0,2 geeignet zu sein.
Nun, da wir unser ε optimiert haben, können wir unsere Partitionierung mithilfe von DBSCAN durchführen, das bereits in Scikit-Learn implementiert ist.
Hier ist das Ergebnis:
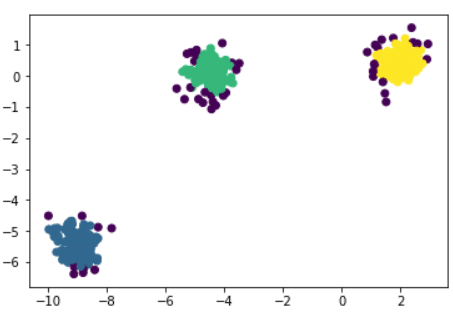
Mit den Argumenten eps und min_samples können die Parameter des Algorithmus festgelegt werden, nämlich der Abstand ε und die minimale Anzahl von Nachbarn, um als Kernbeobachtung zu gelten.
Der Algorithmus hat also 3 Hauptcluster und einige Anomalien entdeckt. Jede der Beobachtungen wird mit dem Label des entsprechenden Clusters beschriftet (z. B. 0,1,2). Die Anomalien werden mit -1 beschriftet und bilden somit eine eigene Klasse zusätzlich zu den 3 entdeckten Clustern.
Die Verwendung eines Clustering-Algorithmus wie DBSCAN ist nicht einfach, je nachdem, welche Daten du hast. Die Daten müssen oftmals nachbearbeitet werden.
Hat dir diese Serie über Clustering gefallen? In den DataScientest-Schulungen lernst du, alle wichtigen Clustering-Algorithmen zu beherrschen und sie in Datensätzen zu interpretieren.