Die Qualität der Leistung des maschinellen Lernens hängt in hohem Maße von den verfügbaren Informationen ab. Deshalb müssen Data Scientists die verwendeten Datensätze genau untersuchen. Dazu steht ihnen eine Vielzahl von statistischen Werkzeugen zur Verfügung. Eines davon ist die Kurtosis. Worum geht es also? Wozu dient sie? Hier findest du die Antworten.
Was ist Kurtosis?
Abgeleitet vom altgriechischen Namen κύρτωσις (bedeutet Krümmung) ist die Kurtosis ein statistisches Instrument zur Messung der Schärfe und Abflachung der Verteilung eines echten Zufallswerts.
Die Abflachung entspricht der Wahrscheinlichkeit und/oder Häufigkeit des Auftretens von Ausreißern (d. h. extrem hohen oder extrem niedrigen Werten im Vergleich zum Durchschnitt). In einer Kurve stellt dies die Enden auf beiden Seiten einer Verteilung dar.
Gut zu wissen: Man spricht auch von Schärfekoeffizient, Abflachungskoeffizient und Beulungsgrad.
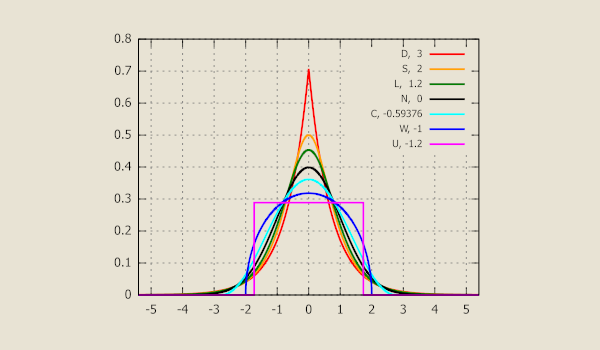
Welche Arten von Kurtosis gibt es?
Je nach dem Grad der Abflachung können die Verteilungen in drei Kategorien eingeteilt werden.
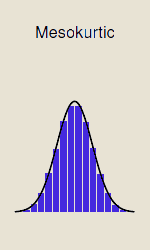
Mesokurtische Verteilungen
Dies sind die Verteilungen mit mittlerer Abflachung. Mit anderen Worten: Ausreißer sind weder sehr häufig noch sehr selten.
Die Kurtosis wird immer im Verhältnis zu einer Normalverteilung gemessen. Grundsätzlich hat die Normalverteilung eine Kurtosis von 3. Wenn dies der Fall ist, werden alle Verteilungen mit einer ähnlichen Kurtosis als mesokurtisch betrachtet.
Gut zu wissen: Oft wird die Kurtosis durch eine überschüssige Kurtosis beschrieben, d.h. -3. Diese überschüssige Abflachung erleichtert den Vergleich von Verteilungen mit der Norm. Auch hier gilt, dass alle Verteilungen mit einer Kurtosis nahe 0 als mesokurtisch angesehen werden.
Diese Art von Verteilung betrifft z. B. das Geburtsgewicht von Babys. Selbst wenn es Ausreißer gibt (5 oder 2 Kilogramm bei der Geburt), kommen sie weder sehr häufig noch sehr selten vor.
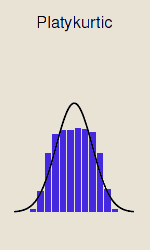
Die platykurtischen Verteilungen
Dies sind die Verteilungen mit geringer Abflachung (das sind die dünnen Schwänze). Das bedeutet, dass Ausreißer nur sehr selten vorkommen.
In diesem Fall ist die Kurtosis niedriger als bei einer Normalverteilung. Sie ist kleiner als 3 und die Exzess-Kurtosis kleiner als 0. Daher spricht man auch von negativer Verflachung, da der Exzess der Verflachung negativ ist.
Wissenswertes: Der Name PlatyKurtosis (und genauer gesagt der Begriff platy) stammt vom griechischen Wort platús, was flach bedeutet. Dies erklärt sich, da viele Platykurtische Verteilungen eine abgeflachte Spitze haben, obwohl einige auch spitz sein können. Aber Vorsicht: Die Kurtosis misst die Länge der Abflachung (die beiden Enden der Verteilung), nicht den „Peak“. PlatyKurtosis kommt also von einer Verwechslung der damaligen Statistiker, aber der Begriff ist geblieben.
Auf einer Kurve wird eine platykurtische Verteilung normalerweise in eine Gleichverteilung übersetzt. Es gibt fast keine Abweichungen zwischen den einzelnen Variablen.
Das wäre zum Beispiel der Fall bei einer Studie über die Nutzung von sozialen Netzwerken durch Oberschüler. Hier sind sie fast alle gleich alt und nutzen ebenfalls fast alle sozialen Medien, unabhängig von ihrem Alter. Es gibt keine oder nur wenige Ausreißer (innerhalb einer High School wären nur wenige Schüler älter als 18 oder jünger als 14 Jahre).
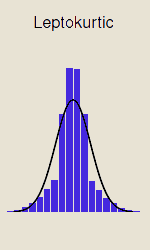
Leptokurtische Verteilungen
Dies sind die Verteilungen mit einer hohen Abflachung. Mit anderen Worten: Es gibt viele Ausreißer. Diese sind daher höher als bei einer Normalverteilung. Dies äußert sich in einer Kurtosis von mehr als 3 und einer Excess Kurtosis von mehr als 0. Hier spricht man von einer positiven Kurtosis.
Eine leptokurtische Verteilung könnte sich zum Beispiel auf die Entfernung der Erde zu anderen Sternen im Universum beziehen. Einige sind relativ nah (oder zumindest erreichbar), während andere Hunderte von Lichtjahren entfernt sind.
Wozu dient Kurtosis?
Die Kurtosis ist eines der wichtigsten statistischen Tool, da sie die Ungleichheit der Werte innerhalb einer Verteilung bestimmt. Sie kann in einer Vielzahl von Branchen angewendet werden.
Hier sind die häufigsten:
- Finanzanalyse: Mithilfe der Kurtosis kann das Risiko der Preisvolatilität einer Investition gemessen werden. Wenn die Kurtosis hoch ist (im Falle einer leptokurtischen Verteilung), bedeutet dies, dass die gewählte Investition gelegentlich extreme Renditen erwirtschaften wird. Dadurch können sich die Gewinne exponentiell vervielfachen, aber auch viel Geld verloren gehen. Umgekehrt deutet ein Aktienportfolio mit einem niedrigen Kurtosis-Wert auf eine stabilere und vorhersehbarere Rendite hin. Also weniger Risiko, aber auch weniger Gewinn.
- Machine Learning: Hier geht es darum, die Disparität eines Datasets zu messen. Dies bedeutet jedoch nicht, dass die verfügbaren Daten schlecht sind. Es geht vor allem darum, dass Data Scientists den Datensatz besser verstehen können, um die Leistung beim maschinellen Lernen zu verbessern.
Was sind die Unterschiede zwischen Skewness und Kurtosis?
Um die Disparität eines Datensatzes zu messen, können Data Scientists entweder die Kurtosis oder die Skewness verwenden. Im zweiten Fall geht es vor allem darum, die Verteilung um den Zentralwert zu messen. Im Gegensatz dazu misst die Kurtosis eher die Häufigkeit von Ausreißern.
In beiden Fällen handelt es sich jedoch um unverzichtbare Messinstrumente für das maschinelle Lernen.
Möchtest du mehr über Machine Learning erfahren?
Abgesehen von statistischen Werkzeugen erfordert Machine Learning verschiedene Kompetenzen in den Bereichen prädiktive Analyse, Computersprache, Datenbanken usw. Daher ist es mehr als notwendig, eine Ausbildung in Datenwissenschaft zu absolvieren. Aus diesem Grund bieten wir dir die Ausbildung zum Data Scientist an. Entdecke ihn!









