„Gemeinsam sind wir stärker“: Mit diesem Zitat könnte man Bootstrap aggregating (kurz Bagging genannt) definieren. Tatsächlich gehört diese Technik zu den Ensemblemethoden, bei denen eine Gruppe von Stichproben betrachtet wird, um die endgültige Entscheidung zu treffen. Nun schauen wir uns den Fall des Baggings genauer an.
Zunächst ist es notwendig, dass wir mit Daten arbeiten. Wir werden nämlich nicht alle unsere Modelle mit denselben Daten versorgen, damit unsere Modelle unabhängig voneinander bleiben. Das Problem dabei ist, dass wir den Datensatz nicht zerlegen können. Bei einer großen Anzahl von Modellen würden unsere Modelle nicht ausreichend trainiert und schlechte Ergebnisse liefern.
Bagging - Die Lösung unseres Problems: Bootstrap
Um dieses Problem zu lösen, erstellen wir einen Bootstrap-Datensatz. Bei dieser Methode erstellen wir einen neuen Datensatz aus dem ursprünglichen Datensatz. Der neue Datensatz hat die gleiche Größe wie der Ausgangsdatensatz. Bezeichnen wir n als Stichprobengröße und nennen wir E_1 den ursprünglichen Datensatz und E_2 den durch Bootstrap erstellten Datensatz. Aus E_1 wählen wir zufällig eine Person aus, die wir in E_2 platzieren. Diesen Schritt werden wir wiederholen, bis E_2 die Größe n hat. Es ist wichtig zu bemerken, dass die ausgewählten Elemente immer in E_1 sind, wir können das gleiche Element mehrmals auswählen. Mit dieser Besonderheit werden unterschiedliche Daten erzeugt.
Schauen wir uns zum besseren Verständnis ein konkretes Beispiel an, wobei wir die obigen Schreibweise übernehmen.
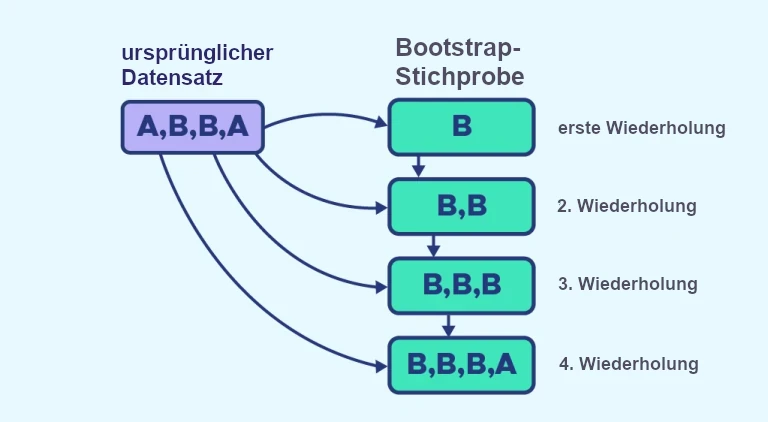
- Hier besteht E_1 aus 2 Elementen namens A und 2 Elementen namens B, E_2 ist leer und n=4.
- In der ersten Wiederholung wird zufällig ein Element aus E_1 ausgewählt, B wird in E_2 platziert.
- Dieser Vorgang wird wiederholt, bis E_2 aus 4 Elementen besteht.
- Schließlich besteht E_2 aus 3 Elementen B und einem Element A. Ein Element B wurde dreimal ausgewählt.
Nachdem wir nun gesehen haben, was Bootstrap ist, entscheiden wir uns dafür, 3 Bootstrap-Stichproben* zu nehmen. Jeder Stichprobe werden wir ein anderes Modell zuweisen. Es ist üblich, Entscheidungsbäume zu verwenden. Wir trainieren jedes Modell und machen unsere Vorhersagen.
*die Wahl von 3 ist willkürlich
Was können wir jetzt mit drei Vorhersagen anfangen?
Wir brauchen einen einzigen Wert für unser Problem, deshalb machen wir hier eine Datenaggregation. Für Klassifikationsmodelle werden wir ein Wahlsystem anwenden und für Regressionsmodelle werden wir den Mittelwert des vorhergesagten Wertes berechnen. Nach dem Ausgangszitat konstruieren wir aus mehreren Modellen ein endgültiges Modell.
Ein Beispiel für ein Wahlsystem, bei dem wir A oder B vorhersagen müssen, können wir mit dem folgenden Beispiel sehen:
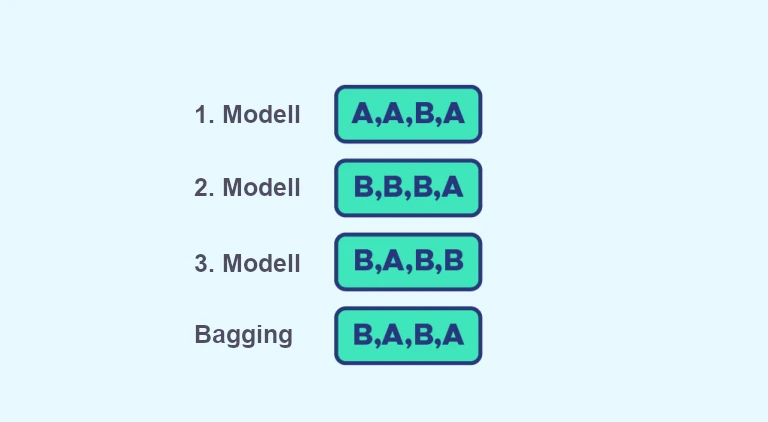
Um uns zu merken, was Bagging ist, können wir uns daran erinnern, dass es sich um eine Kombination aus Bootstrap und Aggregation handelt. Ein bekannter Bagging-Algorithmus ist der berühmte Random Forest. Außerdem kannst Du Dich in diesem Artikel über eine weitere bekannte Aggregationstechnik, das Boosting, informieren.
Bagging = Bootstrap + Aggregating
Eine der Stärken dieser Methode ist die Verringerung der Varianz, denn auch wenn die Modelle nicht mit demselben Datensatz trainiert werden, teilen die Bootstrap-Stichproben gemeinsame Tupel, was zu einer Verzerrung führt. Diese erzeugte Verzerrung führt zu einer Verringerung der Varianz.
Ein zweiter Vorteil ist die Korrektur von Fehlvorhersagen. Betrachten wir das untere Bild. Jedes Modell macht einen Fehler bei der Vorhersage der Klassifizierung, aber jeder Fehler wird durch das Wahlsystem korrigiert.
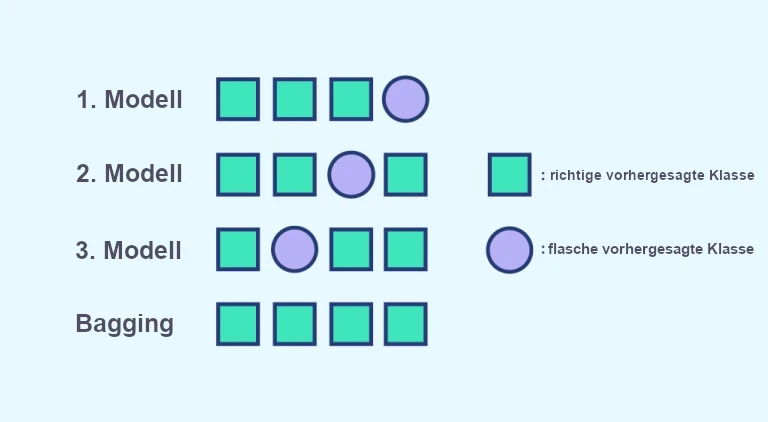
Wir haben gesehen, wie Bagging mit Ensemblemethoden zusammenhängt. Wie in der Einleitung erwähnt, verwenden wir mehrere Modelle, deren Vorhersagen wir zu einer endgültigen Vorhersage aggregieren. Um unsere verschiedenen Modelle zu kalibrieren, erstellen wir verschiedene Datensätze durch Bootstrapping auf die Ausgangsstichprobe.
Wenn Du dies in die Praxis umsetzen möchtest, kannst Du Dich gerne für unsere Weiterbildung zum/r Data Scientist anmelden.