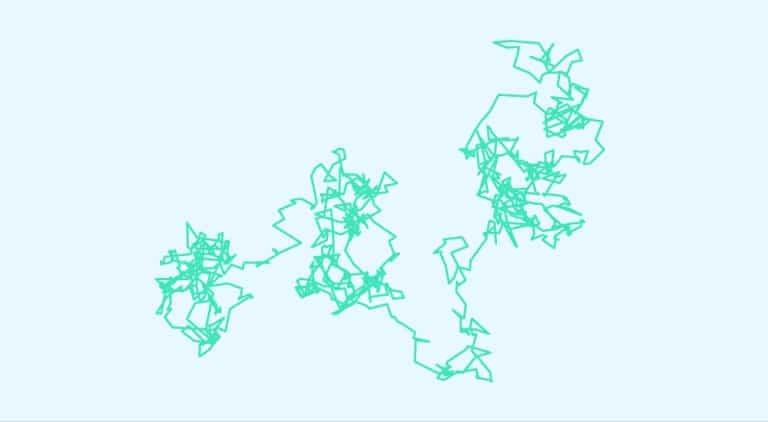
Nehmen wir ein mikrometergroßes Teilchen, das in einer Flüssigkeit schwimmt. Andere kleinere Teilchen stoßen auf dieses „größere“ Teilchen, sodass es eine zufällige Bewegung hat. Das Prinzip der Brownschen Bewegung wird auch als Wiener-Prozess bezeichnet.
Historisch gesehen entdeckte der Botaniker Robert Brown die Brownsche Bewegung im Jahr 1827. Er beobachtete die chaotische Bewegung von Pollenkörnern in Wasser.
Ab 1857 interessierten sich mehrere Wissenschaftler für Robert Browns und definierten die Eigenschaften der Brownschen Bewegung.
Erst im Jahr 1905 beschreibt Albert Einstein quantitativ die Brownsche Bewegung. Er verknüpft insbesondere den quadratischen Mittelwert der zurückgelegten Strecke mit der Dauer der Beobachtung. Seine Berechnungen sind von Jean Perrin experimentell bestätigt. Seine Experimente ermöglichten es ihm auch, die Avogadro-Konstante zu bestimmen.
Die Brownsche Bewegung findet in verschiedenen Bereichen Anwendung. In dem Bereich der Physik verwendet man sie, um Bewegungen kleiner Partikel, wie z. B. Aerosole in der Luft, zu bestimmen. Dabei wird eine Zufallskraft berücksichtigt (z. B. in den Langevin-Gleichungen).
Diese hat auch mathematische Anwendungen in Form von stochastischen Prozessen: probabilistische Modelle, mit denen ein zufälliges Phänomen im Laufe der Zeit untersucht werden kann. Sie wird häufig in der Wahrscheinlichkeitsrechnung verwendet, und es gibt mehrere Anwendungen im Finanzbereich.
Die Anwendung der Brownschen Bewegung bei der Mikromanipulation von DNA-Molekülen
1. Das Prinzip
Als Beispiel nehmen wir eine der physikalischen Anwendungen der Brownschen Bewegung, nämlich die Mikromanipulation von DNA-Molekülen. Die Mikromanipulation von DNA-Molekülen kann mithilfe verschiedener Werkzeuge wie optischer oder magnetischer Pinzetten durchgeführt werden.
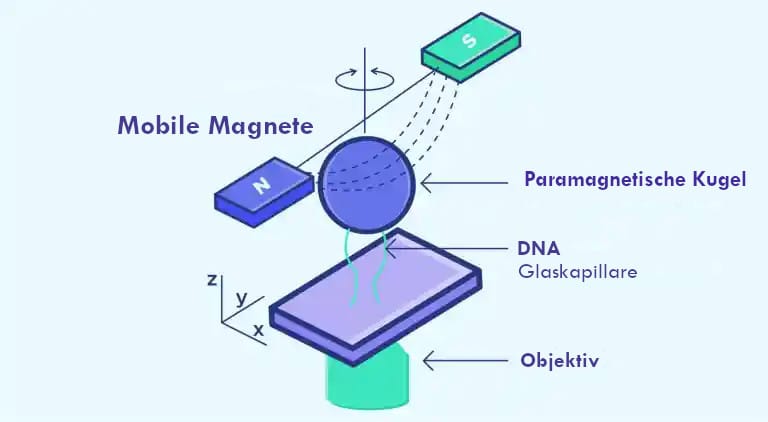
Das Prinzip der Mikromanipulation funktioniert wie folgt:
- Ein Ende des DNA-Moleküls wird an einer Glaskapillare befestigt.
- Am anderen Ende wird eine magnetische Kugel befestigt. Diese Kugel wird in das Feld eines Magnetes gebracht.
- Durch die Bewegung des Magnetes wird das DNA-Molekül entweder gezogen oder um die eigene Achse gedreht, um Verdrillungen zu erzeugen.
2. Bedeutung der Brownschen Bewegung
Nun können wir uns fragen: Wo kommt die Brownsche Bewegung ins Spiel?
Die Kraft, die nötig ist, um das DNA-Molekül zu strecken, liefert ziemlich wichtige Informationen über unser Makromolekül.
Diese Kraft ist sehr schwach (im Bereich von Pikonewton, d. h. 10-12 Newton). Da sie so schwach ist, kann sie nicht leicht mit herkömmlichen Messgeräten gemessen werden, da diese durch die thermische Bewegung eingeschränkt sind.
Die Brownsche Bewegung ermöglicht es jedoch, Kraft zu messen. Die thermische Bewegung erzeugt eine zufällige Kraft, die die Kugel aus ihrer Gleichgewichtslage bringt. Anhand von Berechnungen lässt sich zeigen, dass die Streckkraft des DNA-Moleküls direkt mit den mittleren quadratischen Abweichungen zusammenhängt.
Nun müssen wir noch die mittleren quadratischen Abweichungen bestimmen. Hierzu sollten wir uns von Jean Perrins Experiment inspirieren lassen.
- Ein erster Schritt besteht darin, die Bewegungen des kugelförmigen Teilchens, das sich am Ende des DNA-Moleküls befindet, mit einer an ein Mikroskop angeschlossenen Kamera aufzuzeichnen.
- In einem zweiten Schritt werden mithilfe von Videoerkennungssoftwares die Koordinaten des Kügelchens zu jedem Zeitpunkt abgerufen. Dann lassen sich anhand der Koordinaten die Brownschen Abweichungen berechnen.
💡 Auch interessant:
3. Verwendung von Python, um auf die Koordinaten der Kugel zuzugreifen
Ausgehend vom Video können wir mithilfe von Python auf viel komplexere Weise auf die Koordinaten der Kugel zugreifen.
Sobald das Video in eine Folge von Einzelbildern umgewandelt wurde, verwenden wir die imageio-Bibliothek von Python.
Somit kann man mit Bildern arbeiten, weil diese Bibliothek Bilder als dreidimensionale Arrays darstellt.
In den ersten beiden Dimensionen können wir die Position eines Pixels bestimmen und die dritte Dimension gibt uns Auskunft über die Farbintensität (woraus wir die Farbe des Pixels ableiten können).
Sobald die Bilder in Graustufen umgewandelt wurden, können wir uns auf eine zweidimensionale Tabelle zurückziehen, da die Werte in der dritten Dimension alle gleich sind (da das Bild in Graustufen vorliegt). Wir müssen dann nur noch Funktionen erstellen, die es uns ermöglichen, die Koordinaten des Pixels mit der höchsten Intensität mithilfe einer baryzentrischen Methode zu bestimmen. Wenn wir diesen Vorgang über die Folge von Bildern wiederholen, erhalten wir am Ende unsere Koordinaten der Kugel zu jedem Zeitpunkt.
Der Zugriff auf die Koordinaten ermöglicht den Zugriff auf die Brownschen Abweichungen und dann auf die Streckkraft des DNA-Moleküls.
Somit ist die Brownsche Bewegung sehr nützlich bei der Mikromanipulation des DNA-Moleküls. Die Arbeit mit der Videoanalyse ist ebenfalls ein sehr wichtiger Aspekt. Wie wir gesehen haben, kann dieser Prozess mit Hilfe von Python durchgeführt werden.
Mit den von DataScientest angebotenen Kursen kannst Du lernen, Python zu beherrschen, nämlich ein unverzichtbares Werkzeug in der Datenwissenschaft. Wir bieten auch eine Lerneinheit zur Bildverarbeitung an: Einführung in Computer Vision mit OpenCV.
Über den Autor…
Avraham Rosenberg studiert an einer Ingenieurschule sowie an der Universität Paris-Saclay und spezialisiert sich auf angewandte Mathematik im Bereich Data Science sowie künstliche Intelligenz.