Die Anzahl der "expected goals" ist ein neuer Leistungsindikator, der erst vor kurzem in der Fußballanalyse aufgetaucht ist. Diese Statistik wird immer häufiger verwendet, um die Physiognomie eines Spiels zu interpretieren, aber wissen wir wirklich, wie sie zu interpretieren ist?
Dieser Artikel soll dir so einfach wie möglich die mathematischen Konzepte hinter den expected goals (xG) näher bringen. Die Ergebnisse stammen aus einer Simulation, die David Sumpter auf dem Youtube-Kanal Friends of Tracking mit Daten der Premier League über eine ganze Saison durchgeführt hat.
Was ist ein Expected Goal?
Was ist ein xG? Was bedeutet ein Ergebnis von 2,71 zu 0,78 in xG ?
Jedem Schuss, der in einem Spiel abgegeben wird, kann eine Wahrscheinlichkeit zugeordnet werden, dass der Ball im Tor landet.
Beispielsweise hat ein Schuss aus 35 Metern eine sehr geringe Erfolgswahrscheinlichkeit (vielleicht 5%, also 0,05 xG), während ein Schuss nach einem Elfmeter eine gute Chance hat, den Torwart zu überlisten (76%, also 0,76 xG). Wenn wir die Expected Goals aller Schüsse in einem Spiel addieren, erhalten wir also eine Punktzahl in xG..
Im Vergleich zum klassischen Score, der nur die Tore zählt, haben xG den Vorteil, dass sie über eine größere Anzahl von Ereignissen berechnet werden. Daher spiegeln sie oft den Charakter eines Spiels wider und lassen erkennen, welche Mannschaft die meisten Chancen hatte..
Aber wie wird diese Wahrscheinlichkeit dann berechnet?
Um dies zu verstehen, wollen wir ein einfaches Modell für erwartbare Tore erstellen. Wir gehen von folgender Intuition aus: Je weiter du vom Tor entfernt bist, desto schwieriger wird es, ein Tor zu erzielen. In unserem Modell wird die Wahrscheinlichkeit eines Treffers nur anhand der Position des Schusses ermittelt. .
Wir werden also die Verteilung der Schüsse im zweidimensionalen Raum visualisieren..
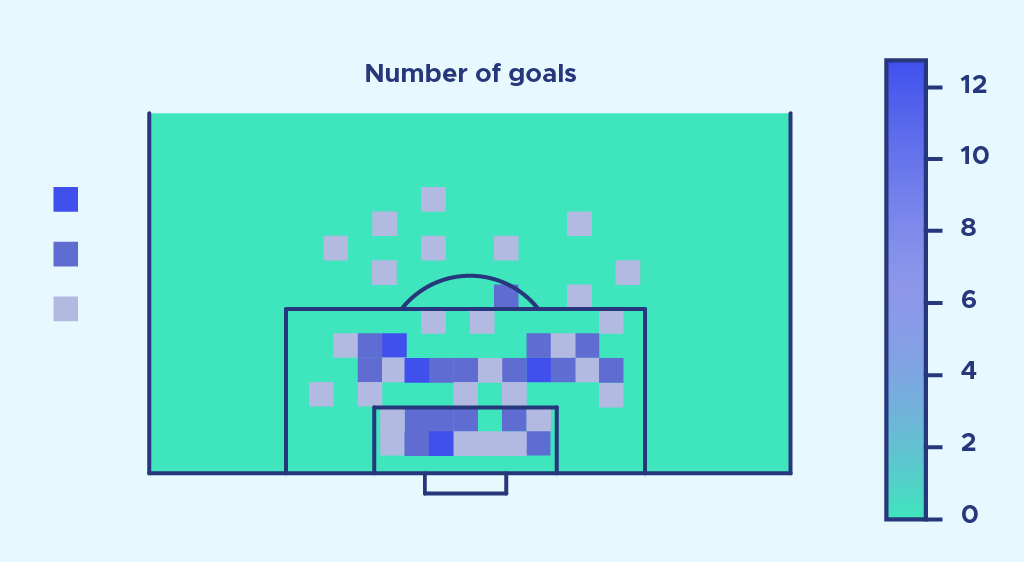
So sieht eine komplette Fußballsaison in der ersten Liga aus:.
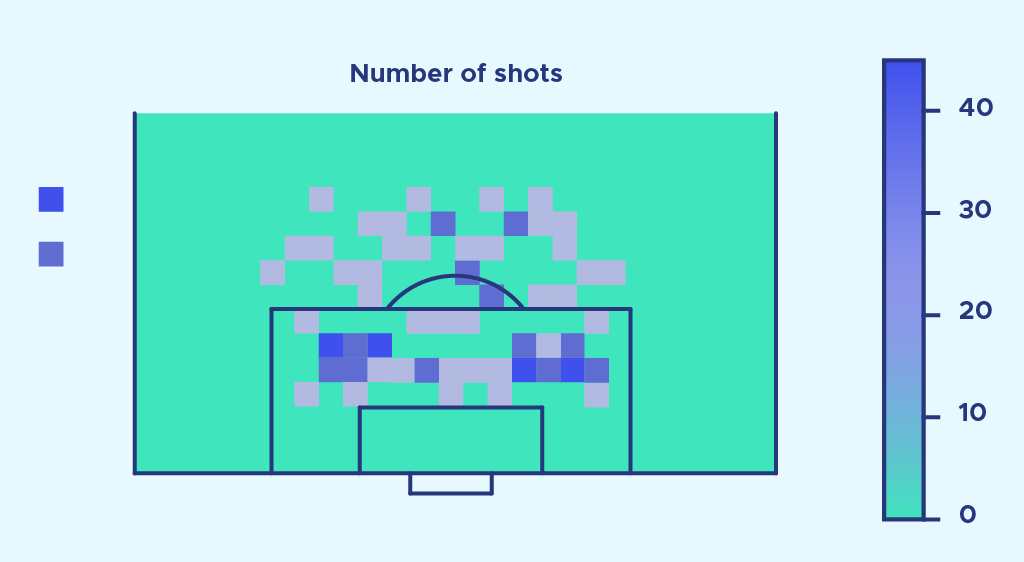
Nun vergleichen wir mit der Verteilung der erzielten Tore:
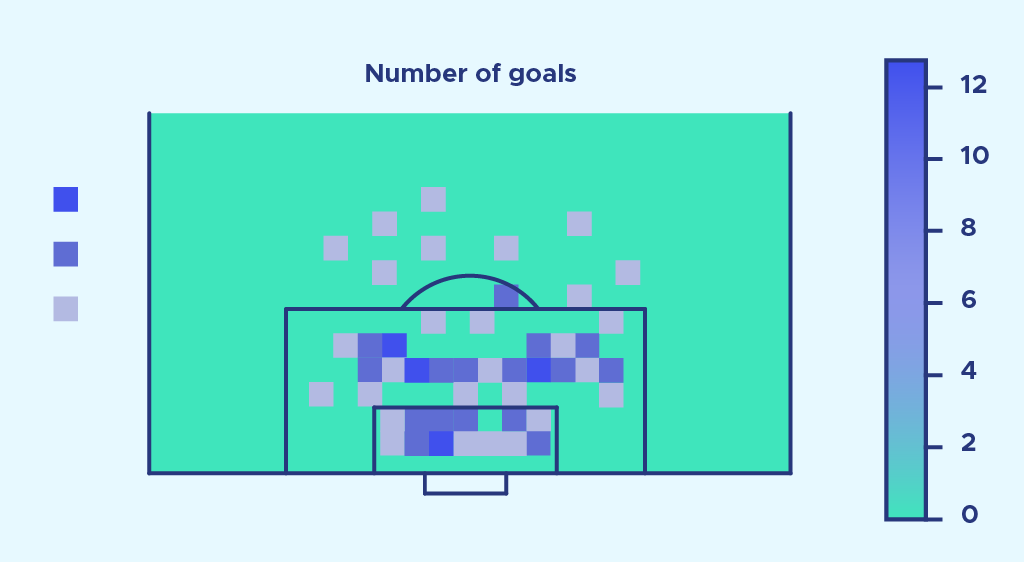
Es fällt auf, dass die Anzahl der Schüsse außerhalb des Strafraums proportional viel höher zu sein scheint als die Anzahl der Tore.
Nun erinnern wir uns daran, dass unser Ziel darin besteht, die Wahrscheinlichkeit eines Tores für jeden Schuss zu ermitteln. Um dies zu erreichen, setzen wir das Verhältnis Anzahl der Tore/Anzahl der Schüsse Anzahl der Tore Anzahl der Schüsse für jeden Rasterbereich des Raumes. Dieses Verhältnis ist unsere Wahrscheinlichkeit, ein Tor zu erzielen. Dann zeigen wir diese Wahrscheinlichkeit für jeden Bereich des Raumes an und das Ergebnis sieht so aus:
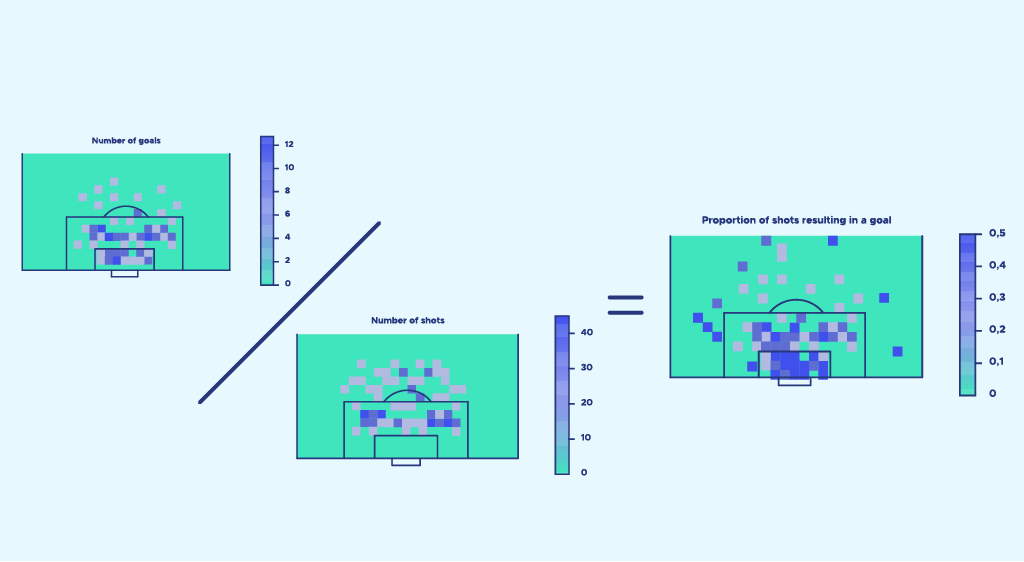
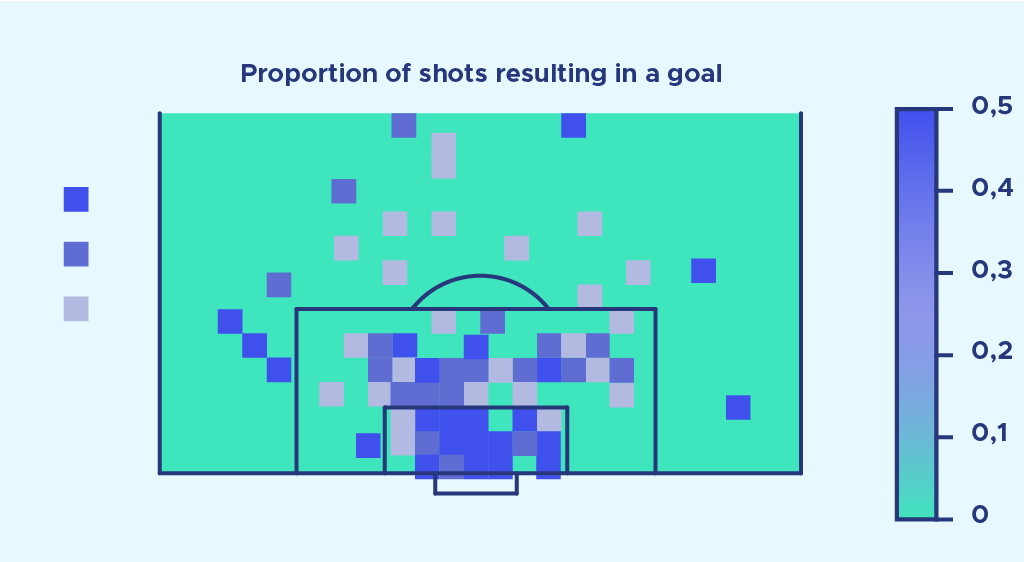
Dieses Bild ist eine erste Vorlage für Expected Goals. Aber wie du sehen kannst, ist es alles andere als perfekt und hat viele Einschränkungen.
Die erste Beobachtung, die wir machen können, ist, dass das Ergebnis einige Anomalien zu haben scheint.
In der Tat scheinen einige sehr weit entfernte Bereiche des Raumes eine sehr hohe Markierungswahrscheinlichkeit zu haben..
Dies liegt daran, dass das Beispiel nur Schüsse aus einer einzigen Saisonin einer einzigen Liga berücksichtigt. Manchmal gab es nur einen Schuss in einer sehr weit entfernten Zone, und dieser Schuss wurde getroffen, und das ist es, was wir die Magie des Fußballs nennen. Hätten wir unsere Berechnungen jedoch mit viel mehr Daten durchgeführt (mehrere Ligen über mehrere Saisons), hätte das erzielte Ergebnis weniger starke Anomalien aufgewiesen..
Ausgehend von dieser erzeugten Visualisierung versuchen wir nun, ein mathematisches Modell zu erstellen, das am besten zu der beobachteten Torhäufigkeit passt. Dazu werden wir zwei Parameter separat untersuchen: den Schusswinkel und die Entfernung zum Tor.
Der Schusswinkel ist der Winkel zwischen den beiden Pfosten an der Stelle des Schusses.
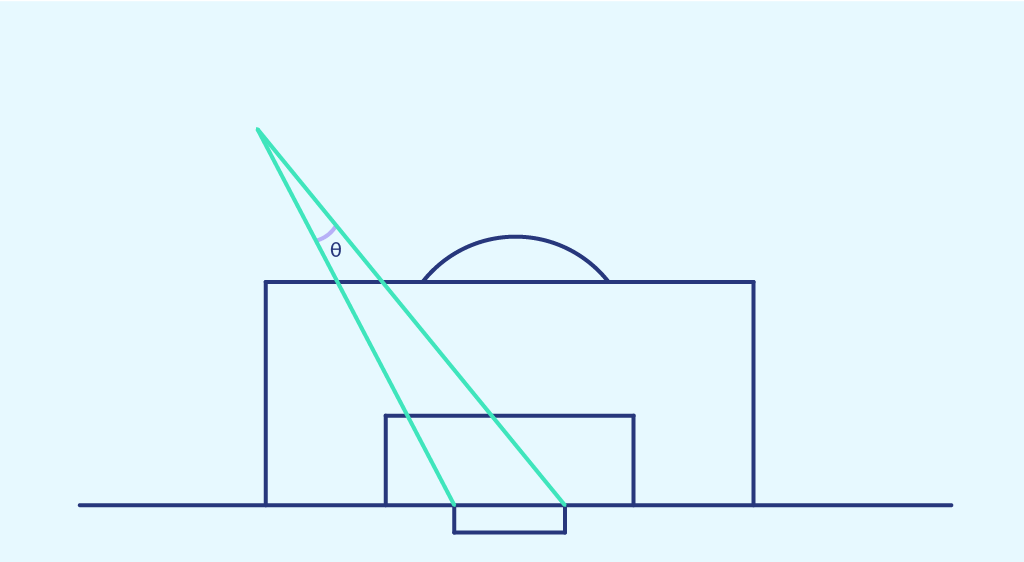
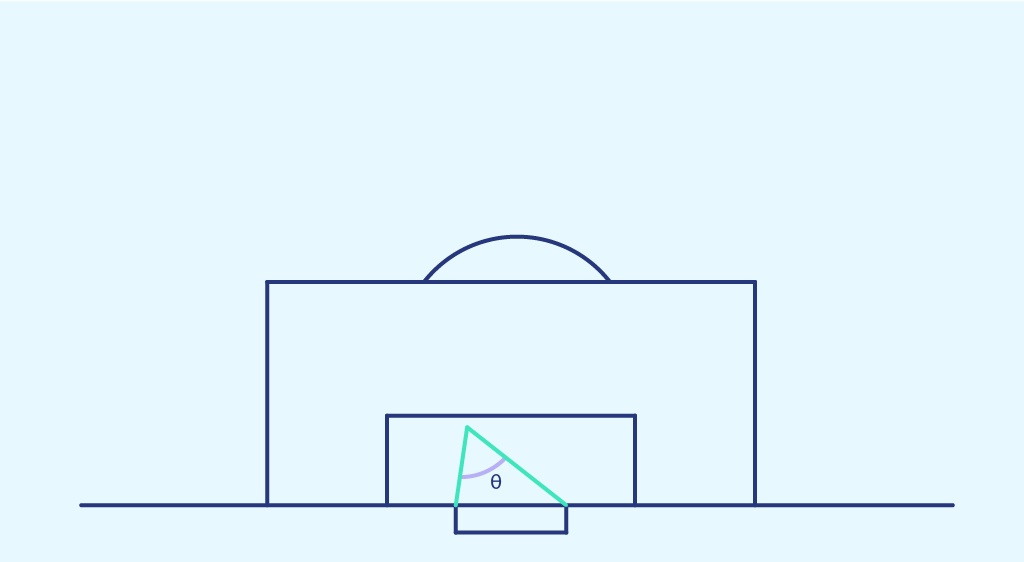
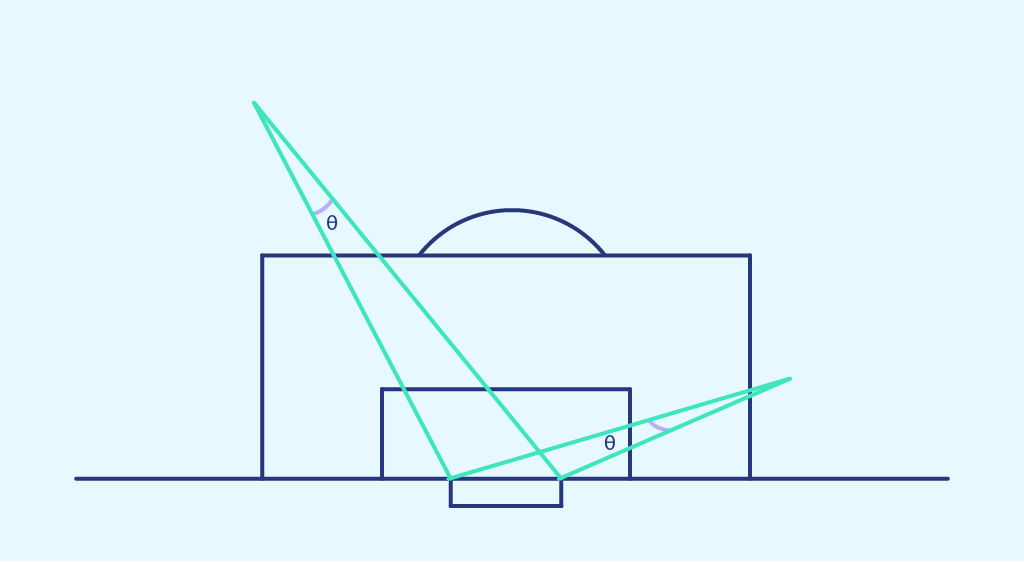
Diesmal stellen wir die Wahrscheinlichkeit eines Trefferser, die wir zuvor in jedem Bereich des Raumes erhalten haben, als Funktion des Schusswinkels dieses Bereiches dar. Das Ergebnis ist die folgende Punktwolke:
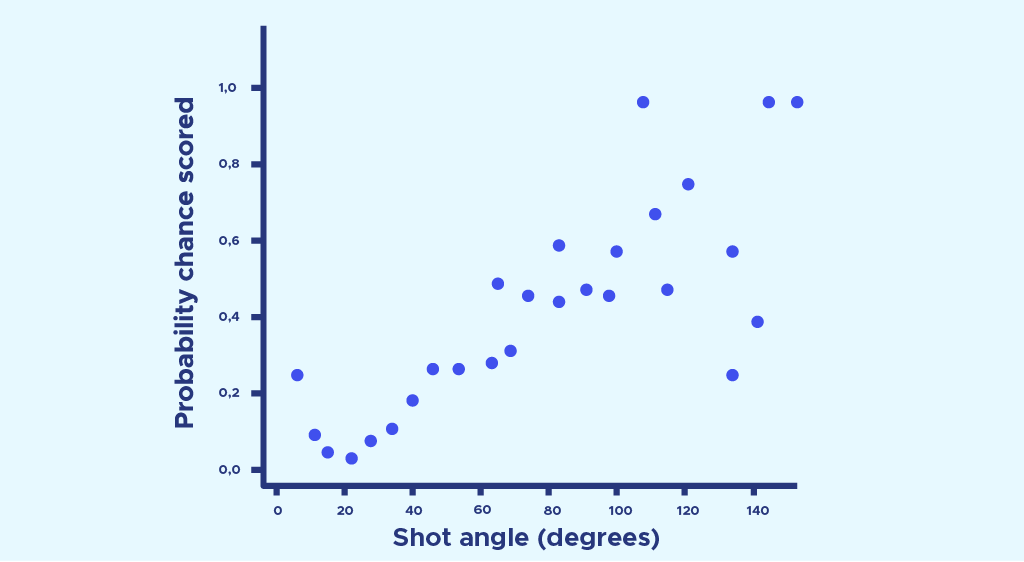
Anschließend wird eine logistische Regression durchgeführt, um diese Punkte mit der Formel P(theta) = . Wir haben uns für eine logistische Regression und nicht für eine lineare Regression entschieden, weil sie eine Trefferwahrscheinlichkeit von 1 hat, wenn sich der Winkel 180° nähert, und 0, wenn der Winkel 0° beträgt. (Eine kleine Auffrischung der logistischen Regression findest du in diesem Artikel).
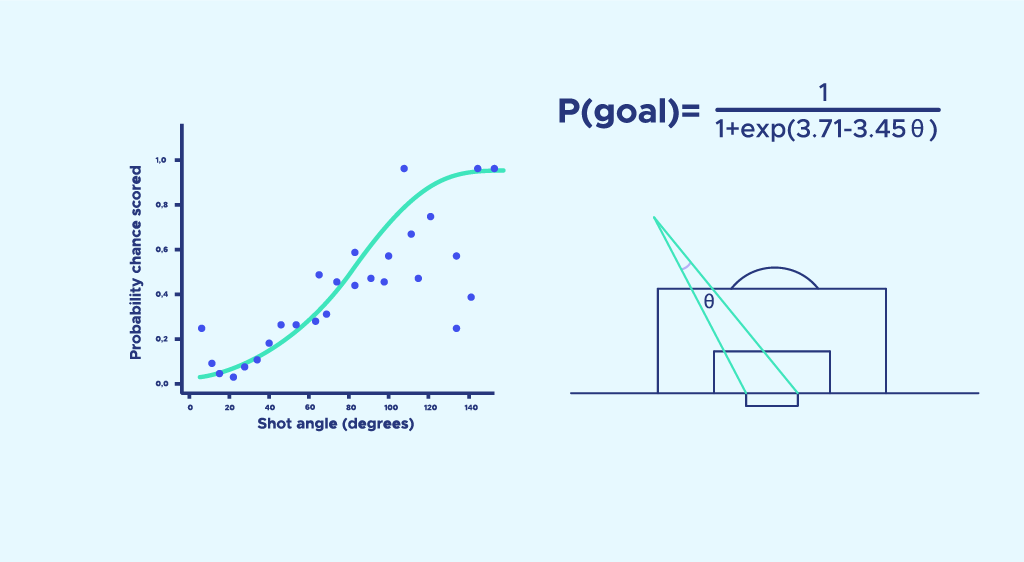
Nun können wir genau das gleiche mit der Distanz machen:
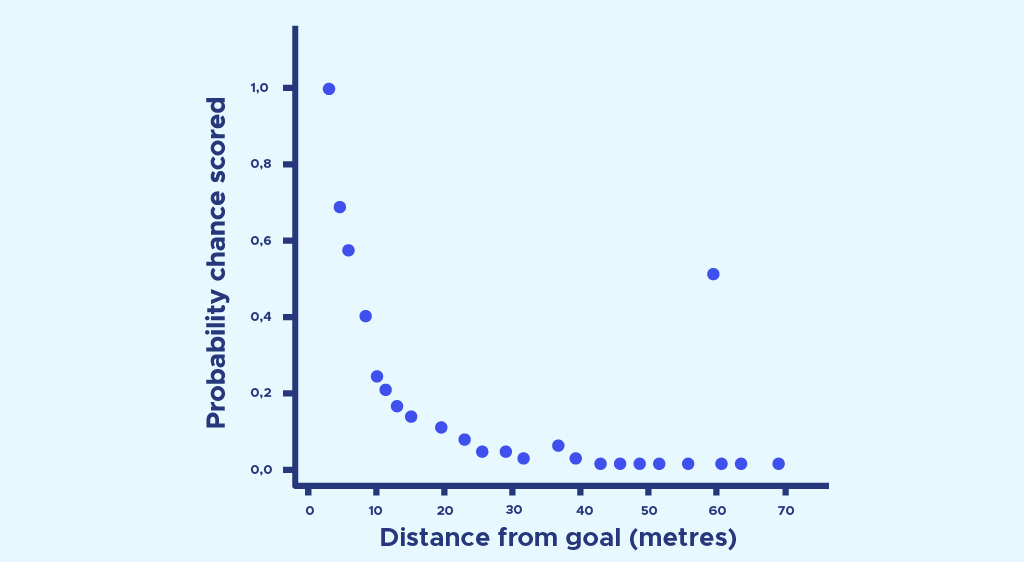
Auch hier führen wir eine logistische Regression durch und erhalten die Wahrscheinlichkeit eines Treffers in Abhängigkeit von der Entfernung :
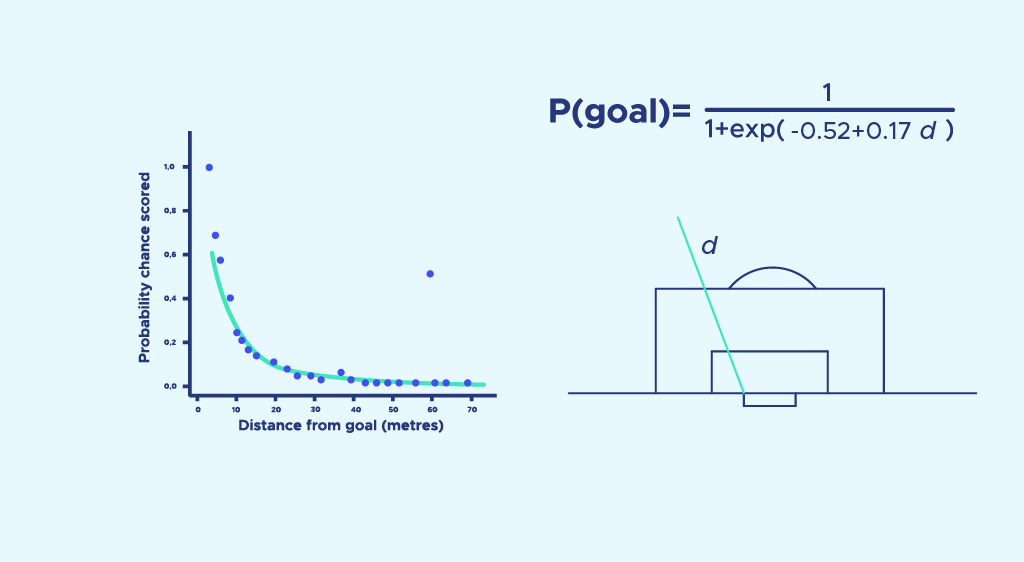
Das Modell ist nicht ideal, da die Wahrscheinlichkeit, aus 0 Metern Entfernung zu treffen, 1 betragen sollte. Es sollte verbessert werden (z. B. durch Hinzufügen von d2 in die Exponentialfunktion), aber wir gehen von dieser ersten Näherung aus.
Diese beiden mathematischen Modelle, eines auf der Grundlage des Winkels und das andere auf der Grundlage der Entfernung, sagen unsere experimentelle Trefferwahrscheinlichkeit ziemlich korrekt voraus. Dennoch tun sie dies nicht sehr genau.
Um die Genauigkeit unseres mathematischen Modells zu verbessern, berücksichtigen wir dieses Mal die Auswirkungen beider Dimensionen gleichzeitig.
Wir tun dies mithilfe einer multivariaten Regression, aber das würde den theoretischen Rahmen dieses Artikels sprengen. Das Ergebnis dieser bivariaten Regression ist wie folgt:
Das Modell ist nicht ideal, da die Wahrscheinlichkeit, aus 0 Metern Entfernung zu treffen, 1 betragen sollte. Es sollte verbessert werden (z. B. durch Hinzufügen von d2 in die Exponentialfunktion), aber wir gehen von dieser ersten Näherung aus.
Diese beiden mathematischen Modelle, eines auf der Grundlage des Winkels und das andere auf der Grundlage der Entfernung, sagen unsere experimentelle Trefferwahrscheinlichkeit ziemlich korrekt voraus. Dennoch tun sie dies nicht sehr genau.
Um die Genauigkeit unseres mathematischen Modells zu verbessern, berücksichtigen wir dieses Mal die Auswirkungen beider Dimensionen gleichzeitig.
Wir tun dies mithilfe einer multivariaten Regression, aber das würde den theoretischen Rahmen dieses Artikels sprengen. Das Ergebnis dieser bivariaten Regression ist wie folgt:
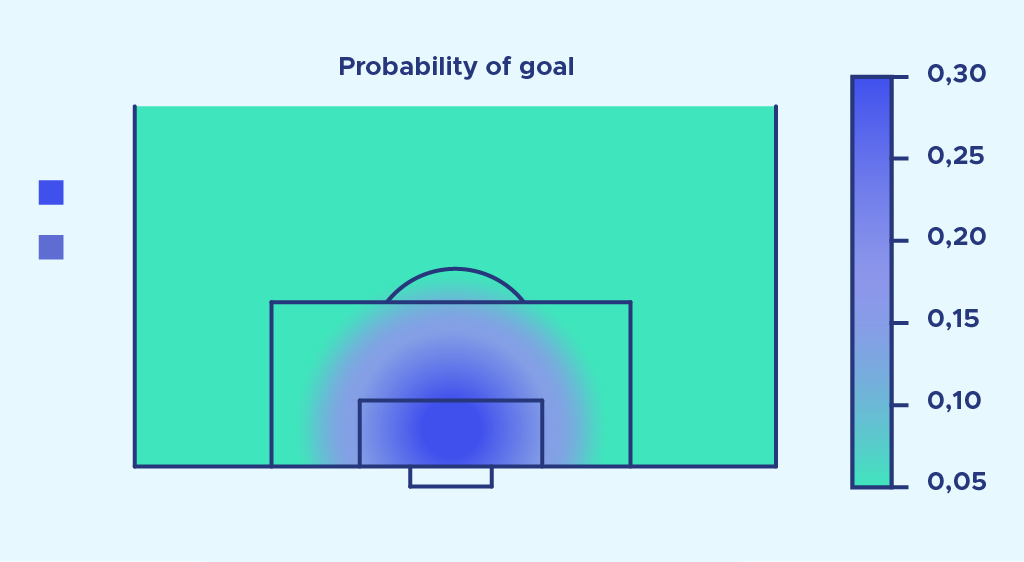
Dieses mathematische Modell berücksichtigt sowohl den Winkel als auch die Entfernung zum Ziel des Schusses. Es wurde so entwickelt, dass es der Realität der beobachteten Tore am besten entspricht. Daher ist das Modell jetzt viel allgemeiner, weist weniger Anomalien auf und scheint der Realität näher zu kommen. Auf der Grundlage dieses Modells ist es möglich, den nächsten Schüssen eine Trefferwahrscheinlichkeit zuzuordnen, je nachdem, wo der Schuss abgegeben wurde.
Fazit
Du hast gesehen, wie man aus dem Winkel und der Entfernung ein Modell für erwartete Tore erstellt. Dieses Modell ermöglicht es, erste Erkenntnisse für die Spieler zu gewinnen. Man erkennt z. B., dass es schwierig ist, ein Tor zu erzielen, wenn der Schuss exzentrisch ist, und dass ein Rückpass vielleicht besser geeignet ist.
Außerdem ist unser Modell alles andere als perfekt. Sein erster Fehler ist, dass es auf den Daten einer einzigen Meisterschaft in einer einzigen Saison basiert. Der zweite Nachteil ist, dass wir bei der Erstellung nur den Winkel und die Entfernung berücksichtigt haben. In besseren Modellen würden wir die Kontaktzone des Schusses (Kopf oder Fuß), die Position der Verteidiger zum Zeitpunkt des Schusses, die Art der Aktion (platzierter Angriff, Gegenangriff), die Wahl des Fußes (richtig oder falsch) und viele andere Parameter berücksichtigen.
Wenn es eine Sache gibt, die man aus diesem Artikel lernen kann, ist es, dass die expected goals konstruiert werden, um die Häufigkeit von Toren, die in Abhängigkeit von einer Vielzahl von Parametern beobachtet werden, bestmöglich zu passen. Eine Scoring-Wahrscheinlichkeit bleibt eine Wahrscheinlichkeit. Sie wird sich im Durchschnitt langfristig bewahrheiten, wenn sie richtig aufgebaut wird, aber in einem einzigen Spiel bleibt alles möglich und das ist es, was die Magie dieses Sports ausmacht.